$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}}$
今回は、観測データを大きさ順に並びかえた「順序統計量」を扱います。
「順序統計量」というワードは初めて聞きました。
あまり聞きなれないワードかも知れませんね。
順序統計量の確率密度関数の導出までを扱いますが、これを自力でできるようにしてください。
なんだかあまり自信がないですね。。
パターンはある程度決まっているので、あまり気負わずに取り組んでください。
1. 順序統計量とは
(定義)
$X_i \overset{i.i.d}\sim F ~ \small{(i=1, \ldots, n)}$である時、$X_i ~ \small{(i=1, \ldots, n)}$を大きさ順に並びかえたものを、
$$\begin{aligned} X_{(1)} \lt X_{(2)} \lt \cdots \lt X_{(n)} \end{aligned}$$と表し、$X_{(i)} ~ \small{(i=1, \ldots, n)}$を「順序統計量」と言います。
2. 順序統計量の確率密度関数
$X_i \overset{i.i.d}\sim F ~ \small{(i=1, \ldots, n)}$である時(ただし、分布$F$の確率密度関数を$f(x)$、分布関数を$F(x)$とします)、下から$k$番目の値$X_{(k)}$の確率密度関数$f_{(k)} (x)$は、
$$\begin{aligned} f_{(k)}(x) = \frac{n!}{(k-1)!(n-k)!} \cdot f(x) \cdot \{ F(x) \}^{k-1} \cdot \{ 1-F(x) \}^{n-k} ~~~~~ \mathrm{(A)} \end{aligned}$$となります。
以下では$2$通りの方法で証明をします。
方法2が正式なものになりますが、直感的にはややわかりにくいかも知れません。
順序統計量に慣れていない方は直感的にわかりやすい方法1にまず取り組んでみてください。
(証明)
(方法1. 直感的に直接的に求める方法)
以下、$X_{(k)}$が$x \sim (x+dx)$に落ちる確率を$2$通りで求める。
まず、$X_{(k)}$が$x \sim (x+dx)$に落ちる確率は、$X_{(k)}$の確率密度関数$f_{(k)}(x)$を用いると、
$$\begin{aligned} f_{(k)} (x) dx \end{aligned}$$と書ける。
($f_{(k)}(x)$はあくまで確率密度だが、微小距離$dx$をかけることで確率となる)
一方で、$X_{(k)}$が$x \sim (x+dx)$に落ちる状況は下記なる状況となるので、
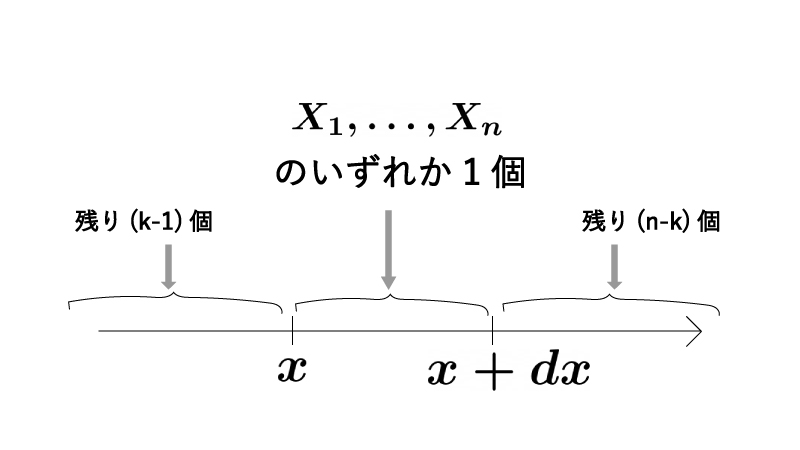
$X_{(k)}$が$x \sim (x+dx)$に落ちる確率は、
$$\begin{aligned} \underbrace{\binom{n}{1}}_{x \sim x+dxに落ちる1個の選び方} \cdot \underbrace{\binom{n-1}{k-1}}_{残り(k-1)個の選び方} \times \underbrace{f(x)dx}_{選ばれた1個がx \sim x+dxに落ちる確率} \cdot \underbrace{\{ F(x) \}^{k-1}}_{残り(k-1)個がx以下に落ちる確率} \cdot \underbrace{\{ 1-F(x) \}^{n-k}}_{残り(n-k)個がx(+dx)以上に落ちる確率} \end{aligned}$$となる。
以上から、
$$\begin{aligned} f_{(k)} (x) dx &= \binom{n}{1} \cdot \binom{n-1}{k-1} \times f(x)dx \cdot \{ F(x) \}^{k-1} \cdot \{ 1-F(x) \}^{n-k} \\[10px] \Rightarrow f_{(k)} (x) &= \binom{n}{1} \cdot \binom{n-1}{k-1} \times f(x) \cdot \{ F(x) \}^{k-1} \cdot \{ 1-F(x) \}^{n-k} \\[10px] \Rightarrow f_{(k)} (x) &= \frac{n!}{(k-1)! (n-k)!} \cdot f(x) \cdot \{ F(x) \}^{k-1} \cdot \{ 1-F(x) \}^{n-k} \end{aligned}$$
実際に上記Figを自分で書いてみるとよりイメージしやすくなると思います。
(証明)
(方法2. 分布関数を経て求める方法)
$X_{(k)}$の分布関数を$F_{(k)}(x)$とすると、
$$\begin{aligned} F_{(k)}(x) &= Pr\{ X_{(k)} \leqq x \} \\[10px] &= \sum_{r=k}^n Pr\{ X_{(k)} \leqq x {\small 、かつ、}x{\small より小さい}X_i{\small が}r{\small 個} \} \\[10px] &= \sum_{r=k}^n \left\{ \sum_{s \in \{ 1,\ldots, n \}, かつ, sの要素数がr個} \left( \prod_{i \in s} Pr\{ X_{i} \leqq x \} \cdot \prod_{i \notin s} Pr\{ X_{i} \gt x \} \right) \right\} \\[10px] &= \sum_{r=k}^n \left\{ \binom{n}{r} \cdot \{ F(x) \}^{r} \cdot \{ 1-F(x) \}^{n-r} \right\} \\[10px] &= \sum_{r=k}^n \frac{n!}{(n-r)!r!} \cdot \{ F(x) \}^{r} \cdot \{ 1-F(x) \}^{n-r} \end{aligned}$$となる。
この両辺を$x$で微分すると、
$$\begin{aligned} (\frac{d}{dx} F_{(k)}(x) =) f_{(k)}(x) &= \sum_{r=k}^n \left\{ \frac{n! (r f(x))}{(n-r)!r!} \cdot \{ F(x) \}^{r-1} \cdot \{ 1-F(x) \}^{n-r}-\underbrace{\frac{n!(n-r)f(x)}{(n-r)!r!} \cdot \{ F(x) \}^{r} \cdot \{ 1-F(x) \}^{n-r-1}}_{r=nで0になる} \right\} \\[10px] &= \sum_{r=k}^n \left\{ nf(x) \cdot \underbrace{\frac{(n-1)!}{(n-r)!(r-1)!} \cdot \{ F(x) \}^{r-1} \cdot \{ 1-F(x) \}^{n-r}}_{\Bin(n-1, F(x))の確率関数の形} \right\} \\[10px] &- \sum_{r=k}^{n-1} \left\{ nf(x) \cdot \underbrace{\frac{(n-1)!}{(n-r-1)!(r-1)!} \cdot \{ F(x) \}^{r} \cdot \{ 1-F(x) \}^{n-r-1}}_{\Bin(n-1, F(x))の確率関数の形} \right\} \\[10px] &= \sum_{m=k-1}^{n-1} \left\{ nf(x) \cdot \underbrace{\frac{(n-1)!}{(n-m-1)!m!} \cdot \{ F(x) \}^m \cdot \{ 1-F(x) \}^{n-m-1}}_{\Bin(n-1, F(x))の確率関数の形} \right\} \\[10px] &- \sum_{r=k}^{n-1} \left\{ nf(x) \cdot \underbrace{\frac{(n-1)!}{(n-r-1)!(r-1)!} \cdot \{ F(x) \}^{r} \cdot \{ 1-F(x) \}^{n-r-1}}_{\Bin(n-1, F(x))の確率関数の形} \right\} \\ &{\scriptsize (m=r-1とおいた)} \\[10px] &= nf(x) \cdot \frac{(n-1)!}{(n-k)!(k-1)!} \cdot \{ F(x) \}^{k-1} \cdot \{ 1-F(x) \}^{n-k} \\ &{\scriptsize (残るのはm=k-1の部分のみ)} \\[10px] &= \frac{n!}{(k-1)! (n-k)!} \cdot f(x) \cdot \{ F(x) \}^{k-1} \cdot \{ 1-F(x) \}^{n-k} \end{aligned}$$
それでは例題にチャレンジしてみましょう!
例題1.
$X_i \overset{i.i.d}\sim \U[0, \theta] ~ {\small (i=1, \ldots, n)}$である時、最大値$X_{(n)}$の確率密度関数$f_{(n)}(x) ~ {\small (0 \leqq x \leqq \theta)}$を求めよ。
ただし、$\mathrm{(A)}$は公式的に用いてはならない。
解答.(方法1. 直感的に直接的に求める方法)
$\U[0, \theta]$の確率密度関数、分布関数をそれぞれ$f(x), F(x)$とする。
まず、$X_{(n)}$が$x \sim (x+dx)$に落ちる確率は、$X_{(n)}$の確率密度関数$f_{(n)}(x)$を用いると、
$$\begin{aligned} f_{(n)} (x) dx \end{aligned}$$と書ける。
一方で、$X_{(n)}$が$x \sim (x+dx)$に落ちる状況は下記なる状況となるので、
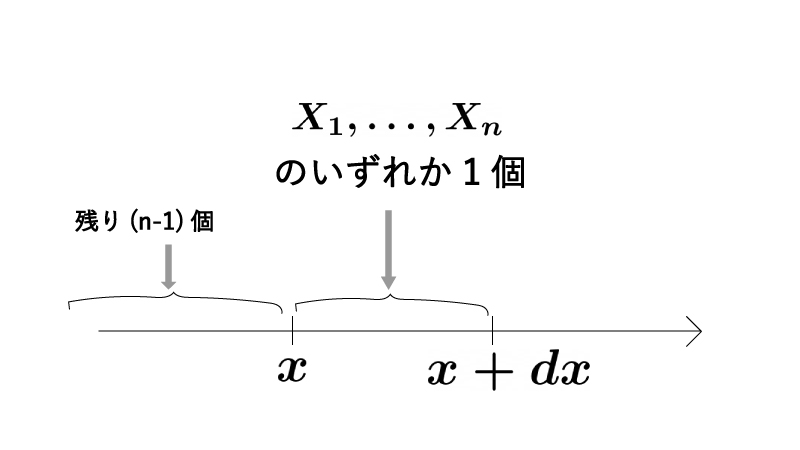
$X_{(n)}$が$x \sim (x+dx)$に落ちる確率は、
$$\begin{aligned} \underbrace{\binom{n}{1}}_{x \sim x+dxに落ちる1個の選び方} \times \underbrace{f(x)dx}_{選ばれた1個がx \sim x+dxに落ちる確率} \cdot \underbrace{\{ F(x) \}^{n-1}}_{残り(n-1)個がx以下に落ちる確率} \end{aligned}$$となる。
以上から、
$$\begin{aligned} f_{(n)} (x) dx &= \binom{n}{1} \times f(x)dx \cdot \{ F(x) \}^{n-1} \\[10px] &= n \times \frac{1}{\theta}dx \cdot (\frac{x}{\theta})^{n-1} \\[10px] \Rightarrow f_{(n)} (x) &= \frac{n}{\theta^n} x^{n-1} ~ {\small (i=1, \ldots, n)} \end{aligned}$$
解答.(方法2. 分布関数を経て求める方法)
$X_{(k)}$の分布関数を$F_{(k)}(x)$とすると、
$$\begin{aligned} F_{(k)}(x) &= Pr\{ X_{(k)} \leqq x \} \\[10px] &= Pr\{ X_1 \leqq x, \cdots, X_n \leqq x \} \\[10px] &= (\frac{x}{\theta})^n \end{aligned}$$となる。
この両辺を$x$で微分すると、
$$\begin{aligned} (\frac{d}{dx} F_{(k)}(x) =) f_{(k)}(x) = \frac{n}{\theta^n} x^{n-1} ~ {\small (i=1, \ldots, n)} \end{aligned}$$
それではもう$1$問!
例題2.
$X_i \overset{i.i.d}\sim \U[0, \theta] ~ {\small (i=1, \ldots, n)}$である時、下から$k$番目の値$X_{(k)}$の確率密度関数$f_{(k)} (x) ~ {\small (0 \leqq x \leqq \theta)}$を求めよ。
ただし、$\mathrm{(A)}$は公式的に用いてはならない。
解答.(方法1. 直感的に直接的に求める方法)
$\U[0, \theta]$の確率密度関数、分布関数をそれぞれ$f(x), F(x)$とする。
まず、$X_{(k)}$が$x \sim (x+dx)$に落ちる確率は、$X_{(k)}$の確率密度関数$f_{(k)}(x)$を用いると、
$$\begin{aligned} f_{(k)} (x) dx \end{aligned}$$と書ける。
一方で、$X_{(k)}$が$x \sim (x+dx)$に落ちる状況は下記なる状況となるので、

$X_{(k)}$が$x \sim (x+dx)$に落ちる確率は、
$$\begin{aligned} \underbrace{\binom{n}{1}}_{x \sim x+dxに落ちる1個の選び方} \cdot \underbrace{\binom{n-1}{k-1}}_{残り(k-1)個の選び方} \times \underbrace{f_i(x)dx}_{選ばれた1個がx \sim x+dxに落ちる確率} \cdot \underbrace{\{ F(x) \}^{k-1}}_{残り(k-1)個がx以下に落ちる確率} \cdot \underbrace{\{1-F(x)\}^{n-k}}_{残り(n-k)個がx(+dx)以上に落ちる確率} \end{aligned}$$となる。
以上から、
$$\begin{aligned} f_{(k)} (x) dx &= \binom{n}{1} \cdot \binom{n-1}{k-1} \times f_i(x)dx \cdot \{ F(x) \}^{k-1} \cdot \{1-F(x)\}^{n-k} \\[10px] &= \frac{n!}{(k-1)!(n-k)!} \cdot (\frac{1}{\theta})dx \cdot (\frac{x}{\theta})^{k-1} \cdot (1-\frac{x}{\theta})^{n-k} \\[10px] \Rightarrow f_{(k)} (x) &= \frac{n!}{(k-1)!(n-k)!} \cdot (\frac{1}{\theta}) \cdot (\frac{x}{\theta})^{k-1} \cdot (1-\frac{x}{\theta})^{n-k} \end{aligned}$$
解答.(方法2. 分布関数を経て求める方法)
$X_{(k)}$の分布関数を$F_{(k)}(x)$とすると、
$$\begin{aligned} F_{(k)}(x) &= Pr\{ X_{(k)} \leqq x \} \\[10px] &= \sum_{r=k}^n Pr\{ X_{(k)} \leqq x {\small 、かつ、}x{\small より小さい}X_i{\small が}r{\small 個} \} \\[10px] &= \sum_{r=k}^n \left\{ \sum_{s \in \{ 1,\ldots, n \}, かつ, sの要素数がr個} \left( \prod_{i \in s} Pr\{ X_{i} \leqq x \} \cdot \prod_{i \notin s} Pr\{ X_{i} \gt x \} \right) \right\} \\[10px] &= \sum_{r=k}^n \binom{n}{r} \cdot \{ F(x) \}^{r} \cdot \{ 1-F(x) \}^{n-r} \\[10px] &= \sum_{r=k}^n \frac{n!}{(n-r)!r!} \cdot \{ F(x) \}^{r} \cdot \{ 1-F(x) \}^{n-r} \end{aligned}$$となる。
この両辺を$x$で微分すると、
$$\begin{aligned} (\frac{d}{dx} F_{(k)}(x) =) f_{(k)}(x) &= \sum_{r=k}^n \left\{ \frac{n! (r f(x))}{(n-r)!r!} \cdot \{ F(x) \}^{r-1} \cdot \{ 1-F(x) \}^{n-r}-\underbrace{\frac{n!(n-r)f(x)}{(n-r)!r!} \cdot \{ F(x) \}^{r} \cdot \{ 1-F(x) \}^{n-r-1}}_{r=nで0になる} \right\} \\[10px] &= \sum_{r=k}^n \left\{ nf(x) \cdot \underbrace{\frac{(n-1)!}{(n-r)!(r-1)!} \cdot \{ F(x) \}^{r-1} \cdot \{ 1-F(x) \}^{n-r}}_{\Bin(n-1, F(x))の確率関数の形} \right\} \\[10px] -& \sum_{r=k}^{n-1} \left\{ nf(x) \cdot \underbrace{\frac{(n-1)!}{(n-r-1)!(r-1)!} \cdot \{ F(x) \}^{r} \cdot \{ 1-F(x) \}^{n-r-1}}_{\Bin(n-1, F(x))の確率関数の形} \right\} \\[10px] &= \sum_{m=k-1}^{n-1} \left\{ nf(x) \cdot \underbrace{\frac{(n-1)!}{(n-m-1)!m!} \cdot \{ F(x) \}^m \cdot \{ 1-F(x) \}^{n-m-1}}_{\Bin(n-1, F(x))の確率関数の形} \right\} \\[10px] -& \sum_{r=k}^{n-1} \left\{ nf(x) \cdot \underbrace{\frac{(n-1)!}{(n-r-1)!(r-1)!} \cdot \{ F(x) \}^{r} \cdot \{ 1-F(x) \}^{n-r-1}}_{\Bin(n-1, F(x))の確率関数の形} \right\} \\ &{\scriptsize (m=r-1とおいた)} \\[10px] &= nf(x) \cdot \frac{(n-1)!}{(n-k)!(k-1)!} \cdot \{ F(x) \}^{k-1} \cdot \{ 1-F(x) \}^{n-k} \\ &{\scriptsize (残るのはm=k-1の部分のみ)} \\[10px] &= \frac{n!}{(k-1)! (n-k)!} \cdot f(x) \cdot \{ F(x) \}^{k-1} \cdot \{ 1-F(x) \}^{n-k} \\[10px] &= \frac{n!}{(k-1)! (n-k)!} \cdot (\frac{1}{\theta}) \cdot ( \frac{x}{\theta} )^{k-1} \cdot ( 1-\frac{x}{\theta} )^{n-k} \end{aligned}$$
まとめ.
- 順序統計量の定義の確認と、その確率密度関数の導出を行った。






