$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}}$
「推測」とは、興味のある未知の母集団について、観測データからその特徴を推し測ることです。その中の$2$種類「推定」「検定」のうち、ここでは「検定」を扱います。
いきなりですが、『検定とは何か?』という問いに一言で答えられますか?
検定はやったことはありますが、『検定とは何か?』と改めて問われると難しいですね。
「推定」と対比してみるとわかりやすいかと思います。
「推定」とは真のパラメータをあてにいくことでしたが、「検定」とは真のパラメータが存在しうる空間を$2$つに分けてどちらに属するかを判定することです。
なるほどです!
1. 検定とは?
分布パラメータ$\theta$について、$\theta$のとりうる集合を$\Theta$として、
$$\begin{aligned} \Theta_0 \cup \Theta_1 &= \Theta \\ \Theta_0 \cap \Theta_1 &= \phi \end{aligned}$$と$\Theta$を$\Theta_0, \Theta_1$という$2$つの集合にわけて、 帰無仮説$H_0$、対立仮説$H_1$を
$$\begin{aligned} \begin{cases} H_0: \theta &\in \Theta_0 \\ H_1: \theta &\in \Theta_1 \end{cases} \end{aligned}$$と定める時、観測データから$H_0, H_1$のどちらを選択すべきかを判定します。
この判定のための関数を「検定関数(テスト関数)」といい、
$$\begin{aligned} \phi(\vec X) = \begin{cases} 0 ~~ ({\small H_0を選択}) \\ 1 ~~ ({\small H_1を選択}) \end{cases} \end{aligned}$$と入力データ(観測データ)に応じて$0$または$1$を返します。
「推定」では観測データ$\vec X$から真のパラメータをあてにいくための推定量$\hat{\theta}(\vec X)$を構成しましたが、「検定」では観測データ$\vec X$からどちらの仮説が正しいのかを判定するための検定関数$\phi (\vec X)$を構成したわけです。
慣例的には$\phi(\vec X)$が$0$または$1$のいずれを返すかは、検定統計量$T(\vec X)$と受容域・棄却域*との関係をもって記述されます。
具体的には、
- $T(\vec X)$が受容域$A$におちる:$T(\vec X) \in A \Rightarrow \phi(\vec X) = 0 ~~ ({\small H_0を選択})$
- $T(\vec X)$が棄却域$R$におちる:$T(\vec X) \in R \Rightarrow \phi(\vec X) = 1 ~~ ({\small H_1を選択})$
(ただし$A$と$R$は排反)
という判定がなされます。
(*:正確には「受容域」「棄却域」という用語は$\vec X$自体について定められるものの様ですが、慣例的には$T(\vec X)$に対して使用されているので、ここではその様に使用しています)
観測データから構成される$T(\vec X)$と、受容域$A$/棄却域$R$とが検定を特徴づけるのですね。
2. 検定の望ましさとは?
先述の流れにより検定はなされますが、そこには一定の確率でミスが生じます。
具体的には、
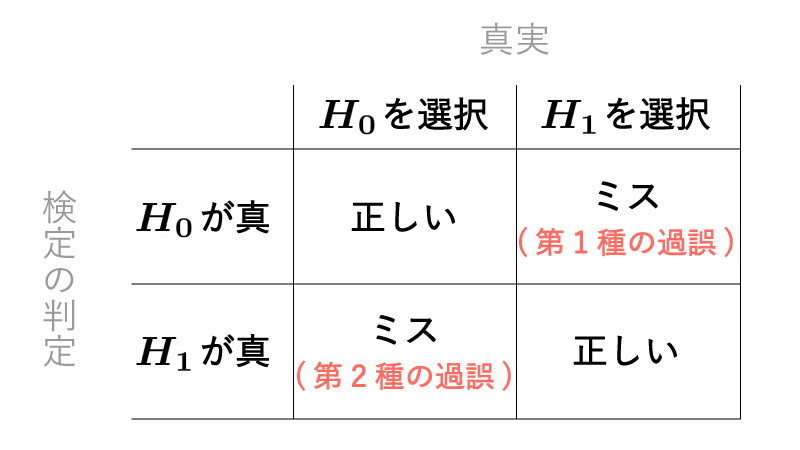
- $H_0$が真であるにも関わらず$H_1$を選択してしまう(「第$1$種の過誤」)
- $H_1$が真であるにも関わらず$H_0$を選択してしまう(「第$2$種の過誤」)
というミスが生じます。(Fig1)
Fig1.
第$1$種の過誤と第$2$種の過誤はトレードオフの関係にあり、どちらの発生確率をも$0$にすることはできません。
そこで歴史的に、 『第$1$種の過誤の発生確率を一定確率($\alpha$)以下に抑えた上で、第$2$種の過誤の発生確率を可能な限り下げる』 という手続きがとられてきました。
(第$2$種の過誤の発生確率はある程度大きくなりがちであり、そのため$H_0$が選択された場合には『暫定的にそれを受け入れる』という姿勢が求められます)
ここで事前に定めた”$\alpha$”を「(検定の)有意水準」と言います。
また$\theta (\in H_1)$に対して$H_1$が正しいと判定される確率$Pr_{\theta} \{ T(\vec X) \in R \} = E_{\theta} [\phi (\vec X)]$を「検出力」と言います。(検出力を高めることは第$2$種の過誤の発生確率を下げることと同義です)
上式は、$$\begin{aligned} E_{\theta} [\phi (\vec X)] &= 0 \times Pr_{\theta} \{ \phi(\vec X) = 0 \} + 1 \times Pr_{\theta} \{ \phi(\vec X) = 1 \} \\ &= Pr_{\theta} \{ \phi(\vec X) = 1 \} \\ &= Pr_{\theta} \{ T(\vec X) \in R \} \end{aligned}$$に由来しています。
ここまでをまとめると有意水準$\alpha$を定めた上で検出力を可能な限り高めたいわけですが、
対立仮説が単純仮説*$^1$である時に、有意水準$\alpha$の下で最も検出力が高い検定を「最強力検定」と言います。
対立仮説が複合仮説*$^2$の場合にはパラメータは$1$つに定まりませんが、いずれのパラメータについても最も検出力が高い検定を「一様最強力検定」と言います。
(補足)
*$^1$:$\theta = 0$、の様に分布パラメータがある一点に一致するという仮説
*$^2$:単純仮説ではない仮説。具体的には、$\theta \neq 0$、の様に分布パラメータがある集合に含まれるという仮説
例1.
$H_0$が単純仮説、$H_1$が複合仮説である様な検定$1$として、
$$\begin{aligned} &\begin{cases} H_0: \mu &= \mu_0 \\ H_1: \mu &\neq \mu_0 \end{cases} \end{aligned}$$なる検定を扱う。
この時にまず検定$2$として、$\mu_1 (\neq \mu_0)$に対して、
$$\begin{aligned} &\begin{cases} H_0: \mu &= \mu_0 \\ G_1: \mu &= \mu_1 \end{cases} \end{aligned}$$なる検定を扱う。
検定$2$の検定方式として、
- $T(\vec X)$が受容域$A$におちる:$T(\vec X) \in A \Rightarrow \phi(\vec X) = 0 ~~ ({\small H_0を選択})$
- $T(\vec X)$が棄却域$R$におちる:$T(\vec X) \in R \Rightarrow \phi(\vec X) = 1 ~~ ({\small {\color{red}{G_1}}を選択})$
(ただし$A$と$R$は排反)
というものは最強力検定であるとする。
この時、特に$A$や$R$に$\mu_1$を含まない場合には、検定$1$の検定方式として、
- $T(\vec X)$が受容域$A$におちる:$T(\vec X) \in A \Rightarrow \phi(\vec X) = 0 ~~ ({\small H_0を選択})$
- $T(\vec X)$が棄却域$R$におちる:$T(\vec X) \in R \Rightarrow \phi(\vec X) = 1 ~~ ({\small {\color{red}{H_1}}を選択})$
(ただし$A$と$R$は排反)
というものは一様最強力検定となる。
ここまで「1. 検定とは?」「2. 検定の望ましさとは?」においてストーリー仕立てで進めてきましたが、ストーリーを意識して説明できる様にしてください。
また、推定の望ましさは『推定量と真のパラメータの差分の$2$乗(平均$2$乗誤差)』で評価しましたが(参照:<不偏推定量>)、検定の望ましさは『有意水準を一定に定めた上での検出力の高さ』で評価することを抑えておいてください。
3. ネイマン・ピアソンの補題(定理)
(定理)
帰無仮説$H_0$と対立仮説$H_1$をともに単純仮説として($H_0: \theta=\theta_0, H_1: \theta=\theta_1$)、$H_0, H_1$の下での確率密度関数を$f(\vec x; \theta_0), f(\vec x; \theta_1)$とします。
この時、有意水準が$\alpha ~{\small (0 \leqq \alpha \leqq 1)}$である検定において、
- $\dfrac{f(\vec x; \theta_1)}{f(\vec x; \theta_0)} \leqq c \Rightarrow \phi(\vec X) = 0 ~~ ({\small H_0を選択})$
- $\dfrac{f(\vec x; \theta_1)}{f(\vec x; \theta_0)} \gt c \Rightarrow \phi(\vec X) = 1 ~~ ({\small H_1を選択})$
(ただし、$c$は$E_{\theta_0}[\phi(\vec X)] = \alpha$から求められる)
という検定が最強力検定になります。
- ネイマン・ピアソンの補題(定理)は、帰無仮説$H_0$と対立仮説$H_1$とがともに単純仮説である時に最強力検定の存在を保証するものです。注意点としては、その仮定が成立しない時(通常は$H_1$が複合仮説である時)の一様最強力検定の存在を保証するものではありません。
- 紹介したネイマン・ピアソンの補題(定理)は連続分布を想定したものであり、離散分布の場合には「確率化」という作業が追加されます。しかし本質的には同様であり、ここでは扱いません。
(証明)
$E_{\theta_0}[\phi(\vec X)] \textcolor{red}{\leqq} \alpha$なる任意の検定関数$\phi(\vec X)$と、
$$\begin{aligned} E_{\theta_0}[\phi_c(\vec X)] &= \alpha \\ \phi_c(\vec X) &= \begin{cases} 0 ~~ (if ~~ \dfrac{f(\vec x; \theta_1)}{f(\vec x; \theta_0)} \leqq c) \\ 1 ~~ (if ~~ \dfrac{f(\vec x; \theta_1)}{f(\vec x; \theta_0)} \gt c) \end{cases} \end{aligned}$$なる検定関数$\phi_c(\vec X)$について、
$$\begin{aligned} E_{\theta_1}[\phi_c(\vec X)] \geqq E_{\theta_1}[\phi(\vec X)] \end{aligned}$$を示せばよい。
(天下り的だが)まず、以下$\mathrm{(A)}$が成立することを示す。
$$\begin{aligned} E_{\theta_1}[\phi_c(\vec X)-\phi(\vec X)] \geqq c \cdot E_{\theta_0}[\phi_c(\vec X)-\phi(\vec X)] ~~~~~ \mathrm{(A)} \\ \iff \underbrace{\int (\phi_c(\vec x)-\phi(\vec x))}_{(1)} \cdot \{ \underbrace{f(\vec x;\theta_1)-cf(\vec x; \theta_0)}_{(2)} \} d\vec x \geqq 0 ~~~~~ \mathrm{(B)} \end{aligned}$$
$(2) \leqq 0$である時、上記定義から$\phi_c(\vec x) = 0$であり、$0 \leqq \phi(\vec x) \leqq 1$と合わせて$(1) \leqq 0$となるため、$\mathrm{(B)}$の$\int$内は非負となる。
$(2) \gt 0$である時、上記定義から$\phi_c(\vec x) = 1$であり、$0 \leqq \phi(\vec x) \leqq 1$と合わせて$(1) \geqq 0$となるため、$\mathrm{(B)}$の$\int$内は非負となる。
以上から$\mathrm{(B)}$の$\int$内は常に非負であるため$\mathrm{(B)}$は成立し、即ち$\mathrm{(A)}$も成立する。
よって、
$$\begin{aligned} E_{\theta_1}[\phi_c(\vec X)-\phi(\vec X)] &\geqq c \cdot E_{\theta_0}[\phi_c(\vec X)-\phi(\vec X)] \\ &{\scriptsize ((A)より)} \\[10px] &= c (E_{\theta_0}[\phi_c(\vec X)]-E_{\theta_0}[\phi(\vec X)]) \\[10px] &= c(\alpha-E_{\theta_0}[\phi(\vec X)]) \\ &{\scriptsize (定義よりE_{\theta_0}[\phi_c(\vec X)]=\alpha)} \\[10px] &\geqq 0 \\ &{\scriptsize (E_{\theta_0}[\phi(\vec X)] \textcolor{red}{\leqq} \alphaより)} \end{aligned}$$が成立するため、
$$\begin{aligned} E_{\theta_1}[\phi_c(\vec X)] \geqq E_{\theta_1}[\phi(\vec X)] \end{aligned}$$は示された。
例2.
$X_i \overset{i.i.d}\sim \N(\mu, \sigma^2) ~~ {\small (i=1, \ldots, n)}$である時、ある$\mu_0, \mu_1$に対して、帰無仮説$H_0$、対立仮説$H_1$を
$$\begin{aligned} \begin{cases} H_0: \mu = \mu_0 \\ H_1: \mu = \mu_1 \end{cases} \end{aligned}$$と定めた検定を行う。(つまり$H_0, H_1$ともに単純仮説)
まず$\dfrac{f(\vec x; \mu_1)}{f(\vec x; \mu_0)}$について、
$$\begin{aligned} \dfrac{f(\vec x; \mu_1)}{f(\vec x; \mu_0)} &= \dfrac {\dfrac{1}{(2 \pi \sigma^2)^{\frac{n}{2}}} \exp[-\dfrac{1}{2 \sigma^2} \sum_{i=1}^{n} (x_i-\mu_1)^2]} {\dfrac{1}{(2 \pi \sigma^2)^{\frac{n}{2}}} \exp[-\dfrac{1}{2 \sigma^2} \sum_{i=1}^{n} (x_i-\mu_0)^2]} \\[10px] &= \exp [-\dfrac{1}{2 \sigma^2} \{ \sum_{i=1}^{n} (x_i-\mu_1)^2-\sum_{i=1}^{n} (x_i-\mu_0)^2 \}] \\[10px] &= \exp [-\dfrac{1}{2 \sigma^2} \{ -2(\mu_1-\mu_0) \sum_{i=1}^{n} x_i + n(\mu_1^2-\mu_0^2) \}] \\[10px] &= \exp [-\dfrac{1}{2 \sigma^2} \{ -2n(\mu_1-\mu_0) \cdot \bar{x}_n + n(\mu_1^2-\mu_0^2) \}] \\[10px] &= \exp [\dfrac{n}{\sigma^2} (\mu_1-\mu_0) \cdot \bar{x}_n-\dfrac{n}{2 \sigma^2}(\mu_1^2-\mu_0^2)] ~~~~~ \mathrm{(C)} \end{aligned}$$と整理される。
すると、ネイマン・ピアソンの補題(定理)より最強力検定は以下に帰着される。
- $\dfrac{f(\vec x; \mu_1)}{f(\vec x; \mu_0)} \leqq c \Rightarrow \phi(\vec X) = 0 ~~ ({\small H_0を選択})$
- $\dfrac{f(\vec x; \mu_1)}{f(\vec x; \mu_0)} \gt c \Rightarrow \phi(\vec X) = 1 ~~ ({\small H_1を選択})$
(ただし、$c$は$E_{\theta_0}[\phi(\vec X)] = \alpha$から求められる)
これを$\mathrm{(C)}$を用いて簡潔な形にすると、
- $(\mu_1-\mu_0) \cdot \bar{x}_n \leqq c^{\prime} \Rightarrow \phi(\vec X) = 0 ~~ ({\small H_0を選択})$
- $(\mu_1-\mu_0) \cdot \bar{x}_n \gt c^{\prime} \Rightarrow \phi(\vec X) = 1 ~~ ({\small H_1を選択})$
(ただし、$c^{\prime}$は$\mathrm{(C)}$と$c$から一意に定まる)
となる。
- (先述の通り)ネイマン・ピアソンの補題(定理)は、帰無仮説$H_0$と対立仮説$H_1$とがともに単純仮説である時に最強力検定の存在を保証するものであり、その仮定が成立しない時(通常は$H_1$が複合仮説である時)の一様最強力検定の存在を保証するものではありません。
しかし、対立仮説の分布パラメータを任意の$1$点$\theta_1 (\in \Theta_1)$に固定して導出される最強力検定が$\theta_1$に依存しないのであれば、その最強力検定は一様最強力検定となります。一方で$\theta_1$に依存するのであれば、一様最強力検定は存在しません。
まとめ.
- 検定とは分布パラメータについての仮説(帰無仮説と対立仮説)のどちらを選択すべきかを、観測データから判定することである。
- 検定の望ましさとは、第$1$種の過誤の発生確率を一定以下に抑えた上で第$2$種の過誤の発生確率(または検出力)で測られる。第$2$種の過誤の発生確率が低い(または検出力が高い)検定の方が望ましい。
- 対立仮説が単純仮説である時に、最も望ましい検定を「最強力検定」と言う。
- ネイマン・ピアソンの補題(定理)は、最強力検定を与える。




