$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}} \\ \gdef \indep {\mathop{\perp\!\!\!\!\perp}} \\ \gdef \tr {\mathrm{tr}}$
今回は『因子分析』ですか。
名前しか聞いたことがないです。
全く問題ありません。
因子分析は、前回扱った『主成分分析』と同様に新しく変数を作り出すという点では共通しています。しかしながら、観測された変数の前(背景)にある変数を作り出すのか、後にある変数を作り出すのかが異なります。
その違いを押さえておくのが混乱を防ぐのに大事です。
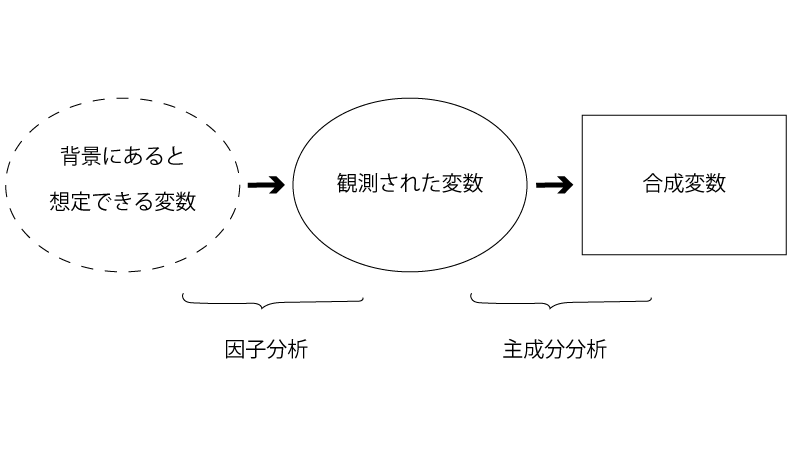
観測された変数に対して、その前(背景)にある変数を作り出すのが因子分析、その後にある変数を作り出すのが主成分分析ということですね。
その通りです。
1. 因子分析のモデリング
因子分析では観測変数の背景にある共通因子と、共通因子では説明しきることができない部分(独自因子)からモデリングされます。
即ち、$p$変数のデータがあるとして、
・$\vec x ~~ (\in \mathbb{R}^p)$:観測変数(のベクトル)
・$\vec f ~~ (\in \mathbb{R}^m)$:共通因子(のベクトル)
・$\vec e ~~ (\in \mathbb{R}^p)$:独自因子(のベクトル)
(ただし$p \gt m$)
・$\vec f \sim \N(\vec 0, \Phi)$
・$\vec e \sim \N(\vec 0, \Psi) ~~ (=diag(\psi_1, \cdots, \psi_p))$
・$\vec f$と$\vec e$は独立
・$\vec \mu ~~ (\in \mathbb{R}^p)$
・$\Lambda ~~ (\in \mathbb{R}^{p \times m})$
として、
$$\begin{aligned} \vec x = \vec \mu + \Lambda \vec f + \vec e \end{aligned}$$とモデリングします。
この時、
$$\begin{aligned} E[\vec x] &= E[\vec \mu + \Lambda \vec f + \vec e] \\[10px] &= \vec \mu \\ &{\scriptsize(E[\vec f] = E[\vec e] = \vec 0)} \\[50px] V[\vec x] &=: \Sigma \\[10px] &= V[\vec \mu + \Lambda \vec f + \vec e] \\[10px] &= \Lambda V[\vec f] \Lambda^{\top} + V[\vec e] \\ &{\scriptsize(V[\vec \mu] = \vec 0)} \\[10px] &= \Lambda \Phi \Lambda^{\top} + \Psi \end{aligned}$$となります。
上式のモデリングのイメージとしては、『$p$変数のデータ$=$平均$+m$変数のデータ(に行列$\Lambda$を噛ませて$p$変数に調整したもの)$+$独自因子(誤差)』となります。なお、このモデリングでは、$p$変数が背景にある$m$変数で説明できるとしてるので、『$m$因子モデル』といいます。また”$\Lambda$”は『因子負荷量(行列)』といいます。
様々な文字がでてきたたま一旦整理しましょう。
$\vec x$のみが観測される量で、その分布パラメータは$(\vec \mu, \Sigma, \Phi, \Psi, \Lambda)$の5つとなります。(確率変数自体は分布パラメータではありません)
$\Sigma$は$\Phi, \Psi, \Lambda$で表現されるため、分布パラメータは実質$(\vec \mu, \Phi, \Psi, \Lambda)$の4つとなります。
(補足)
$$\begin{aligned} \underbrace{\Sigma}_{\sigma_i} &= \underbrace{\Lambda \Phi \Lambda^{\top}}_{y_{i}} + \underbrace{\Psi}_{\psi_i} \\ &{\scriptsize(下に記載した文字はそれぞれの対角成分)} \end{aligned}$$は、全体のばらつき$\Sigma$を共通のばらつき$\Lambda \Phi \Lambda^{\top}$と独自のばらつき$\Psi$に分解する式と見ることができます。
この式の対角成分に着目すると、
$$\begin{aligned} \sigma_i^2 &= y_i^2 + \psi_i^2 \\ \Rightarrow \underbrace{\frac{y_i^2}{\sigma_i^2}}_{\bullet} + \underbrace{\frac{\phi_i^2}{\sigma_i^2}}_{\circ} &= 1 \end{aligned}$$となり、$\bullet$を『共通性』、$\circ$を『独自性』と言います。
2. 因子分析モデルにおける不定性
因子分析モデルの実質的なパラメータ$(\vec \mu, \Phi, \Psi, \Lambda)$は制約条件を課さない状態では一意に定まらず、これを『不定性』と言います。
主に不定性には2つ『(広義の)回転の不定性』『(狭義の)回転の不定性』があり、以下ではそれぞれ紹介します。
なぜ『回転の』とついてるのか疑問に持たれるかもしれませんが、一旦置いておいてください。読み進めていただき、『4.回転』までいけば理解することができます。
2-1. (広義の)回転の不定性
ある正則行列(逆行列をもつ行列)$A ~~ (\in \mathbb{R}^{m \times m})$を用いて、
$$\begin{aligned} \tilde{\vec f} &= A \vec f \\ \tilde{\Lambda} &= \Lambda A^{-1} \end{aligned}$$と変換した時、
( この時、$\tilde{\vec f} \sim \N(\vec 0, \tilde{\Phi})$とすると、
$$\begin{aligned} \tilde{\Phi} &= V[\tilde{\vec f}] \\ &= V[A \vec f] \\ &= A V[\vec f] A^{\top} \\ &= A \Phi A^{\top} \end{aligned}$$となります。)
$$\begin{aligned} \vec x &= \vec \mu + \tilde{\Lambda} \tilde{\vec f} + \vec e \\ &= \vec \mu + (\Lambda A^{-1})(A \vec f) + \vec e \\ &= \vec \mu + \Lambda \vec f + \vec e \end{aligned}$$と同じ因子分析モデルに従うことになります。
つまり、$(\vec \mu, \Psi)$をfixしたとしても$(\Phi, \Lambda)$は一意に定まりません。
そこで対策をとります。
スケーリングの自由度を減らすため、各共通因子の分散が$1$の場合、即ち、$\Phi$の対角成分を$1$とする場合を考えるのです。
この様に、各共通因子の分散が$1$となるモデルを『斜交モデル』と言います。
斜交モデルでは各共通因子それぞれの分散は$1$ですが、各共通因子の間の共分散は$0$とは限らないため、各共通因子間には一般に相関があります。
さらに、斜交モデルよりも強い制約条件として、$\Phi = I ~~\small{(単位行列)}$、としたモデルを『直交モデル』と言います。
直交モデルでは各共通因子それぞれの分散は$1$で、各共通因子の間の共分散は$0$とであるため、各共通因子間には相関がありません。
(広義の)回転の不定性からすべてのモデルは直交モデルに帰着することができるため、因子分析のパラメータの初期解を求めるにあたり、直交モデルを用いるのが基本となります。
2-2. (狭義の)回転の不定性
先述の通り、直交モデル、即ち、$\Phi = I ~~(単位行列)$、としたモデルを考えます。
ある直交行列*$Q ~~ (\in \mathbb{R}^{m \times m})$を用いて、
(*:転置行列と逆行列が等しくなる正方行列。即ち、$Q Q^{\top} = Q^{\top} Q = I$、を満たす。)
$$\begin{aligned} \tilde{\vec f} &= Q^{\top} \vec f \\ \tilde{\Lambda} &= \Lambda Q \end{aligned}$$と変換した時、
(この時、$\tilde{\vec f} \sim \N(\vec 0, \tilde{\Phi})$とすると、
$$\begin{aligned} \tilde{\Phi} &= V[\tilde{\vec f}] \\ &= V[Q^{\top} \vec f] \\ &= Q^{\top} V[\vec f] Q \\ &= Q^{\top} I Q \\ &{\scriptsize(V[\vec f] = \Phi = I)} \\ &= Q^{\top} Q \\ &= I (=\Phi) \end{aligned}$$となります。
つまり、変換後の$\tilde{\Phi}$の分散は$\Phi$の分散(単位行列$I$)と同じということです。)
$$\begin{aligned} \vec x &= \vec \mu + \tilde{\Lambda} \tilde{\vec f} + \vec e \\ &= \vec \mu + (\Lambda Q) (Q^{\top} \vec f) + \vec e \\ &= \vec \mu + \Lambda (Q Q^{\top}) \vec f + \vec e \\ &= \vec \mu + \Lambda \vec f + \vec e \end{aligned}$$と同じ因子分析モデルに従うことになります。
つまり、$(\vec \mu, \Phi, \Psi)$をfixしたとしても$\Lambda$は一意に定まりません。
そこで対策をとります。
(天下り的ではありますが)以下の$\Lambda$についての制約条件A&Bを追加することで、$\Lambda$は一意に定まることが知られており**、これを活用します。
・制約条件A:『$\Lambda^{\top} \Psi^{-1} \Lambda$の非対角成分が$0$(即ち、『$\Lambda^{\top} \Psi^{-1} \Lambda$が対角行列)』
・制約条件B:『$(\delta_{kl}:=) \Lambda^{\top} \Psi^{-1} \Lambda$に対して、$\delta_{11} \gt \delta_{22} \gt \cdots \gt \delta_{mm}$』
(**:ただし、$\Lambda$の列単位での正負の反転の自由度は残ります。)
制約条件Aについては完全に天下り的ですが、制約条件Bについては対角成分の並び方を1つに定めるためのものです。
3. 分布パラメータの推定
『2.因子分析モデルにおける不定性』の話をまとめると、観測データ$\vec x$からモデルの分布パラメータ$(\vec \mu, \Phi, \Psi, \Lambda)$を推定しようとしても、『2-1.(広義の)回転の不定性』『2-2.(狭義の)回転の不定性』のために、$(\vec \mu, \Phi, \Psi, \Lambda)$を一意に推定することができないということでした。
そこで、
・$\Phi = I$(直交モデル)
・$\Lambda^{\top} \Psi^{-1} \Lambda$の非対角成分が$0$(制約条件A)
・$(\delta_{kl}:=) \Lambda^{\top} \Psi^{-1} \Lambda$に対して、$\delta_{11} \gt \delta_{22} \gt \cdots \gt \delta_{mm}$(制約条件B)
という3つの制約条件を課した上で、最尤法による推定を行います。
なお、この様にして得られた解を『初期解』と言います。
具体的には以下の様な流れになります。
$$\begin{aligned} f(\vec x; \vec \mu, \Sigma) &= \frac{1}{(2 \pi)^{\frac{n}{2}} |\Sigma|^{\frac{1}{2}}} \exp \{ -\frac{1}{2} \textcolor{red}{ (\vec x-\vec \mu)^{\top} \Sigma^{-1} (\vec x-\vec \mu) } \} \\ &= \frac{1}{(2 \pi)^{\frac{n}{2}} |\Sigma|^{\frac{1}{2}}} \exp \{ -\frac{1}{2} \tr [\Sigma^{-1} (\vec x-\vec \mu) (\vec x-\vec \mu)^{\top}] \} \\ &{\scriptsize(上式の赤文字部分はスカラーなので\trをとることができ、その上で中味の順序を入れ替えた)} \\[10px] \Rightarrow l(\vec \mu, \Phi, \Psi, \Lambda) &= \log f(\vec x; \vec \mu, \Sigma) \\ &= -\frac{n}{2} \log(2 \pi)-\frac{1}{2} \log |\Sigma|-\frac{1}{2} \tr[\Sigma^{-1} (\vec x-\vec \mu) (\vec x-\vec \mu)^{\top}] \\ &= -\frac{n}{2} \log(2 \pi)-\frac{1}{2} \log | \Lambda \Phi \Lambda^{\top} + \Psi |-\frac{1}{2} \tr[ (\Lambda \Phi \Lambda^{\top} + \Psi)^{-1} (\vec x-\vec \mu) (\vec x-\vec \mu)^{\top} ] ~~~~~ \mathrm{(A’)} \\ &= -\frac{n}{2} \log(2 \pi)-\frac{1}{2} \log | \Lambda \Lambda^{\top} + \Psi |-\frac{1}{2} \tr[ (\Lambda \Lambda^{\top} + \Psi)^{-1} (\vec x-\vec \mu) (\vec x-\vec \mu)^{\top} ] ~~~~~ \mathrm{(A)} \\ &{\scriptsize(\Phi = I)} \end{aligned}$$
以下制約条件A/Bを加味した上で$\mathrm{(A)}$の最大化をしたいのですが、それをニュートン・ラプソン法で直接的に解くのは難しいです。(ちなみに、$\vec \mu$の最尤推定値は$\bar{\vec x}$となります)
しかしながら、うまく式変形をすることでそれを別方式で解くことができると知られています。
(詳しくはArak Mathai Mathai『Factor Analysis Revisited』2021.などを参照ください)
因子分析の計算を手計算ですることはごく稀で、基本的には統計解析ソフトにあるアルゴリズムを使うことになるはずなので、心配はありません。
4. 回転
『3.分布パラメータの推定』では直交モデルに制約条件A/Bを課すことで、一意な初期解$(\vec \mu_0, \Phi_0, \Psi_0, \Lambda_0)$が得られました。
(ただし、$\vec \mu_0 = \bar{\vec x}, \Phi_0 = I$)
因子分析では観測された変数の前(背景)にある変数に興味があるので、共通因子$\vec f_0$と因子負荷量$\Lambda_0$に注目することになります。
(ただし、初期解に対応する共通因子を$\vec f_0$と置いた)
その$\vec f_0, \Lambda_0$の解釈性が十分である時(解釈できる時)にはそのままで良いですが、解釈性が不十分である時(解釈しがたい時)には、解釈性を高めるために『回転』という作業を行います。
具体的には下記に紹介する『直交回転』ないし『斜交回転』を試すことになります。
これらはそれぞれ『2-2.(狭義の)回転の不定性』ないし『2-1.(広義の)回転の不定性』で示した内容を利用したものになっています。
4-1. 直交回転
$\vec f_0, \Lambda_0$に対して、ある直交行列$Q ~~ (\in \mathbb{R}^{m \times m})$を用いて、
$$\begin{aligned} \vec f_1 &= Q^{\top} \vec f_0 \\ \Lambda_1 &= \Lambda_0 Q \end{aligned}$$と変換することが『直交回転』と言います。
( この時、$\vec f_1 \sim \N(\vec 0, \Phi_1)$とすると、
$$\begin{aligned} \Phi_1 &= I \end{aligned}$$となりました。(『2-2.(狭義の)回転の不定性』参照)
これは、直交回転後の共通因子の分散共分散行列$\Phi_1$における各共通因子が無相関、つまりは、上記の通り軸の直交性が保たれる、ということです。 )
これは直交モデルの範囲内で共通因子と因子負荷量の解釈性を高める作業になります。
因子分析を初めて学ぶ方はイメージが湧かないと思うので、以下例を出してみます。
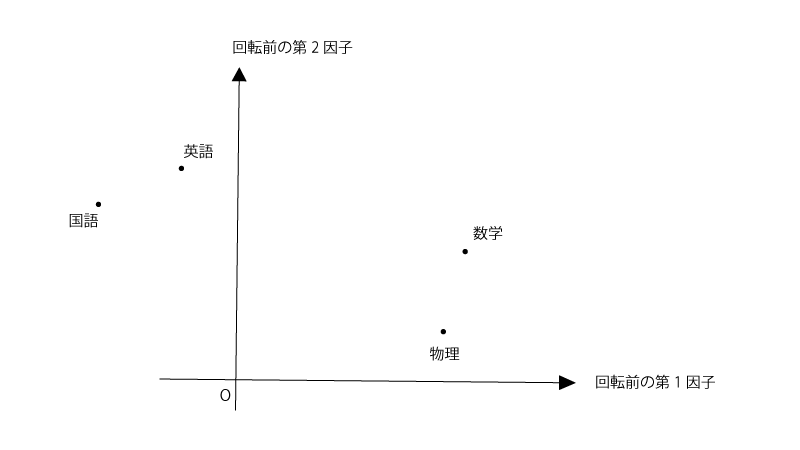
ここで、ある学生の集団を対象に数学、物理、英語、国語のテストの点数結果を収集したとします。
観測変数(数学、物理、英語、国語)と共通因子(ここでは2つとします)との関係を『3.分布パラメータの推定』にある通りにモデリングし、その関係をプロットすると以下の様になりました。
(直交モデルを使用してるため、第一因子と第二因子の軸は直交してます)
直交回転をするというのは下記の様に共通因子の軸を、軸の直交性は保ったままに、回転させることです。
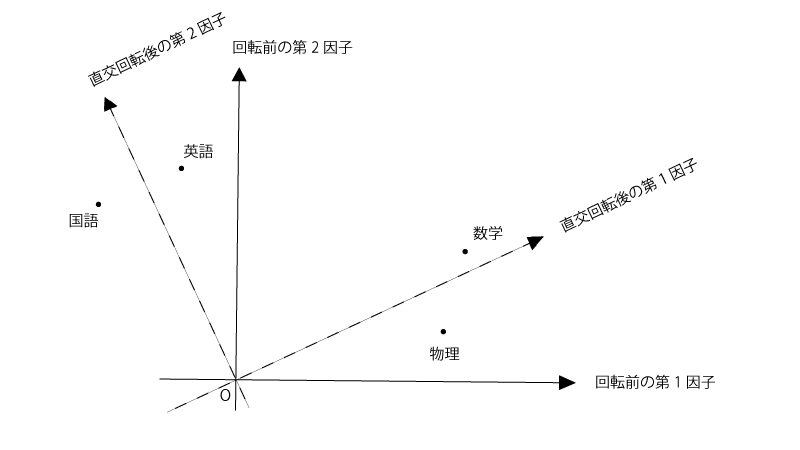
元々のプロットでも第一因子や第二因子の解釈はできなくもなさそうですが、直交回転させたあとの方が当てはまりがよい感じですね。直交回転させたあとの第一因子・第二因子はそれぞれ『理系科目の能力』『文系科目の能力』といった形で解釈できそうです。
その通りですね。なお、共通因子の解釈のしやすさの基準として『バリマックス基準』があり、それを最大化する方法を『バリマックス法』と言います。ここでは詳細は割愛します。
4-2. 斜交回転
$\vec f_0, \Lambda_0$に対して、ある正則行列$A ~~ (\in \mathbb{R}^{m \times m})$を用いて、
$$\begin{aligned} \vec f_2 &= A \vec f_0 \\ \Lambda_2 &= \Lambda_0 A^{-1} \end{aligned}$$と変換することが『斜交回転』と言います。
(この時、$\vec f_2 \sim \N(\vec 0, \Phi_2)$とすると、
$$\begin{aligned} \Phi_2 &= A \Phi_0 A^{\top} \\ &= A A^{\top} \\ &{\scriptsize(\Phi_0 = I)} \end{aligned}$$となりました。(『2-1.(広義の)回転の不定性』参照) )
これは斜交モデルの範囲内で共通因子と因子負荷量の解釈性を高める作業になります。
また例を見てみましょう。
(上記とは別の)ある学生の集団を対象に数学、物理、英語、国語のテストの点数結果を収集したとします。
観測変数(数学、物理、英語、国語)と共通因子(ここでは2つとします)との関係を『3.分布パラメータの推定』にある通りにモデリングし、その関係をプロットすると以下の様になりました。
(直交モデルを使用してるため、第一因子と第二因子の軸は直交してます)
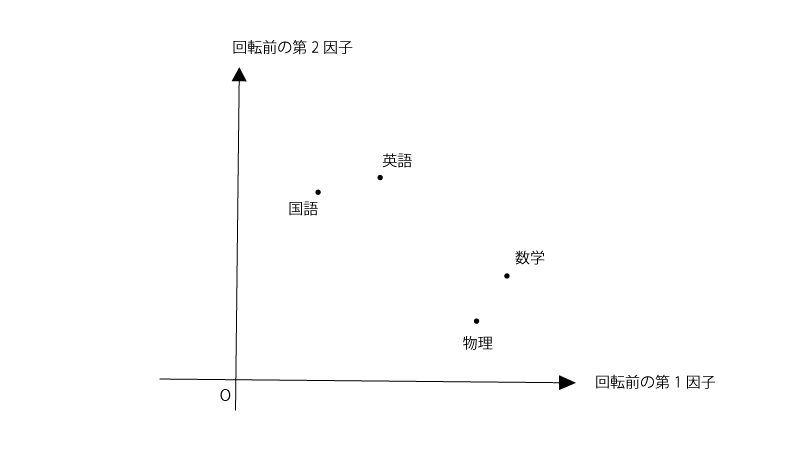
斜交回転をするというのは下記の様に共通因子の軸を、軸の直交性を保つ必要なく、回転させることです。
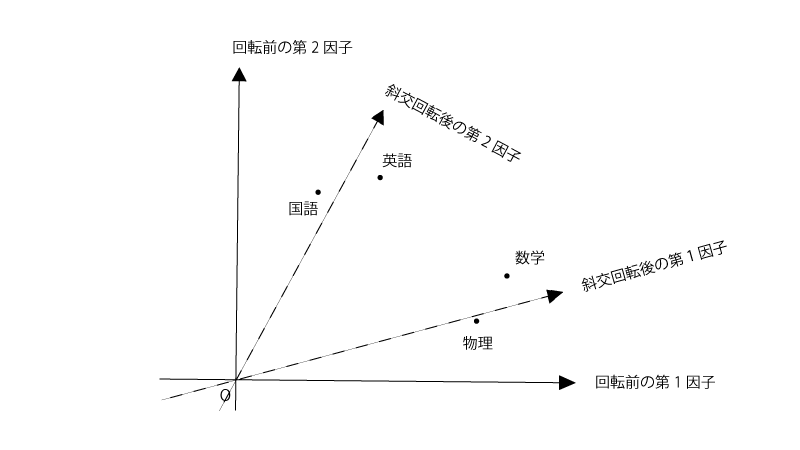
元々のプロットでも第一因子や第二因子の解釈はできなくもなさそうですが、斜交回転させたあとの方が当てはまりがよい感じですね。斜交回転させたあとの第一因子・第二因子はそれぞれ『理系科目の能力』『文系科目の能力』といった形で解釈できそうです。まあ上記と同じになりますが。
その通りですね。なお、共通因子の解釈のしやすさを最大化する方法として『プロマックス法』などがありますが、ここでは詳細は割愛します。一点注意としては、『4-1.直交回転』をさせた後の第一因子と第二因子は軸の直交性が保たれる、すなわち、独立でしたが、『4-2.斜交回転』をさせた後の第一因子と第二因子の軸は直交性が保たれるとは限らない、すなわち、独立とは必ずしもなりません。
つまりは、『4-1.直交回転』をさせた後の第一因子と第二因子は軸と、『4-2.斜交回転』をさせた後のそれらは、解釈の与え方が変わってくるかもしれないということですね。
その通りです。今回は同じ解釈を与えましたが、『4-1.直交回転』の場合には『理系科目の能力と文系科目の能力は独立』といった前提をおいており、『4-2.斜交回転』の場合には『理系科目の能力と文系科目の能力は部分的に相関』しているといった前提を置いてることになります。
(補足1)
今回は斜交回転として、ある正則行列$A ~~ (\in \mathbb{R}^{m \times m})$を$\vec f_0, \Lambda_0$に作用させました。
後出しにはなりますが、$A$が満たすべき制約条件が存在します。
それを確認しましょう。
斜交回転後の共通因子の分散共分散行列$\Phi_2$について、
$$\begin{aligned} \Phi_2 &= A \Phi_0 A^{\top} \\ &= A A^{\top} \\ &{\scriptsize(\Phi_0 = I)} \end{aligned}$$となりますが、斜交モデルの必要条件から、$\Phi_2$の各対角成分はすべて$1$である必要があります。
すなわち、$A$が満たすべき制約条件とは『$A A^{\top}$の各対角成分が$1$』となります。
ちなみにですが、直交回転させた場合も斜交回転させた場合も、その前後で尤度は変化しません。
この説明については本記事のボリュームが増えてしまったため、興味がある方のみ<補足.因子分析_回転前後の尤度>を参照してください。
(補足2)
因子分析には実は2種類:『検証的因子分析』『探索的因子分析』があります。
前者はデータ解析をする前に『背景にあると想定できる変数』を想定しておき、データ解析をしてみてその想定が妥当かを検証するというものです。
後者はデータ解析をする前には『背景にあると想定できる変数』を想定せず、データ解析をしてみて、データから『背景にあると想定できる変数』の想定(解釈)を与えるというものです。
本記事では『探索的因子分析』を意図しています。
これまで長く因子分析の理論を扱ってきましたが、以下では例題を通じて因子分析のイメージを確立してください。
例題1.
100人が5教科(英語、数学、理科、社会、国語)のテストを受けた。
各教科について標準化を行った上で、直交モデル・2因子モデルで解析をしたところ、(各因子に対する)因子負荷量の初期解は下記の通り得られた。
| 第1因子 | 第2因子 | |
| 英語 | 0.1 | 0.9 |
| 数学 | 0.8 | 0.1 |
| 理科 | 0.9 | 0.1 |
| 社会 | 0.2 | 0.8 |
| 国語 | 0.1 | 0.9 |
この時、以下の問いに答えよ。
(1). 第1因子、第2因子はそれぞれどの様に解釈できるか。
(2). 数学の共通性と独自性を求めよ。
(3). Aさん、Bさん、Cさんの(英語、数学、理科、社会、国語)の点数はそれぞれ$(60, 90, 85, 55, 60), (60, 50, 55, 85, 90), (70, 70, 70, 70, 70)$であった。
Aさん、Bさん、Cさんの因子スコアの候補が$(0.5, -0.5), (1.2, -1.5), (-1.0, 1.0)$である時、Aさんの因子スコアはどれであるか。
解答.
この例題と『1. 因子分析のモデリング』における『$\vec x = \vec \mu + \Lambda \vec f + \vec e$』の対応をまず確認しておく。
$i~~\small{(i=1,\cdots, 100)}$番目の人の点数ベクトル$\vec x_i$を、
$$\begin{aligned} \vec x_i = \begin{pmatrix} x_{i,1} (英語) \\ x_{i,2} (数学) \\ x_{i,3} (理科) \\ x_{i,4} (社会) \\ x_{i,5} (国語) \end{pmatrix} \end{aligned}$$とする。
$\vec x_i, \vec x_j ~~ \small{(i \neq j)}$を考えると、
$$\begin{aligned} \vec x_i &= \begin{pmatrix} x_{i,1} \\ x_{i,2} \\ x_{i,3} \\ x_{i,4} \\ x_{i,5} \end{pmatrix} = \underbrace{\vec \mu}_{=\vec 0 ~~ (標準化されてる)} + \underbrace{\begin{pmatrix} 0.1 & 0.9 \\ 0.8 & 0.1 \\ 0.9 & 0.1 \\ 0.2 & 0.8 \\ 0.1 & 0.9 \end{pmatrix}}_{\Lambda} \underbrace{\begin{pmatrix} f_{i,1} \\ f_{i,2} \end{pmatrix}}_{\vec f_i} + \underbrace{\begin{pmatrix} e_{i,1} \\ e_{i,2} \\ e_{i,3} \\ e_{i,4} \\ e_{i,5} \end{pmatrix}}_{\vec e_i} \\ \vec x_j &= \begin{pmatrix} x_{j,1} \\ x_{j,2} \\ x_{j,3} \\ x_{j,4} \\ x_{j,5} \end{pmatrix} = \underbrace{\vec \mu}_{=\vec 0 ~~ (標準化されてる)} + \underbrace{\begin{pmatrix} 0.1 & 0.9 \\ 0.8 & 0.1 \\ 0.9 & 0.1 \\ 0.2 & 0.8 \\ 0.1 & 0.9 \end{pmatrix}}_{\Lambda} \underbrace{\begin{pmatrix} f_{j,1} \\ f_{j,2} \end{pmatrix}}_{\vec f_j} + \underbrace{\begin{pmatrix} e_{j,1} \\ e_{j,2} \\ e_{j,3} \\ e_{j,4} \\ e_{j,5} \end{pmatrix}}_{\vec e_j} \\ \end{aligned}$$の様にモデリングされている。
($\vec \mu, \Lambda$は共通であり、$\vec f, \vec e$が対象によって異なる)
(1).
第1因子に対する因子負荷量は理系科目(数学、理科)で大きく、文系科目(英語、社会、国語)で小さい。よって、第1因子は『理系の能力の高さ』と解釈される。
一方で第2因子に対する因子負荷量は理系科目で小さく、文系科目で大きい。よって、第2因子は『文系能力の高さ』と解釈される。
(注意:今回は直交モデルを扱ってるため、『理系の能力の高さ』『文系の能力の高さ』は独立しているという仮定をしている)
(2).
数学の共通性は、$0.8^2 + 0.1^2 = 0.65$、である。
数学の独自性は、$1-0.65 = 0.35$、である。
(補足).
$i$番目の人の数学の点数$x_{i,2}(=0.8 f_{i,1} + 0.1 f_{i,2} + e_{i,2})$についての分散をとると、
$$\begin{aligned} V[x_{i,2}] &= V[0.8 f_{i,1} + 0.1 f_{i,2} + e_{i,2}] \\ &= V[0.8 f_{i,1} + 0.1 f_{i,2}] + V[e_{i,2}] \\ &{\scriptsize(f_{i,1},f_{i,2}とe_{i,2}との独立性より)} \\[10px] \Rightarrow 1 &= \underbrace{\dfrac{V[0.8 f_{i,1} + 0.1 f_{i,2}]}{V[x_{i,2}]}}_{共通性} + \underbrace{\dfrac{V[e_{i,2}]}{V[x_{i,2}]}}_{独自性} \\ &= V[0.8 f_{i,1} + 0.1 f_{i,2}] + V[e_{i,2}] \\ &{\scriptsize(教科ごとに標準化されてるためV[x_{i,2}] = 1)} \\ &= (0.8^2 + 0.1^2) + V[e_{i,2}] \end{aligned}$$よって、上記の通りに数学の共通性・独自性は計算される。
(3).
Aさんは3人の中で、理系科目の点数が高く、文系科目の点数が低い。
よって、因子スコアの第1因子(『理系の能力の高さ』と解釈)が高く、第2因子(『文系の能力の高さ』と解釈)が低いものを選択すべきであり、$(1.2, -1.5)$が答えとなる。
例題2.
100人が5教科の体力テスト(ボール投げ、長距離走、ベンチプレス、遠泳、走り幅跳び)を行なった。
各体力テストについて標準化を行った上で、直交モデル・2因子モデルで解析をしたところ、(各因子に対する)因子負荷量の初期解は下記の通り得られた。
| 第1因子 | 第2因子 | |
| ボール投げ | 0.8 | 0.3 |
| 長距離走 | -0.5 | 0.3 |
| ベンチプレス | 0.9 | 0.2 |
| 遠泳 | -0.6 | 0.3 |
| 走り幅跳び | 0.7 | 0.4 |
この結果をプロットすると以下の様になる。
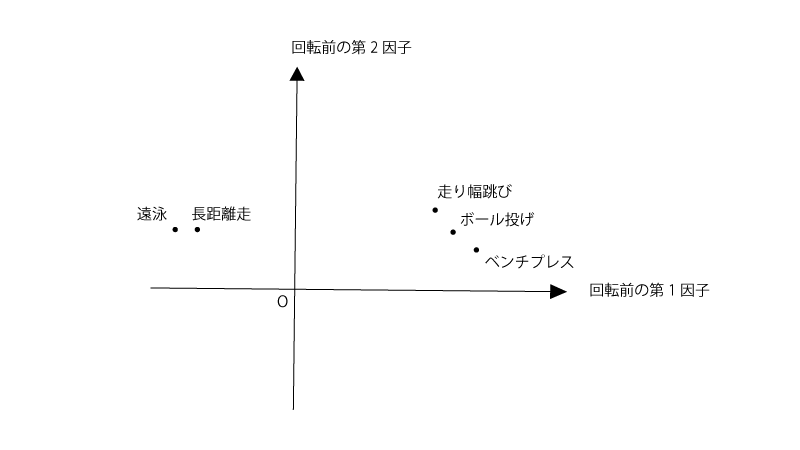
この状態と、直交回転ないし斜交回転をさせた後とで、いずれが最もよい解釈を与えるかをその理由とともに答えよ。
(回転させた後のプロットを自身で書いてみるとよい)
解答.
元々のプロットでは右側の3点、左側の2点は因子1ないし因子2の軸近くに存在していないが、回転をさせることでこれらの点を軸近くに存在させることができ、解釈性の向上につながる。
まず元のプロットを直交回転させると、以下の様なプロットになる。
(もちろんこのプロットのみが直交回転後の唯一のプロットではない)

3点は因子1の軸近くにのったが、2点は因子1ないし因子2の軸近くに存在してない。
そこで元のプロットを斜交回転させると、以下の様なプロットになる。
(もちろんこのプロットのみが斜交回転後の唯一のプロットではない)
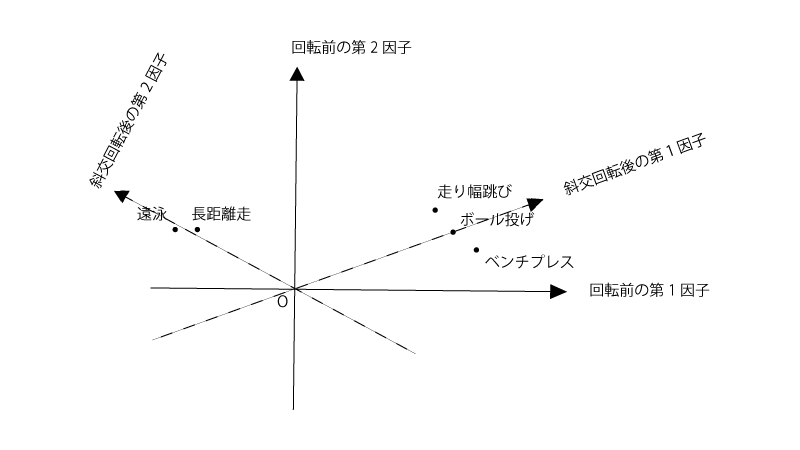
3点は因子1の軸近くにのり、2点は因子2の軸近くに存在する。
この時、因子1に対する因子負荷量はボール投げ、ベンチプレス、走り幅跳びで大きく、長距離走、遠投はほぼ$0$に近いところにある。
よって、因子1は『瞬発力』として解釈できる。
因子2に対する因子負荷量は長距離走、遠投で大きく、ボール投げ、ベンチプレス、走り幅跳びはほぼ$0$に近いところにある。
よって、因子2は『持久力』として解釈できる。
今回については、因子1『瞬発力』と因子2『持久力』とは多少相関があると想定されることから、元のプロットを斜交回転させることは不自然ではなく、回転後の各点が軸近くに存在することからは、この解釈性が最も高いと考えられる。
(注意:もちろん因子1,2の解釈は上記のみとは限らない)
例題3.
例題2の続きとして、元のプロットを斜交回転させたあとの因子1,2について、10人分のデータをプロットしたところ下記の様であった。
(例題2の段階では斜交回転後の2つの軸は直交していなかったが、例題3では見やすさを優先して直交させる形とした)
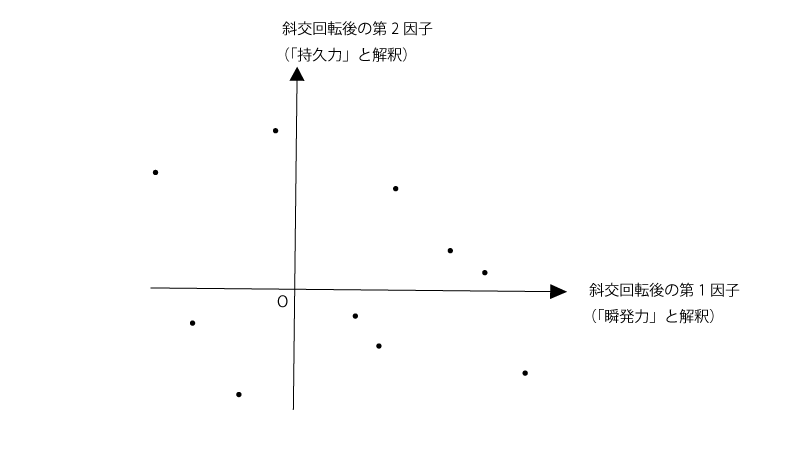
この10人のうちから短距離走にエントリーさせることにした。
誰が最も適しているか選択せよ。
解答.
短距離走では持久力は不要で瞬発力が求められるため*、因子2の大きさは関係なく因子1が最も大きい人を選ぶのが妥当である。
*:あくまで因子分析を理解するための極端な一例として例示したのでご理解ください。(つまり実世界では『短距離走では持久力は不要』ということはないのかもしれません)
例題2と例題3においてプロットがでてきましたが、その内容は異なることに気をつけてください。
例題2のプロットは元の変数5つの(第1因子・第2因子に対する)因子負荷量をプロットしたものなので、点は5個でした。一方で、例題3のプロットは第1因子・第2因子の値を人数分プロットしたものなので、点は10個でした。
その通りです。
まとめ.
- 因子分析とは、背景にあると想定できる変数を導く手法である。
- 制約条件のない因子分析モデルでは分布パラメータの解が一意に定まらないため、制約条件を課すことで、分布パラメータの一意な解(初期解)を求める。
- 得られた初期解の解釈が困難である場合には、回転させることで解釈性の向上を試みることができる。







