$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}} \\ \gdef \indep {\mathop{\perp\!\!\!\!\perp}} \\ \gdef \tr {\mathrm{tr}}$
SVM(Support Vector Machine)は機械学習の一種として耳にしたことがあります。
クラスの分類に使われる手法ですよね?
その通りです。
SVMとは『線形な分離境界』をを以てクラスの分類を行う手法です。
この『線形な』というところがミソになります。
というとどういうことでしょうか?
線形な分離境界とは、2次元でいうところの直線、3次元でいうところの平面になります。つまり曲線などは分離境界として用いません。
下記の様な感じですね。
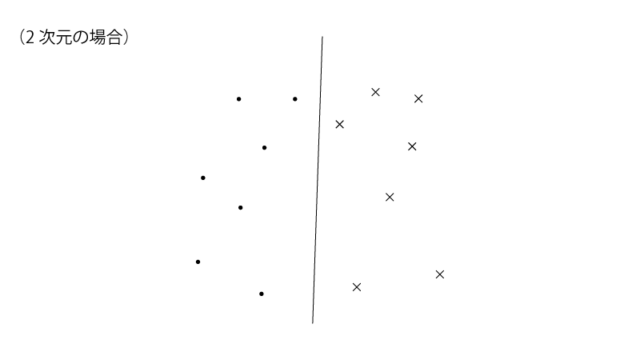
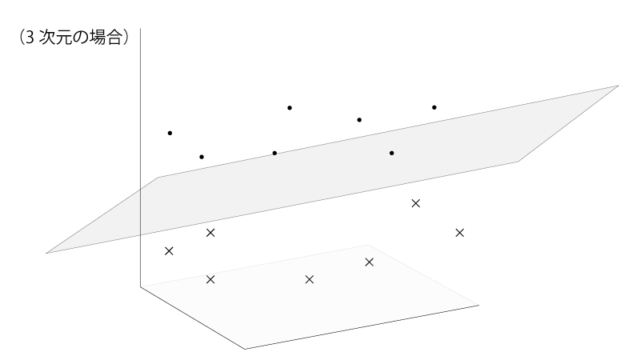
なるほど。でも思い返すと、下記の様に2次元のサンプルを円みたいな分離境界で分類しているものをみたことがあります。
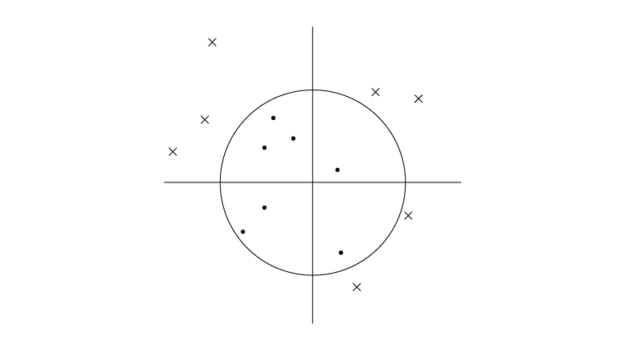
それはkernel SVMを用いたものでしょう。
kernel SVMではサンプルをより高次元の空間にうつした上で、線形な分離境界により分類します。
先の例では2次元のサンプルを3次元にうつした上で、平面により分類したわけです。それを2次元に戻してあげると円みたいな分離境界としてみえてたのです。
下記の様な感じですね。
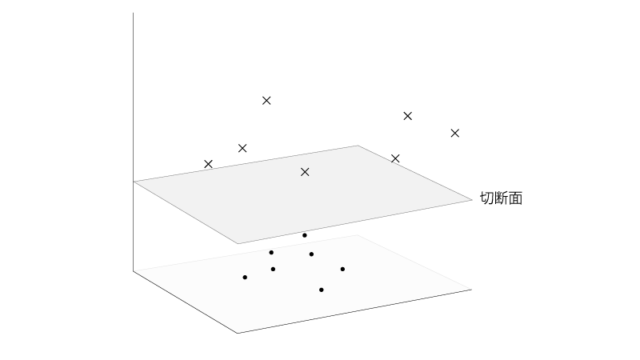
なるほど。SVMの分類では線形な分類境界しか使われない、というのはそういうことですね。
0. SVMの概略
SVMとは一言で言うと、線形な分離境界に基づくクラスの分類手法、です。
ここではSVMにおけるkey conceptsをまず紹介します。
0-1. 分離境界を設定する
SVMにおける分離境界は『線形な』ものに限定されます。
この分離境界の決定にあたっては、正しく各クラスを分離する分離境界のうち、「分離境界と各データ点との距離の最小値」を最大化するもの、が採用されます。
少し言い換えるなれば、分離境界と最も近いデータ点(”Support Vector“と言います)を考え、そのデータ点と分離境界との距離が最大となるもの、が選択されます。
実際の計算仮定ではありうる分離境界は無数ですが、仮に分離境界の候補が下記の様に①②のみとすると①が選択されます。
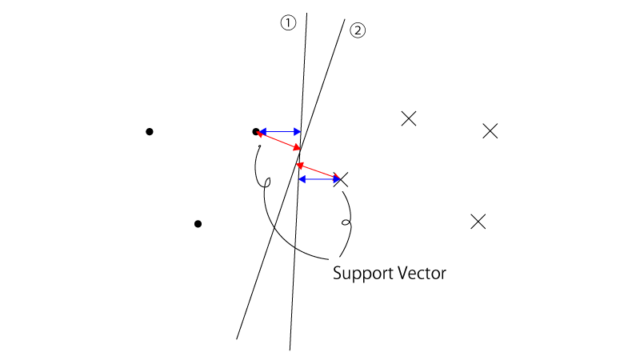
また分離境界の種類としてはhardなものとsoftなもの(それぞれ”hard margin“, “soft margin“と呼ばれることもあります)があります。
hardな分離境界はその分離境界の決定にあたって誤分類を許しませんが、softな分離境界はそれを許します。
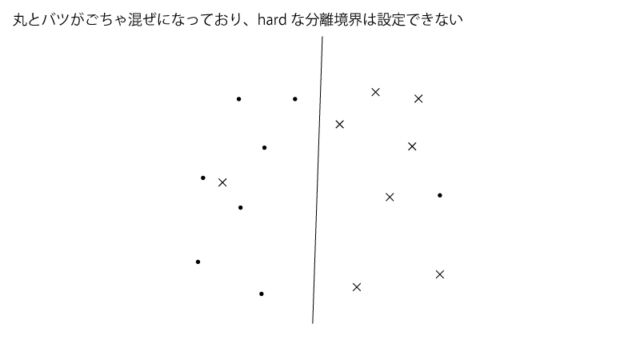
というのも下記の様な例ではhardな分離境界は設定することができず(うまく2クラスを分離する様な分離境界が存在しない)、softな分離境界のみが設定でき、この様な状況に対処するためにsoftな分離境界が準備されてると考えられます。また後出のkernel SVMを使えばhardな分離境界が準備できるとしても、その様にすると手元のデータにoverfitしてしまい汎化性能がよくなくなることがあります。
0-2. データ点をより高次元の空間に移す
例えば下記の様なケースではhardな分離境界は設定することができません。
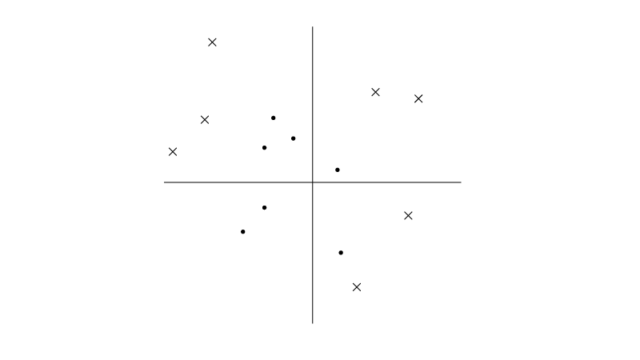
softな分離境界で許容するのも一つの手段ですが、分離性能がいまいちであれば使い道に乏しいです。
ここでデータ点をより高次元の空間に移してみると、
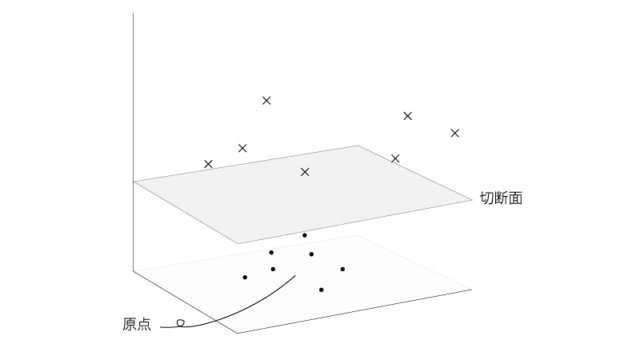
hardな分離境界も設定することができそうです。
SVMでは『分離境界を設定する』『データ点をより高次元の空間に移す』がkey conceptsです。
『データ点をより高次元の空間に移す』を適用しない場合を『1. SVM』で扱い、『データ点をより高次元の空間に移す』を適用する場合を『2. kernel SVM』で扱います。『1. SVM』『2. kernel SVM』ともにSVMの枠組みに含まれますが、『データ点をより高次元の空間に移す』というconceptを用いる場合を特に『kernel SVM』と言うわけです。なお、『分離境界を設定する』というconceptについては『1. SVM』『2. kernel SVM』どちらにも共通です。
1. SVM
先述の通り、2群を完全に分離する『hard margin SVM』と、誤分類を許す『soft margin SVM』との分けて話を進めます。
1-1. hard margin SVM
hard margin SVMは線形分離可能な場合にしか適用できないことに注意してください。
$p$次元のサンプル$\vec x_i (= (x_1, x_2, \cdots, x_p)^{\top}) ~~ \small{(i=1,\cdots,n)}$に対して、正解ラベル$y \in \{ -1, 1\}$が割り振られるものとします。$\vec w = (w_1, w_2, \cdots, w_p)^{\top}$に対して、識別関数$f(x)$を、
$$\begin{aligned} f(\vec x) = \vec w^{\top} \vec x + b \end{aligned}$$と定め、
・$f(\vec x_i) \gt 0 \Rightarrow$サンプル$i$のラベル$y_i$は1
・$f(\vec x_i) \lt 0 \Rightarrow$サンプル$i$のラベル$y_i$は-1
と識別するものとします。
すると、$f(\vec x)=0$が分離境界となるわけですが、この分離境界の決定(ひいては$f(\vec x)$の決定)に際しては、『各クラスを分離する様な分離境界のうちサンプルとの距離の最小値を最大化するもの、が選ばれます。
(『0-1. 分離境界を設定する』のFig参照)
つまり、
$$\begin{aligned} &\max_{\vec w, b} \min_{i=1,\cdots,n} \frac{| \vec w^{\top} \vec x_i + b |} {|| \vec w ||} ~~~~ s.t. ~~ y_i (\vec w^{\top} \vec x_i + b) \gt 0 ~~ \small{(i=1,\cdots,n)} ~~~~~ \mathrm{(A)^{(0)}} \end{aligned}$$という最適化問題$\mathrm{(A)^{(0)}}$を解くことになります。
$\frac{| \vec w^{\top} \vec x_i + b |} {|| \vec w ||}$は、$\vec x_i$と$f(\vec x) = 0$との距離ですね(高校数学)。
また、『サンプルiが正しく識別される』の必要十分条件は$y_i (\vec w^{\top} \vec x_i + b) \gt 0$であるため、これが制約条件になります。
$w_1, \cdots, w_p, b$を(同じ定数で)定数倍した時、最適化問題$\mathrm{(A)^{(0)}}$で最大化したい$\frac{| \vec w^{\top} \vec x_i + b |} {|| \vec w ||}$の分母・分子は同じ分だけ定数倍され打ち消し合います。
つまり、$w_1, \cdots, w_p, b$はスケーラブルであり、このままでは一意な解が求まりません。 そこで、
$$\begin{aligned} \min_{i=1,\cdots,n} | \vec w^{\top} \vec x_i + b | = 1 \end{aligned}$$という制約条件を最適化問題$\mathrm{(A)^{(0)}}$に追加します。
よって、
$$\begin{aligned} \max_{\vec w, b} \frac{1}{ || \vec w || } ~~~~ s.t. ~~ y_i (\vec w^{\top} \vec x_i + b) \geqq 1 ~~ \small{(i=1,\cdots,n)} ~~~~~ \mathrm{(A)^{(1)}} \end{aligned}$$という最適化問題$\mathrm{(A)^{(1)}}$を考えることになりますが、これは、
$$\begin{aligned} \min_{\vec w, b} \frac{1}{2} || \vec w ||^2 ~~~~ s.t. ~~ y_i (\vec w^{\top} \vec x_i + b) \geqq 1 ~~ \small{(i=1,\cdots,n)} ~~~~~ \mathrm{(A)^{(2)}} \end{aligned}$$という最適化問題$\mathrm{(A)^{(2)}}$と同等になります。
最適化問題$\mathrm{(A)^{(2)}}$で$|| \vec w ||^2$と$2$乗としたのは、$|| \vec w || = \sqrt{w_1^2 + \cdots + w_p^2}$とそのままではルートがついて計算が面倒であるためです。また最適化問題$\mathrm{(A)^{(2)}}$で$\frac{1}{2}$がついたのは後ほどの計算を楽にするためのものです。
結論を先に述べると、最適化問題$\mathrm{(A)^{(2)}}$で得られる最適解$\vec w$は、分離境界と最も近いデータ点(”Support Vector”)の線形結合で表され、つまり、
$$\begin{aligned} \vec w &= \sum_{i:\vec x_iはsupport ~ vector} \alpha_i y_i \vec x_i \end{aligned}$$となります。
(導出に興味がある方は以下の補足を参照ください)
これは、『$\small{(定数)} \cdot \vec x_i$』の足し合わせの形ですね。
そうですね。 これより識別関数$f(\vec x)$は、
$$\begin{aligned} f(\vec x) = \sum_{i:\vec x_iはsupport ~ vector} \alpha_i y_i \vec x_i^{\top} \vec x \end{aligned}$$となります。
補足. (SVMを初めて勉強している方は一旦ここを飛ばしていただいてよいかと思います)
ここでは最適化問題$\mathrm{(A)^{(2)}}$、即ち、
$$\begin{aligned} \min_{\vec w, b} \frac{1}{2} || \vec w ||^2 ~~~~ s.t. ~~ y_i (\vec w^{\top} \vec x_i + b) \geqq 1 ~~ \small{(i=1,\cdots,n)} ~~~~~ \mathrm{(A)^{(2)}} \end{aligned}$$を解いていきます。
制約条件が等式である時の最適化問題にはこれまでラグランジュの未定乗数法を用いてきましたが、制約条件が不等式である時にもこれと類似した手法を用います。
まず、ラグランジュ関数$L(\vec w, b, \vec \alpha)$を、
$$\begin{aligned} L(\vec w, b, \vec \alpha) = \frac{1}{2} || \vec w ||^2 + \sum_i \alpha_i \{ 1-y_i (\vec w^{\top} \vec x_i + b) \} \end{aligned}$$と定めます。
すると、最適解は以下の条件(『KKT条件』と言います)を満たします。
①
$$\begin{aligned} \frac{\partial L}{\partial \vec w} = 0 &\Leftrightarrow \vec w-\sum_i \alpha_i y_i \vec x_i = 0 \\[10px] &\Rightarrow \vec w = \sum_i \alpha_i y_i \vec x_i \end{aligned}$$
②
$$\begin{aligned} \frac{\partial L}{\partial b} = 0 &\Leftrightarrow -\sum_i \alpha_i y_i = 0 \\[10px] &\Rightarrow \sum_i \alpha_i y_i = 0 \end{aligned}$$
③
$$\begin{aligned} y_i (\vec w^{\top} \vec x_i + b) \geqq 1 ~~ \small{(i=1,\cdots,n)} \end{aligned}$$
④
$$\begin{aligned} \alpha_i \geqq 0 ~~ \small{(i=1,\cdots,n)} \end{aligned}$$
⑤
$$\begin{aligned} \alpha_i \{ 1-y_i (\vec w^{\top} \vec x_i + b) \} = 0 \end{aligned}$$
①②はラグランジュの未定乗数法でもでてきたものですね。
③は既出の制約条件そのまんまです。
ただ、④⑤はラグランジュの未定乗数法ではでてこず既出の制約条件でもないですね。
既出の制約条件である③が不等式であるために課された、係数についての制約条件が④になります。⑤は$\sum$の中身が$0$というもので、『相補性条件』と呼ばれるものです。
①の、$\vec w = \sum_i \alpha_i y_i \vec x_i$、からは$\vec w$はすべてのデータ点から決まる様に思いますが、$\alpha_i=0$であるデータ点は寄与しません。
$\alpha_i=0$と限らないのは、⑤より$y_i (\vec w^{\top} \vec x_i + b) = 1$を満たすデータ点です。
これは、完全に分離されてることに対する不等式制約(③)の等号が成立するデータ点、即ち、分離境界に最も近いデータ点となります。
まとめると最適解$\vec w$は、分離境界に最も近いデータ点(”Support Vector”)を用いて、
$$\begin{aligned} \vec w &= \sum_{i:\vec x_iはsupport ~ vector} \alpha_i y_i \vec x_i \end{aligned}$$となります。
1-2. soft margin SVM
soft margin SVMでは誤分類を許容し、誤分類をした場合には非負の罰則$\xi_i$を加えます。
よって、最適化問題$\mathrm{(A)^{(2)}}$に対応する最適化問題は、
$$\begin{aligned} &\min_{\vec w, b} \frac{1}{2} || \vec w ||^2 + C \sum_{i=1}^n \xi_i ~~~~~ \mathrm{(A)^{(2)}} \\[10px] &s.t. \begin{cases} y_i (\vec w^{\top} \vec x_i + b) \geqq 1-\xi_i ~~ \small{(i=1,\cdots,n)} \\ \xi_i \geqq 0 \\ C \gt 0 \end{cases} \end{aligned}$$となります。
$C$は罰則の大きさを制御する定数であり、$C$が大きいほど誤分類をした時の罰則が大きくなり、$C$が小さいほど誤分類をした時の罰則が小さくなります。
また最適解の下では$\xi_i$は、
$$\begin{aligned} \xi_i &= \max \{ 1-y_i f(\vec x_i), 0 \} \\ &{\scriptsize(f(\vec x)=\vec w^{\top} \vec x + b、は識別関数でした)} \end{aligned}$$となり、Figとして表すと以下の様になります。
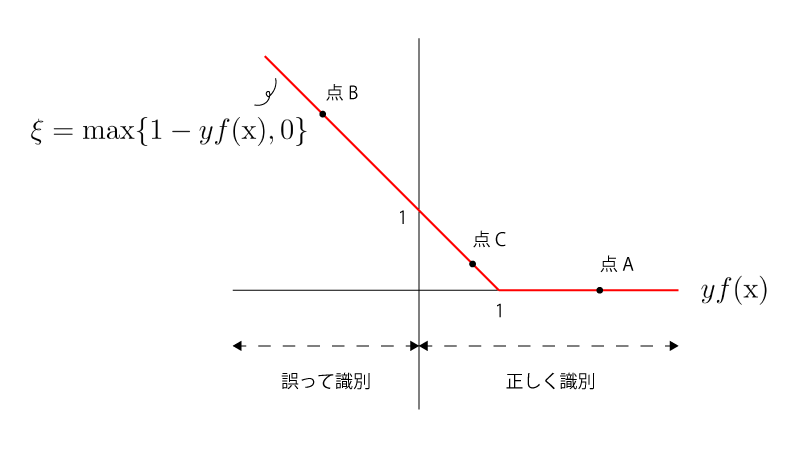
点Aは正しく分類できていて罰則がないですね。
点Bは誤分類していて罰則がありますね。
点Cは正しく分類できているにも関わらず、罰則がありますね。
あれ、誤分類をした時のみ罰則があるのではないのですか?
実はそういうわけではないのです。
誤分類をした時に罰則があるのは間違いないですが、正しく分類した時にも罰則が与えられることがあります。(点C)
この点注意をしてください。
2. データ点をより高次元の空間に移すkernel SVM
『0-2. データ点をより高次元の空間に移す』で紹介した例の様に、データ点をより高次元の空間に移すことで、SVMによるより良い分類が可能になることがあります。
各データ点$\vec x_i ~~ \small{(i=1,\cdots,n)}$に対して関数$\phi$をかませた$\phi(\vec x_i)$を考えることで、データ点をより高次元の空間に移すことができます。
2-1. hard margin SVM
前出の最適化問題$\mathrm{(A)^{(2)}}$に対応する最適化問題は、
$$\begin{aligned} \min_{\vec w, b} \frac{1}{2} || \vec w ||^2 ~~~~ s.t. ~~ y_i (\vec w^{\top} \textcolor{red}{\phi(\vec x_i)} + b) \geqq 1 ~~ \small{(i=1,\cdots,n)} \end{aligned}$$となります。($\vec x_i$が$\phi(\vec x_i)$に置換されただけです)
最適解$\vec w$は上記同様に、
$$\begin{aligned} \vec w &= \sum_{i:\textcolor{red}{\phi(\vec x_i)}はsupport ~ vector} \alpha_i y_i \textcolor{red}{\phi(\vec x_i)} \end{aligned}$$となります。
最適解の形がわかったので、これを元の最適化問題に代入すると、
$$\begin{aligned} &\min \frac{1}{2} \sum_{i,j} \alpha_i \alpha_j y_i y_j \phi(\vec x_i)^{\top} \phi(\vec x_j) \\[10px] ~~~~ &s.t. ~~ y_i (\sum_j \alpha_j y_j \phi(\vec x_j)^{\top} \phi(\vec x_i) + b) \geqq 1 ~~ \small{(i=1,\cdots,n)} \end{aligned}$$となりますが、$\phi (\vec x)$は$\phi (\vec x)^{\top} \phi (\vec x’)$という内積の形で必ず出現してます。
そのため、$\phi (\vec x)$を直接的に定めなくとも$\phi (\vec x)^{\top} \phi (\vec x’)$を定めることで境界を求めることが可能です。
この様に$\phi (\vec x)$を直接的に定めず$\phi (\vec x)^{\top} \phi (\vec x’)$を定めることで境界を決められるというトリックを『カーネルトリック』と言います。
なお、$k(\vec x, \vec x’) = \phi (\vec x)^{\top} \phi (\vec x’)$、を『カーネル関数』と呼びます。
なるほどです。ただこのトリックのよい点をよくわかっていません。。
$\phi (\vec x)$は高次元ですが$\phi (\vec x)^{\top} \phi (\vec x’)$は1次元になってますね。カーネル関数を考えることで間接的に高次元空間上での分類が可能になりますが、高次元の写像を明示的に計算する必要がなくなるため計算量的に楽になります。
$\phi (\vec x)$を個別に準備するとそれ自体に高次元の計算が必要となり、さらには内積計算$\phi (\vec x)^{\top} \phi (\vec x’)$をする必要があります。一方で、カーネル関数$\phi (\vec x)^{\top} \phi (\vec x’)$自体を準備することでこれらの高次元の計算や内積計算を省くことができるという理解でしょうか?
その通りです!なお、カーネル関数はどの様なものでも許されるわけではありませんが、以下補足にあるメジャーな3種類を押さえておけば問題ありません。
補足.
カーネル関数$k(\vec x, \vec x’) = \phi (\vec x)^{\top} \phi (\vec x’)$の種類はたくさんありますが、よく使用されるのは以下の3種類です。
・①『線形カーネル』
$k(\vec x, \vec x’) = \vec x^{\top} \vec x’$
これは通常のSVM(kernel SVMではなく)に出てくる形そのままです。
・②『多項式カーネル』
$k(\vec x, \vec x’) = (\vec x^{\top} \vec x’ + C_0)^d ~~ \small{(C_0 \geqq 0, d \in \mathrm{\vec N})}$
(参照:赤穂 昭太郎『カーネル多変量解析』岩波書店, 2008)
・③『ガウシアンカーネル』
$k(\vec x, \vec x’) = \exp [-\sigma || \vec x-\vec x’ ||^2]$
①〜③それぞれを用いてみると分離境界の様子も異なることがわかります。
なお、下記はこちらのページを改変したもので、irisというデータセットをもとにしてます。
横軸に花の萼の長さ、縦軸にその幅がプロットされてます。
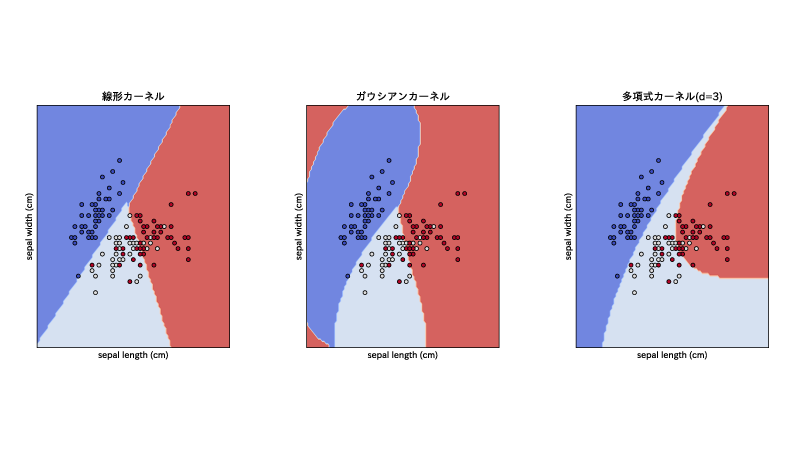
線形カーネルは分離境界が直線に見えますが、ガウシアンカーネルと多項式カーネルでは曲線に見えますね。
2-2. soft margin SVM
こちらは1-1が2-1にmodifyされたように、1-2が2-2にmodifyされるだけなので省略します。
例1.
以下はkernel SVM(ガウシアンカーネル) > soft margin SVM、の例である。
日本の野球選手、バスケットボール選手の身長、体重を標準化したものがプロットされており、罰則項である$C$を変化させている。
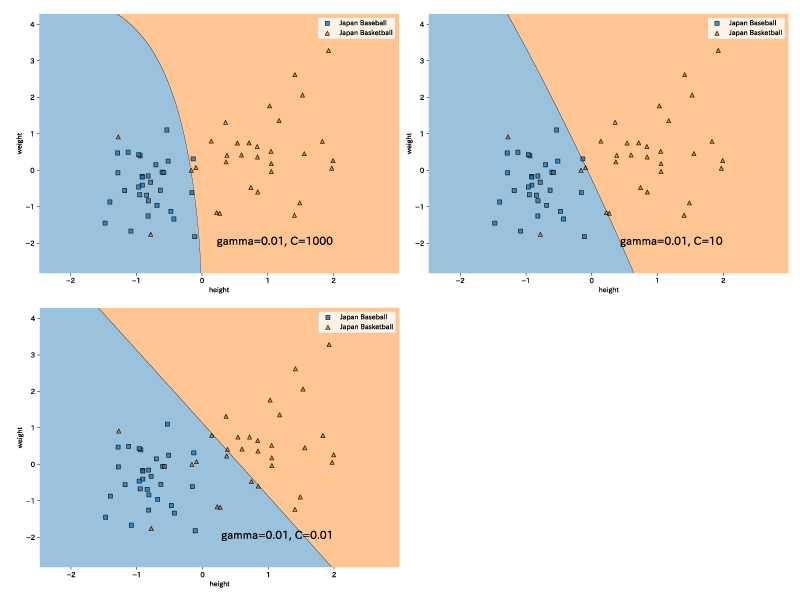
罰則項$C$が大きいほど誤分類した場合の罰則が大きくなってしまうため、罰則項$C$が大きいほど誤分類しないように分離境界が設定されているように見えます。
罰則項$C$は大きすぎると手元のデータにoverfitし汎化性能が良く無くなることが多いです。
一般には手元のデータからSVM学習機を作成し、それを別のデータに適用することでクラスの分類をしますが、もしも別のデータが手元のデータに類似していると想定されて、高い判別性能を達成したければ罰則項$C$はある程度大きくすればよいのです。 一方でもしも別のデータが手元のデータに類似しているとは想定されず、それでもなおある程度の判別性能を達成したければ罰則項$C$はある程度小さくすればよいのです。
まとめ.
- SVMとは『線形な分離境界』をを以てクラスの分類を行う手法である。
- 誤分類を許容しないhard margin SVMと、許容するsoft margin SVMとに分けられる。soft margin SVMでは誤分類をした際に罰則が与えられるが、罰則の大きさを制御する罰則項$C$は文脈に応じて決める必要がある。
- データ点をより高次元の空間に移すkernel SVMもある。 kernel SVMではカーネル関数を考えることで計算コストを抑えている。









