$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}} \\ \gdef \indep {\mathop{\perp\!\!\!\!\perp}} \\ \gdef \tr {\mathrm{tr}}$
今回はサンプリング法の最も基本的手法である『逆関数法』を扱います。
サンプリング法自体に馴染みがないので難しそうですね。。
初めて聞くとそう感じてしまうかもしれませんが、道具としては「分布関数の逆関数」「一様分布」を使うのみであり、シンプルな手法です。
1. 逆関数法
確率変数$X$の分布関数をそれぞれ$F_X (x)$とします。
この時、$F_X (x)$の逆関数$F_X^{-1} (u)$が陽に得られる場合、以下のstepにより$F_X(x)$に従う乱数を生成することができます。
step1) 一様分布$\U(0,1)$から乱数$u$を得る
step2) $x’ = F_X^{-1} (u)$として$x’$を生成する
このstepにより生成された$x’$が$F_X(x)$に従うことは、
$$\begin{aligned} Pr \{ F_X^{-1} (U) \leqq x’ \} &= Pr \{ U \leqq F_X(x’) \} \\ &= F_X(x’) \end{aligned}$$から確認できます。
補足.
初めて逆関数法を知った方はイメージが湧いてないかもしれません。
そこで、とある分布を例に逆関数法についてのイメージを確認しておきます。
最終目的としては以下の様にとある分布に従う乱数を得ることです。
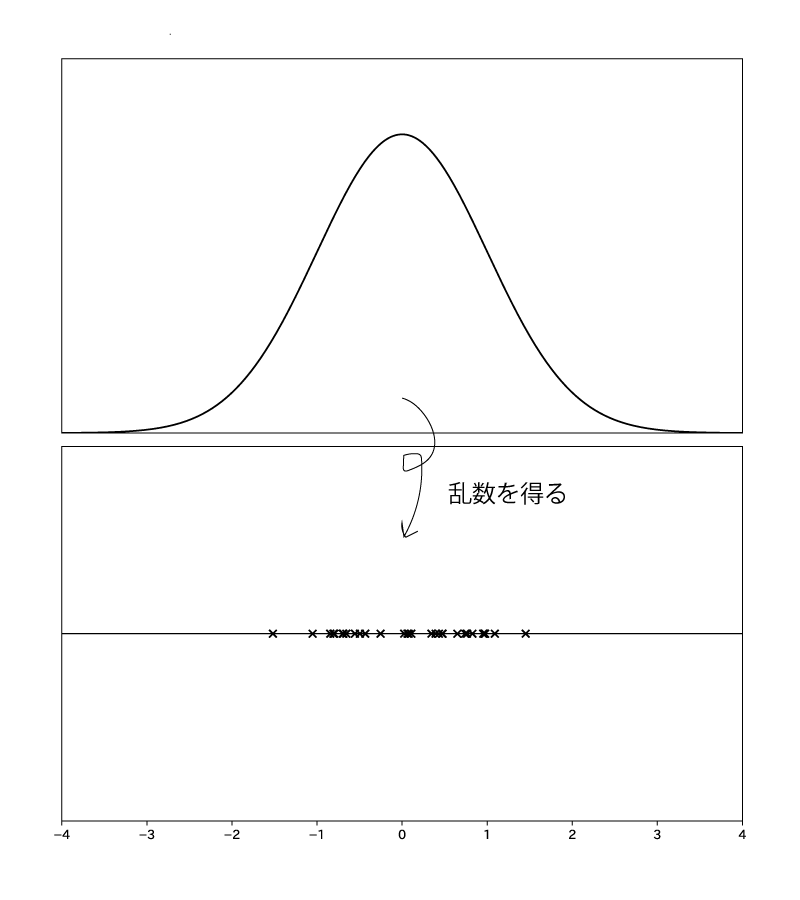
この分布の分布関数は以下の様になります。
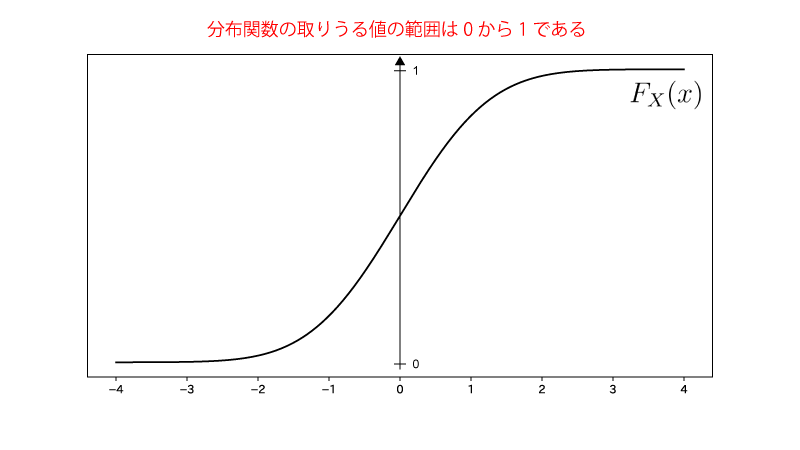
ここで、$u \sim \U[0,1]$、という乱数を得た上で、$F_X^{-1} (u)$を生成すると、
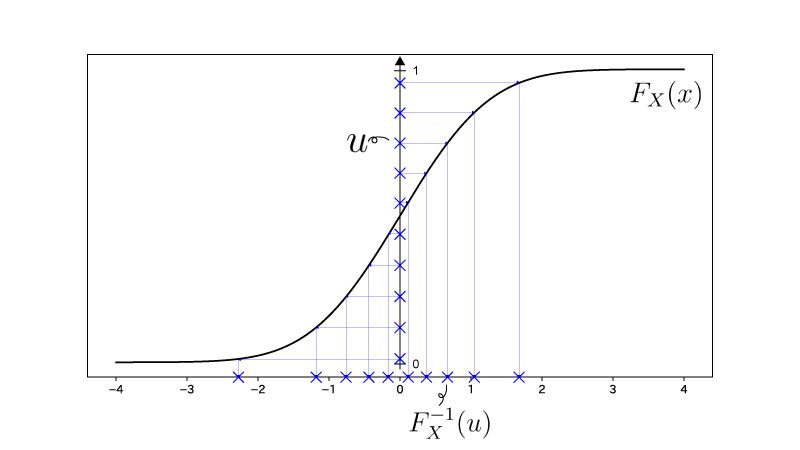
この様に得たい乱数が得られるわけです。
このFiguresのイメージを持っておけば逆関数法は問題ないでしょう。
例題1.
指数分布$\Exp(\lambda)$に従う乱数100個を逆関数法で生成したい。
その流れを具体的に説明せよ。
解答.
$\Exp(\lambda)$の確率密度関数、分布関数をそれぞれ$f_X(x), F_X(x)$とすると、
$$\begin{aligned} f_X(x) &= \lambda e^{-\lambda x} ~~~~~ \small{(x \gt 0)} \\[10px] F_X(x) &= \int_0^x \lambda e^{-\lambda t} dt \\[10px] &= [-e^{-\lambda t}]_0^x \\[10px] &= 1-e^{-\lambda x} \end{aligned}$$
$F_X (x)$の逆関数$F_X^{-1} (u)$は、
$$\begin{aligned} F_X^{-1} (u) = -\frac{1}{\lambda} \log (1-u) ~~~~~ \small{(0 \lt u \leqq 1)} \end{aligned}$$なので、以下のstepにより$\Exp(\lambda)$に従う乱数を生成することができる。
step1) 一様分布$\U(0,1)$から乱数$u$を100個得る
step2) $x’ = F_X^{-1} (u) = -\frac{1}{\lambda} \log (1-u) ~~~~~ \small{(0 \lt u \leqq 1)}$として$x’$を100個生成する
注意.
$U \sim \U[0,1]$である時、$1-U \sim \U[0,1]$であるため、step2について、『$x’ = -\frac{1}{\lambda} \log (u) ~~~~~ \small{(0 \leqq u \lt 1)}$として$x’$を100個生成する』としても構いません。
まとめ.
- 逆関数法とはサンプリング法のうち最も基本的な手法である。
- 逆関数法の具体的な流れを一言でまとめると、『分布関数の逆関数を以て、一様分布に従う乱数を変換する方法』である。




