簡単に私と本サイトについて紹介します。
0. ABOUT すたどく
- 医師(東京大学医学部医学科卒)
- ビッグデータを用いた医学研究や画像解析研究をしています
1. データで溢れる社会にどう立ち向かうのか? 〜統計学を学ぶ理由〜
1-1. すでにデータで溢れる社会がますますデータで溢れていく
「IoT(Internet of things)」という言葉を耳にされたことがあるかと思います。
元々はコンピュータ同士をつなげるためのものであったインターネットが、あらゆる『モノ』をつなげ情報網を形成する、というのが「IoT」です。
IoTを一端として今後あらゆる『モノ』が情報収集/伝達のハブと化し、社会のデータ量が増え続けていくことはほぼ間違いありません。
社会のデータ量が増えることでよりよい社会となることが期待されますが、果たして溢れるデータを有効に処理しきれるのか不安が抱かれます。
1-2. ビッグデータの高速処理が可能となった
近年のパソコン(学習器)の計算能力の向上により、いわゆる「ビッグデータ」を高速処理できるようになりました。
ビッグデータを解析する手法は様々ですが、機械学習や深層学習(ディープラーニング)といった比較的新しい手法が世間の注目を集め、2022年現在では初学者でも比較的簡単にこれらの手法をはじめとした解析手法を勉強し実践できる環境が整っています。
ビッグデータの解析手法が世間に広く認知されることは素晴らしいことですが、素地をないがしろにして解析をしてしまうことで、誤った結論を導いてしまうことが懸念されます。
1-3. データを『正しく』解析することは難しい
身の回りのデータ量が増えそれを解析する手法も浸透してきましたが、そもそもデータを『正しく』解析することは非常に難しいことです。
基本的な解析手法である線形回帰を題材に、単純な例を1つ挙げます。
ある病気での入院日数とBMI(グループ1:17.5以上20.0未満、グループ2:20.0以上22.5未満、グループ3:22.5以上25.0未満、グループ4:25.0以上27.5未満、グループ5:27.5以上30.0未満)の関係性を、各グループからの代表30人ずつのデータを以て解析するとします。
データをプロットしてみると以下のFig1の様になりました。
Fig1

「線形回帰モデル」というモデルがあるのを知った過去の私は、入院日数を被説明変数、BMIをグループごとに1, 2, 3, 4, 5と連続変数として説明変数とした線形回帰モデルで解析しました。
すると、BMIの回帰係数は+2(つまり、グループ1→2→3→4→5となるにつれて入院日数が平均2日ずつ増えていく)という結果が得られました。
果たしてこの解析は『正しい』ものでしょうか?
結論として、線形回帰モデルの仮定を知らずに行われたこの解析は『正しい』とは言い難いです。
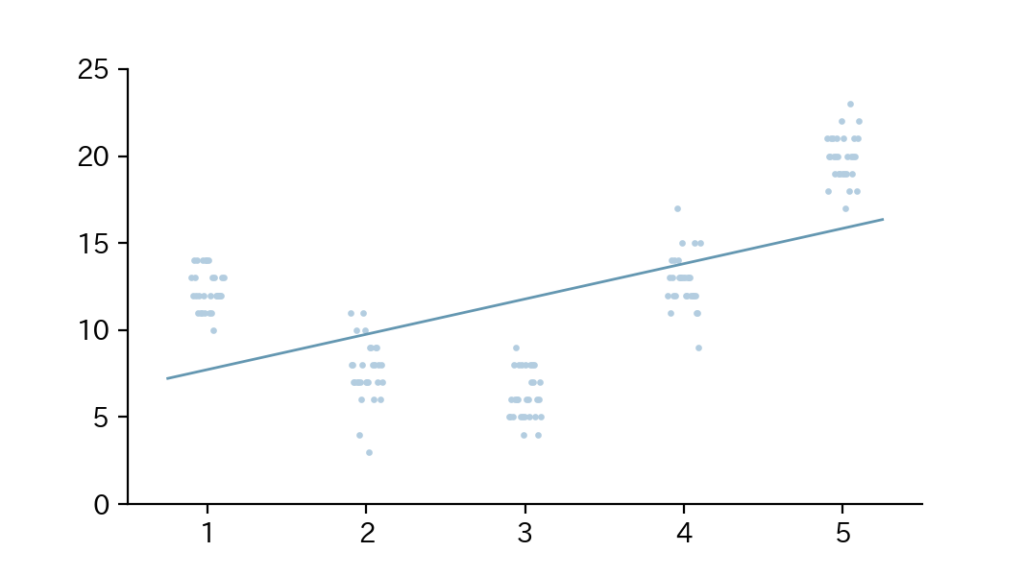
というのも、線形回帰では『説明変数(連続変数)と被説明変数(連続変数)との平均的な関係は1本の直線で表現される』という仮定がおかれており(統計学の知識)、このおわん型のデータに対してこの仮定を適用するのはやや無理がありそうだからです。
(仮定が成り立つとした解析はFig2のように1本の青線を引くことに相当します。またそもそも順序尺度をナイーブに連続尺度に変換してしまってよいのかという問題もあります。)
Fig2
線形回帰が前提とする仮定が妥当であるかを判断するにあたって、本来は目の前のデータのみならず先行研究など(統計学以外の知識)も参照する必要があります。
つまりは、目の前のデータのみから『絶対的に正しい』解析を一律に決めることは不可能なのです。
(そもそも『絶対的に正しい』解析とは先行研究などがあったとしても決め難いものです)
しかしながら、そもそもの線形回帰が前提とする仮定を知らずにそれを実践してしまう人は、『相対的に正しくない』解析をしてしまう可能性が高いことには疑いの余地がありません。
『相対的に正しくない』解析をしてしまわないようにするためには様々な知識が要求されますが、そのひとつの核となるのは統計学です。
2. 本サイトについて
2-1. 大枠
私は研究者としてペーペーではありますが、研究に携わろうと決めた段階から統計学の勉強をしてきました。
解析のやり方のみを手っ取り早く習得するだけでは、『相対的に正しくない』解析をしてしまうのではないかと直観的に恐れたためです。
実際に、統計学を勉強してきたことで『相対的に正しくない』解析を避けることに役立ってきたと実感しています。
本サイトでは、私が勉強しまとめてきた統計学の内容をシェアしていきたいと思います。
2-2. 具体的に
本サイトでは統計学の主な教材として『統計検定』を採用しています。
『統計検定』は日本統計学会が公認する検定で、統計に関する知識や活用力を問うものです。
いくつかの級に分かれますが、各級のカバーする知識・内容(私の所感としては)以下のとおりです。
- 2級:データを『正しく』解析しようとする人にとって必須となる知識
- 準1級:データ解析でよく使われる統計解析手法を幅広く含んだ内容(実践を意識)
- 1級:基本的な統計学の内容を理論から問いかける内容(理論を意識)
私の場合には統計学を勉強し始めた当時は2級の範囲もおぼつきませんでしたが、勉強を継続することで1級まで取得し、さらなる統計学の勉強や研究に役立てられています。
どのレベルから扱うべきか悩みましたが、1級の内容をわかりやすく扱うサイト・書籍が少ないことから、まずは1級の内容を扱うことにしました。
内容は1級合格に足る様に、そして可能な限りわかりやすくまとめていきます。
2-3. 今後
統計学の内容から充実を図り、余裕がでてくればその他コンテンツ(データ解析をする際に知っておくべき一般的事項、統計ソフトの使い方など)も追加していきたいと思います。
どうぞよろしくお願いします。
2-4. サポーター
本サイトの作成にあたり統計学に明るい友人2人に原稿の確認・助言をお願いしています。
ここに感謝の意を表します。
PS.
横長の式の場合にはスマホやタブレットではずれが生じうるので、パソコンで見ていただくことをお勧めします。
2022/09/07 すたどく
