ログランク検定とCox比例ハザード解析の違いの整理

$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}} \\ \gdef \indep {\mathop{\perp\!\!\!\!\perp}} \\ \gdef \tr {\mathrm{tr}}$

以下ではログランク検定、Cox比例ハザード解析の違いを、2つの観点：①モデルの構造、②複数の説明変数をモデルに組み込むことができるか？、から整理していきます。

1. モデルの構造

それぞれのモデルの構造は、

⚫️ログランク検定のモデル：ノンパラメトリックモデル
⚫️Cox比例ハザード解析のモデル：セミパラメトリックモデル

となります。




ここでノンパラメトリックモデルとパラメトリックモデル（セミパラメトリックモデルではなく）の利点・欠点を復習しましょう。

	利点	欠点
ノンパラメトリック	– 分布・モデルを指定しないので常に使える　　　　　　 – 分布・モデルの誤設定の心配がない	– 分布・モデルを指定しないことで検出力が低下する可能性がある
パラメトリック	– 分布・モデルを指定するため検出力が向上する可能性がある	– 分布・モデルを指定する必要があるため常に使えるとは限らない （適した条件下でしか使えない） – 分布・モデルの誤設定の心配がある

2. 複数の説明変数をモデルに組み込むことができるか？

結論からすると、

⚫️ログランク検定のモデル：複数の説明変数をモデルに組み込むことができない
⚫️Cox比例ハザード解析のモデル：複数の説明変数をモデルに組み込むことができる

となります。




例として、イベントを『死亡』として、治療薬A、プラセボ薬Bによる生存時間解析を扱います。 以下の様なカプランマイヤー曲線が与えられたとします。

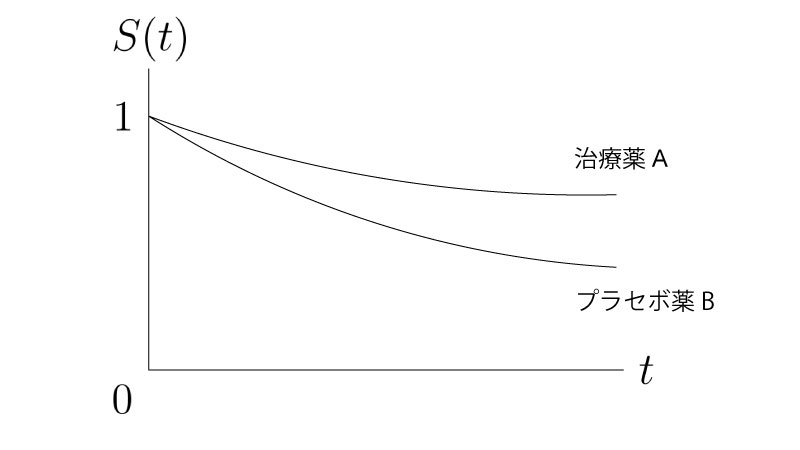
ログランク検定では＜カプランマイヤー推定量・曲線とログランク検定＞で扱った通り、上のカプランマイヤー曲線上にあるデータから検定統計量を構成し、それに基づいた検定をします。


複数の説明変数をモデルに組み込むことができないため、例えば年齢カテゴリー(65歳以上、65歳未満)によって調整したいと思ってもそれはできません*。
（*：ただし、年齢カテゴリーによって層別化すれば年齢カテゴリーによる生存関数の違いを確認することは可能です）




一方のCox比例ハザード解析では、説明変数$x_{i,1} (= 1 \small{(治療薬A)}$, $0 \small{(プラセボ薬B)})$を用いてハザード関数$h(t;x_{i,1}) = h_0 (t) \cdot \exp (\beta_1 x_{i,1})$と置いた上で、回帰係数$\beta_1$の検定がなされます。


別の説明変数として例えば年齢、性別が生存時間に影響していると考えた時、$x_{i,2} (= 1 \small{(65歳以上)}$, $0 \small{(65歳未満)})$, $x_{i,3} (= 1 \small{(男性)}$, $0 \small{(女性)})$などと設定し、$h(t;\vec x_i) = h_0 (t) \cdot \exp (\beta_1 x_{i,1} + \beta_2 x_{i,2} + \beta_3 x_{i,3})$と置いた上で、回帰係数$\beta_1$の検定がなされます。


この、年齢、性別を組み込んだ解析では、年齢、性別を調整したものと考えられます。 即ち、年齢、性別を調整した上での、プラセボ薬Bに対する治療薬Aの効果を見ることができます。