$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}} \\ \gdef \indep {\mathop{\perp\!\!\!\!\perp}} \\ \gdef \tr {\mathrm{tr}}$
『判別分析』についての知識が全くないのですが、これはどういった手法でしょうか?
『判別分析』とは、入力された特徴量を以てクラスを判別する手法です。
具体的に、既存のサンプル(10匹の猫、10匹の犬)についてある特徴量(ヒゲの長さ、胴体の長さ、足の長さ)のデータがあるとします。
この時新たなサンプルについての特徴量が与えられたとして、このサンプルが猫か犬かを判別するといった具合です。
なるほどです。
具体的な判別の流れはどうなりますか?
以下の流れになります。
step 1. 既存のサンプルについての特徴量から射影軸を決定する
step 2. 新たなサンプルについての特徴量をその射影軸に射影する
step 3. 2で射影されたものと、各クラスの射影軸上の平均とを比較して、最も近くのクラスに判別する
1.(Fisherの)(線形)判別分析、2クラス
1-1. 判別分析の流れのイメージを掴む
既存のサンプル(10匹の猫、10匹の犬)についてある特徴量(ヒゲの長さ、胴体の長さ、足の長さ)のデータがあるとします。
この時新たなサンプルについての特徴量が与えられたとして、このサンプルが猫か犬かを判別します。
判別分析の流れは各stepに従います。
step 1. 既存のサンプルについての特徴量から射影軸を決定する
step 2. 新たなサンプルについての特徴量をその射影軸に射影する
step 3. 2で射影されたものと、各クラスの射影軸上の平均とを比較して、最も近くのクラスに判別する
下記でそれぞれのstepのイメージを掴みましょう。
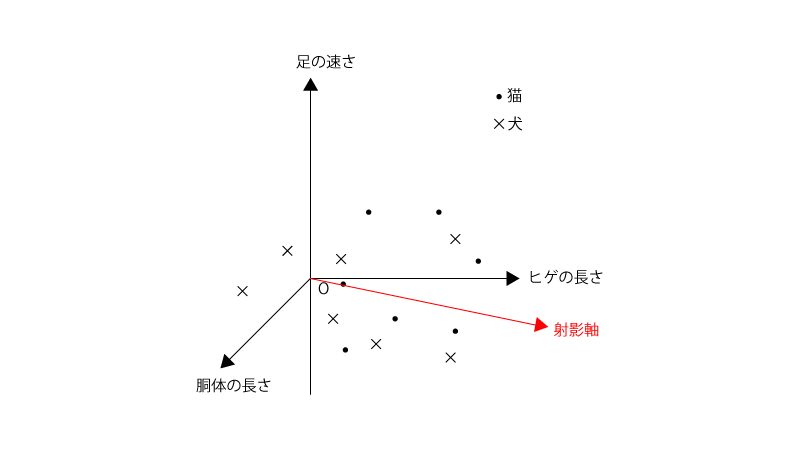
●step 1. 既存のサンプルについての特徴量から射影軸を決定する
既存のサンプルについての特徴量から赤色の様な射影軸を1つ決定します。
この射影軸の決定の仕方は『1-2. 射影軸の決め方』で具体的に扱いますが、射影軸に投影した後の各クラス内での分散が小さく、各クラス間での『キョリ』が大きくなる様に決定されます。
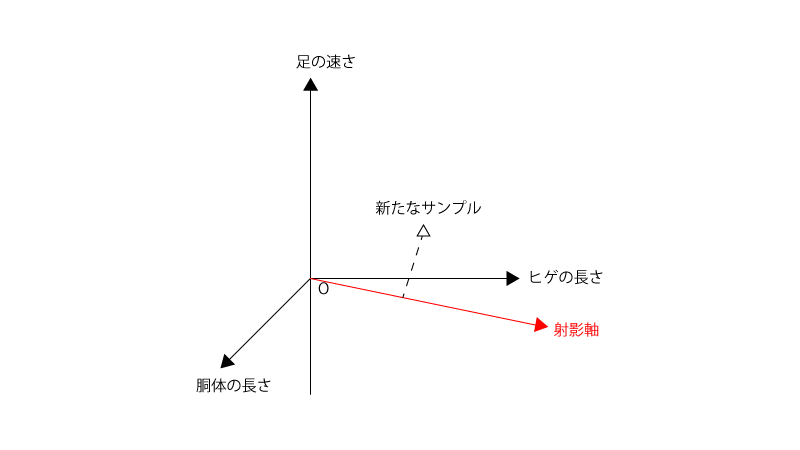
●step 2. 新たなサンプルについての特徴量をその射影軸に射影する
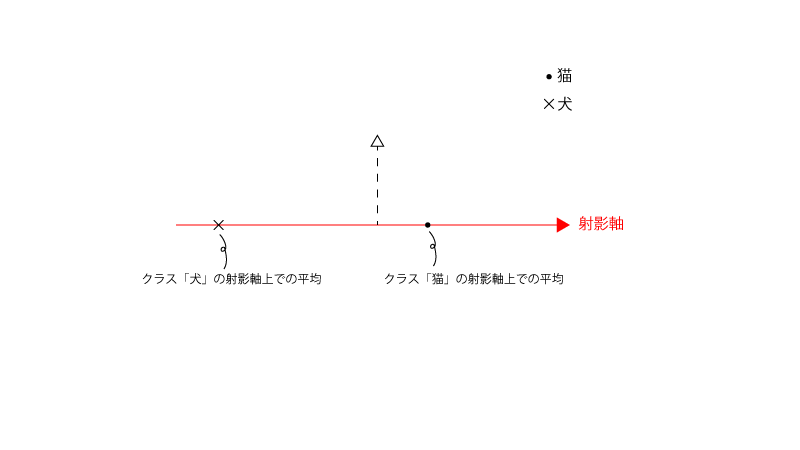
●step 3. 2で射影されたものと、各クラスの射影軸上の平均とを比較して、最も近くのクラスに判別する
以下の様な場合は新たなサンプルは●(猫)に判別されます。
1-2. 射影軸の決定(計算)
$p$次元の特徴量データ$\vec x_i^{(1)}, \vec x_j^{(2)} ~~\small{(i=1,\cdots,n_1; j=1,\cdots,n_2)}$があるとします。
($\vec x_i^{(1)}, \vec x_j^{(2)}$それぞれが「猫」「犬」を表すイメージです)
射影軸を決定するにあたっては、射影後の郡内変動に対して射影後の郡間変動を最大化する様なものが選択されます。
即ち、射影軸に沿ったベクトルの1つを$\vec w$とした時、
$$\begin{aligned} \sum_{i=1}^{n_1} (\vec w^{\top} \vec x_i^{(1)}-\vec w^{\top} \bar{\vec x}^{(1)})^2 + \sum_{j=1}^{n_2} (\vec w^{\top} \vec x_j^{(2)}-\vec w^{\top} \bar{\vec x}^{(2)})^2 \end{aligned}$$に対して、
$$\begin{aligned} (\vec w^{\top} \bar{\vec x}^{(1)}-\vec w^{\top} \bar{\vec x}^{(2)})^2 \end{aligned}$$を最大化する様なものが選択されます。
一般に下記の郡内変動行列$S_w$、群間変動行列$S_B$($w$:within、$B$:between)を準備すると、($S_w$は通常正則であり、ここでも正則であるものとする)
$$\begin{aligned} S_w &= \sum_{i=1}^{n_1} ( \vec x_i^{(1)}-\bar{\vec x}^{(1)} ) ( \vec x_i^{(1)}-\bar{\vec x}^{(1)} )^{\top} + \sum_{j=1}^{n_2} ( \vec x_j^{(2)}-\bar{\vec x}^{(2)} ) ( \vec x_j^{(2)}-\bar{\vec x}^{(2)} )^{\top} ~~~~~ \mathrm{(A)} \\[10px] S_B &= (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)}) (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)})^{\top} ~~~~~ \mathrm{(B)} \end{aligned}$$上記で紹介した内容は、
$$\begin{aligned} \mathrm{maximize} \frac{ \vec w^{\top} S_B \vec w }{ \vec w^{\top} S_w \vec w } \end{aligned}$$とも書くことができます。
ところで、$\frac{ \vec w^{\top} S_B \vec w }{ \vec w^{\top} S_w \vec w }$は$\vec w$についてスケール不変であるため、分母$\vec w^{\top} S_w \vec w=1$とした下で考えても一般性を失いません。
よって以下では
$$\begin{aligned} \mathrm{maximize} ~~ \vec w^{\top} S_B \vec w ~~~~~ s.t. ~~ \vec w^{\top} S_w \vec w = 1 \end{aligned}$$という最大化問題を解いていきます。
ラグランジュの未定乗数法を用いて解きます。
ラグランジュ関数$L(\vec w, \lambda)$を
$$\begin{aligned} L(\vec w, \lambda) = \vec w^{\top} S_B \vec w-\lambda (\vec w^{\top} S_w \vec w-1) \end{aligned}$$とおくと、
$$\begin{aligned} \frac{\partial L(\vec w, \lambda)}{\partial \vec w} &= 2 S_B \vec w-2 \lambda S_w \vec w = 0 \\[10px] \Rightarrow (S_w^{-1} S_B) \vec w &= \lambda \vec w ~~~~~ \mathrm{(C)} \\ &{\scriptsize(この式は固有値問題に相当)} \\[10px] \frac{\partial L(\vec w, \lambda)}{\partial \lambda} &= -(\vec w^{\top} S_w \vec w-1) = 0 \\[10px] \Rightarrow \vec w^{\top} S_w \vec w &= 1 ~~~~~ \mathrm{(D)} \\ &{\scriptsize(この式は制約条件に相当)} \end{aligned}$$となり、$\mathrm{(C)}$の固有ベクトルを求める問題に帰着されます。
(その固有ベクトルを定数倍してあげれば$\mathrm{(D)}$を満たす様にすることができるため、実質的には$\mathrm{(C)}$のみ考えればよいわけです。より詳細には補足2を参照ください。)
固有値$\lambda$については、$\mathrm{(C)}$に左から$\vec w^{\top} S_w$を作用させてみると、
$$\begin{aligned} \vec w^{\top} S_w (S_w^{-1} S_B) \vec w &= \vec w^{\top} S_w \lambda \vec w \\[10px] \Rightarrow \lambda = \frac{\vec w^{\top} S_B \vec w}{\vec w^{\top} S_w \vec w} &= \vec w^{\top} S_B \vec w \\ &{\scriptsize(\vec w^{\top} S_w \vec w=1より)} \end{aligned}$$となることから『$\lambda$は最大化させたい$\vec w^{\top} S_B \vec w$(射影後の群間変動)そのものである』ということがわかります。
ここで、$S_w$は正則行列であるため、
$$\begin{aligned} \rank (S_w^{-1} S_B) = \rank(S_B) = 1 \end{aligned}$$より(補足3)、$\mathrm{(C)}$の固有値は1つであることがわかり、これに対応する固有ベクトルの1つ$\vec w^{*}$は、
$$\begin{aligned} \vec w^{*} = S_w^{-1} (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)}) ~~~~~ \mathrm{(E)} \end{aligned}$$となります(補足1)。
この固有ベクトルが射影軸となるわけです。
補足1.
天下り的に$\vec w^{*}$を紹介しましたが、これが$\mathrm{(C)}$を成立することを確認しておきましょう。
$\mathrm{(C)}$の左辺で$\vec w = \vec w^{*}$としたものは、
$$\begin{aligned} (S_w^{-1} S_B) \vec w^{*} &= S_w^{-1} (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)}) \underbrace{(\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)})^{\top} S_w^{-1} (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)})}_{\bullet} \\ &{\scriptsize((B),(E)より)} \\[10px] &= \underbrace{(\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)})^{\top} S_w^{-1} (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)})}_{\bullet} \underbrace{S_w^{-1} (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)})}_{\vec w^{*}} \\ &{\scriptsize(\bulletはスカラーなので前に出すことができる)} \end{aligned}$$となりますが、$\bullet = \lambda$とすれば$\mathrm{(C)}$が成立することがわかります。
先述した通り、$\rank (S_w^{-1} S_B) = 1$、より$\mathrm{(C)}$の固有値問題に対応する$\lambda$は、
$$\begin{aligned} \lambda &= (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)})^{\top} S_w^{-1} (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)}) \end{aligned}$$の1つのみです。
補足2.
$\mathrm{(C)}$の固有値として紹介した$\vec w = \vec w^{*} (=S_w^{-1} (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)}))$はこのままでは$\mathrm{(D)}$を成立させませんが、適当に定数倍することで$\mathrm{(D)}$を成立させます。
ただし、$\mathrm{(D)}$を成立させる様に定数倍すると形が汚くなること、$\mathrm{(D)}$は$\vec w$をスケーリングするための条件であり射影軸を求めるという観点からは$\vec w$をスケーリングする必要はないこと、を考慮するとこのままの形で十分です。
補足3.
$S_w$は正則行列、つまり逆行列が存在する行列です。
また、一般的に行列$A,B$に対して、
$$\begin{aligned} \rank (AB) \leqq \rank (A) \\ \rank (AB) \leqq \rank (B) \end{aligned}$$が成立します。
よって、
$$\begin{aligned} \rank(S_B) = \rank(S_w S_w^{-1} S_B) \leqq \rank(S_w^{-1} S_B) \leqq \rank(S_B) \\[10px] \Rightarrow \rank (S_w^{-1} S_B) = \rank(S_B) \end{aligned}$$となります。
1-3. 新たなサンプルのクラスの判別
新たなサンプルの特徴量データ$\vec x_{new}$を元にこのサンプルがどのクラスに判別されるかを決定します。
決定の仕方としては、新たなサンプルの特徴量データ$\vec x_{new}$をを(既存のサンプルから定められた)射影軸に射影し、それと各クラスの射影軸上の平均とを比較して、最も近くのクラスに判別する、という流れになります。
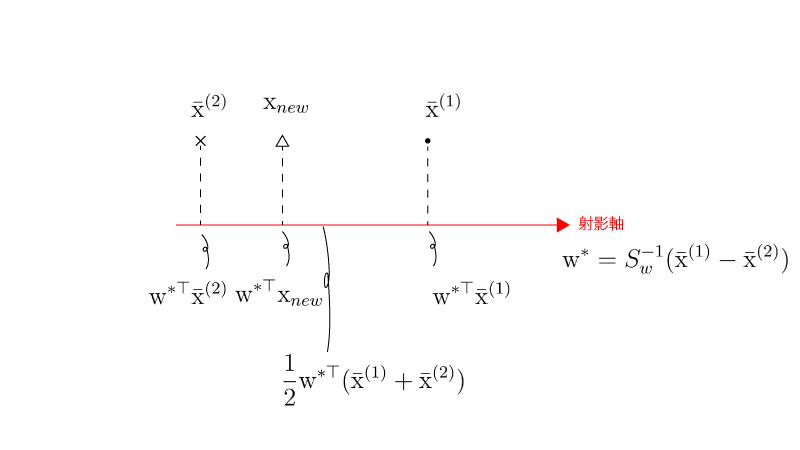
具体的には、$\vec w^{* \top} \vec x_{new}$が$\vec w^{* \top} \bar{\vec x}^{(1)}$と$\vec w^{* \top} \bar{\vec x}^{(2)}$のどちらに近いのかを以て決定しますが、これは$\vec w^{* \top} \vec x_{new}$と($\vec w^{* \top} \bar{\vec x}^{(1)}$と$\vec w^{* \top} \bar{\vec x}^{(2)}$との中点)との位置関係から決定するとも考えられます。
$\vec w^{* \top} \bar{\vec x}^{(1)} \gt \vec w^{* \top} \bar{\vec x}^{(2)}$であることを考慮すると(補足4)、
$$\begin{aligned} f(\vec x_{new}) &= \vec w^{* \top} \vec x_{new}-\frac{1}{2} (\vec w^{* \top} \bar{\vec x}^{(1)} + \vec w^{* \top} \bar{\vec x}^{(2)}) \\[10px] &= \vec w^{* \top} \vec x_{new}-\frac{1}{2} (S_w^{-1} (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)}))^{\top} (\bar{\vec x}^{(1)} + \bar{\vec x}^{(2)}) \\[10px] &= \vec w^{* \top} \vec x_{new}-\frac{1}{2} (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)})^{\top} (S_w^{-1})^{\top} (\bar{\vec x}^{(1)}+\bar{\vec x}^{(2)}) \\[10px] &= \vec w^{* \top} \vec x_{new}-\frac{1}{2} (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)})^{\top} S_w^{-1} (\bar{\vec x}^{(1)}+\bar{\vec x}^{(2)}) ~~~~~ \mathrm{(F)} \\ &{\scriptsize(S_w^{-1}は対称行列であるため(S_w^{-1})^{\top}=S_w^{-1})} \end{aligned}$$を用いて、
・$f(\vec x_{new}) \gt 0 \Rightarrow \vec x_{new}$をクラス1に判別
・$f(\vec x_{new}) \lt 0 \Rightarrow \vec x_{new}$をクラス2に判別
となります。
$f(\vec x_{new})$は『線形判別関数』と一般に呼ばれます。線形判別関数$f(\vec x_{new})$を用いた判別のイメージは下記の通りとなります。
($f(\vec x) \gt 0$の場合)
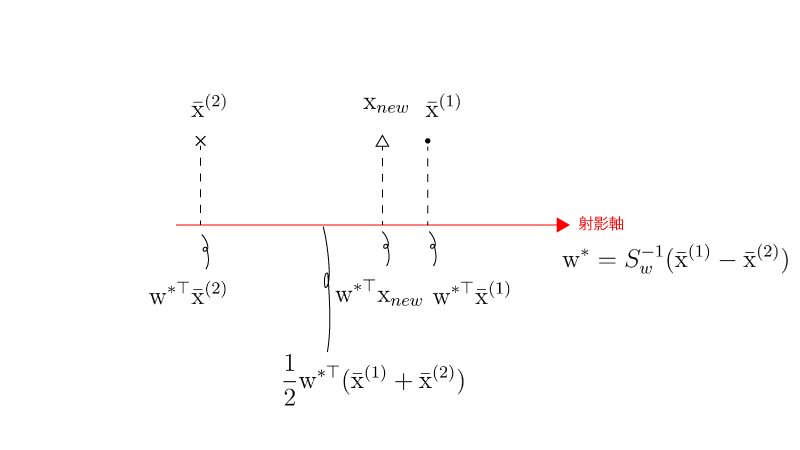
($f(\vec x) \lt 0$の場合)
補足4.
その定義の形から$S_w, S_w^{-1}$は正定値行列であるため、
$$\begin{aligned} \underbrace{(\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)})^{\top} S_w^{-1}}_{\vec w^{* \top}} (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)}) &\gt 0 \\ {\scriptsize(\vec w^{*} = S_w^{-1} (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)})とS_w^{-1 \top} = S_w^{-1}より)} \\[10px] \Rightarrow \vec w^{* \top} \bar{\vec x}^{(1)}-\vec w^{* \top} \bar{\vec x}^{(2)} &\gt 0 \end{aligned}$$
2. (Fisherの)(線形)判別分析、3クラス以上
$a(\geqq 3)$クラスについての特徴量データを$\vec x_i^{(k)} ~~ \small{(k=1,\cdots,a;i=1,\cdots,n_k)}$とします。
この時、郡内変動行列$S_w$、群間変動行列$S_B$は、
$$\begin{aligned} S_w &= \sum_{k=1}^{a} \sum_{i=1}^{n_k} ( \vec x_i^{(k)}-\bar{\vec x}^{(k)} ) ( \vec x_i^{(k)}-\bar{\vec x}^{(k)} )^{\top} ~~~~~ \mathrm{(A)’} \\[10px] S_B &= \sum_{k=1}^{a} n_k \cdot (\bar{\vec x}^{(k)}-\bar{\vec x}) (\bar{\vec x}^{(k)}-\bar{\vec x})^{\top} ~~~~~ \mathrm{(B)’} \end{aligned}$$と定義されます。
$\mathrm{(A)’},\mathrm{(B)’}$はそれぞれ$\mathrm{(A)},\mathrm{(B)}$とやや形が異なりますね。
ぱっと見形が異なりますがは$\mathrm{(A)},\mathrm{(B)}$はそれぞれ$\mathrm{(A)’},\mathrm{(B)’}$の形で書き直すことができます。
つまり、$\mathrm{(A)’},\mathrm{(B)’}$はそれぞれ$\mathrm{(A)},\mathrm{(B)}$を一般化したものになっているわけです。
以下は2クラスの時と同様に、
$$\begin{aligned} \text{maximize}~ \frac{ \vec w^{\top} S_B \vec w }{ \vec w^{\top} S_w \vec w } ~~~~~ s.t. ~~ \vec w^{\top} S_w \vec w = 1 \end{aligned}$$という最大化問題を考えることになり、即ち、
$$\begin{aligned} (S_w^{-1} S_B) \vec w &= \lambda \vec w ~~~~~ \mathrm{(C)’} \end{aligned}$$という固有ベクトルを求める問題に帰着されます。
ここで
$$\begin{aligned} \rank (S_w^{-1} S_B) = \rank(S_B) = a-1 \end{aligned}$$より、$\mathrm{(C)}$の固有値は$(a-1) (\geqq 2)$個であることがわかります。
『1. (Fisherの)(線形)判別分析、2クラス』>『1-2. 射影軸の決定(計算)』では、$\mathrm{(C)}$の固有値は1つであり(その固有値に対応する固有ベクトルを天下り的に紹介しました)、紹介した固有ベクトルが射影軸となりました。
3クラス以上を扱う今回は、$\mathrm{(C’)}$の固有値は複数であり、射影軸は下記の通り決定されます。(証明は割愛)
・射影軸が1つの場合: $\mathrm{(C’)}$の解のうち1番大きな固有値に対応する固有ベクトルが、その射影軸となります。
・射影軸が2つの場合: $\mathrm{(C’)}$の解のうち上から大きな2つの固有値に対応する固有ベクトルが、その射影軸となります。
・射影軸が3つの場合: $\mathrm{(C’)}$の解のうち上から大きな3つの固有値に対応する固有ベクトルが、その射影軸となります。
・(以下略)
射影軸をいくつに設定すべきかは対応する問題によりけりです。
シンプルに可視化したいということであれば射影軸を2ないし3とすることで、2次元ないし3次元のプロットに落とし込むことができます。
例1.
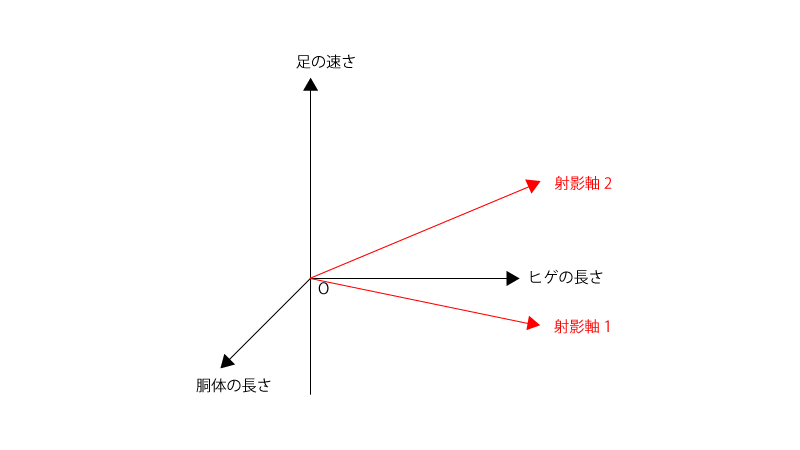
既存のサンプル(10匹の猫、10匹の犬、10匹のウサギ)についてある特徴量(ヒゲの長さ、胴体の長さ、足の速さ)のデータがあるとする。
この時、3(クラスの数)-1=2より、射影軸は2つまでとることができる。
新たなサンプルがどのクラスに属するかを判定するにあたり、射影軸2つを用いて判定する場合、$\mathrm{(C’)}$の解のうち上から大きな2つの固有値に対応する固有ベクトルをその射影軸として定める。
(それぞれのサンプルのプロットは省略)
その後各クラスの平均と新たなサンプルを射影軸上にプロットしてみて下記の様になったとすれば、
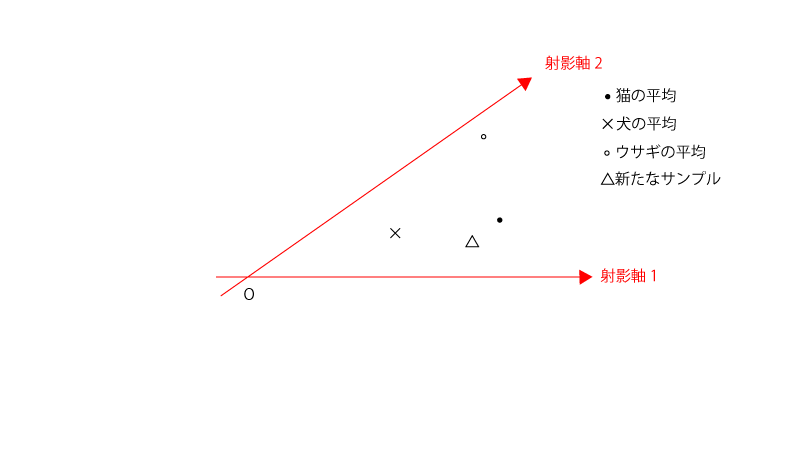
新たなサンプルのクラスは猫と判定される。
新たなサンプルがどのクラスに属するかを判定するにあたり、射影軸1つを用いて判定する場合、$\mathrm{(C’)}$の解のうち上から大きな1つの固有値に対応する固有ベクトルをその射影軸として定める。
その後プロットしてみて下記の様になったとすれば、
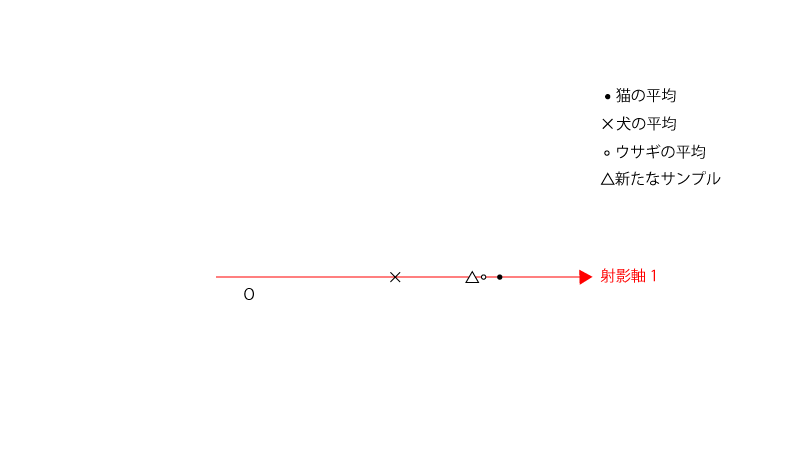
新たなサンプルはウサギと判定される。
3. おまけ
3-1. マハラノビスの距離
『1. (Fisherの)(線形)判別分析、2クラス』>『1-3. 新たなサンプルのクラスの判別』、では$f(\vec x_{new})$を用いて新たなサンプルのクラスを判別しました。
$f(\vec x_{new})$ではなく、『マハラノビスの距離』という「データの多次元構造を考慮した距離」を以て、新たなサンプルのクラスを判別することもできます。
マハラノビスの距離$D$は一般に、
$$\begin{aligned} D(\vec x, \vec y) &= \sqrt{(\vec x-\vec y)^{\top} S^{-1} (\vec x-\vec y)} \\ &{\scriptsize(Sは集団の共分散行列)} \end{aligned}$$と書くことができます。
クラス1とクラス2が同じ分散をもつとすると、その共分散行列は$\frac{1}{n_1 + n_2} S_w$で推定されます。
よって、『$\vec x_{new}$と$\bar{\vec x}^{(1)}$とのマハラノビスの距離の2乗$D^2 (\vec x_1, \vec x_{new})$』、『$\vec x_{new}$と$\bar{\vec x}^{(2)}$とのマハラノビスの距離の2乗$D^2 (\vec x_2, \vec x_{new})$』は下記の様に書くことができます。
$$\begin{aligned} D^2 (\vec x_1, \vec x_{new}) &= (\vec x_{new}-\bar{\vec x}^{(1)})^{\top} (n_1 + n_2) S_w^{-1} (\vec x_{new}-\bar{\vec x}^{(1)}) \\[10px] D^2 (\vec x_2, \vec x_{new}) &= (\vec x_{new}-\bar{\vec x}^{(2)})^{\top} (n_1 + n_2) S_w^{-1} (\vec x_{new}-\bar{\vec x}^{(2)}) \end{aligned}$$
この時、
・$D^2 (\vec x_1, \vec x_{new}) \lt D^2 (\vec x_2, \vec x_{new}) \Rightarrow \vec x_{new}$をクラス1に判別
・$D^2 (\vec x_1, \vec x_{new}) \gt D^2 (\vec x_2, \vec x_{new}) \Rightarrow \vec x_{new}$をクラス2に判別
という形で判別されます。
以下、マハラノビスの距離を用いた場合の判別と$f(\vec x_{new})$を用いた場合の判別の関係性を確認しておきます。
$$\begin{aligned} 2 f(\vec x_{new}) &= 2 \vec w^{* \top} \vec x_{new}-(\vec w^{* \top} \bar{\vec x}^{(1)} + \vec w^{* \top} \bar{\vec x}^{(2)}) \\[10px] &= \vec w^{* \top} (\vec x_{new}-\bar{\vec x}^{(1)}) + \vec w^{* \top} (\vec x_{new}-\bar{\vec x}^{(2)}) \\[10px] &= (S_w^{-1} (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)}))^{\top} (\vec x_{new}-\bar{\vec x}^{(1)}) \\ &+ (S_w^{-1} (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)}))^{\top} (\vec x_{new}-\bar{\vec x}^{(2)}) \\[10px] &= (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)})^{\top} (S_w^{-1})^{\top} (\vec x_{new}-\bar{\vec x}^{(1)}) \\ &+ (\bar{\vec x}^{(1)}-\bar{\vec x}^{(2)})^{\top} (S_w^{-1})^{\top} (\vec x_{new}-\bar{\vec x}^{(2)}) \\[10px] &= \{ -(\vec x_{new}-\bar{\vec x}^{(1)}) + (\vec x_{new}-\bar{\vec x}^{(2)}) \}^{\top} S_w^{-1} (\vec x_{new}-\bar{\vec x}^{(1)}) \\ &+ \{ -(\vec x_{new}-\bar{\vec x}^{(1)}) + (\vec x_{new}-\bar{\vec x}^{(2)}) \}^{\top} S_w^{-1} (\vec x_{new}-\bar{\vec x}^{(2)}) \\ &{\scriptsize(S_w^{-1}は対称行列であるため(S_w^{-1})^{\top}=S_w^{-1})} \\[10px] &= -\frac{1}{n_1 + n_2} D^2 (\vec x_1, \vec x_{new}) + \frac{1}{n_1 + n_2} D^2 (\vec x_2, \vec x_{new}) \end{aligned}$$
よって、
・$f(\vec x_{new}) \gt 0 \Rightarrow D^2 (\vec x_1, \vec x_{new}) \lt D^2 (\vec x_2, \vec x_{new}) \Rightarrow \vec x_{new}$をクラス1に判別
・$f(\vec x_{new}) \lt 0 \Rightarrow D^2 (\vec x_1, \vec x_{new}) \gt D^2 (\vec x_2, \vec x_{new}) \Rightarrow \vec x_{new}$をクラス2に判別
となり、マハラノビスの距離を用いた場合の判別と$f(\vec x_{new})$を用いた場合の判別は一致することがわかります。
3-2. 2次判別分析
これまでは1次(線形)判別分析を扱ってきましたが、ここでは2次判別分析を扱います。
違いは以下の様になります。
・1次(線形)判別分析:各クラスにおける郡内変動行列は同じ
・2次判別分析:各クラスにおける郡内変動行列は異なる
したがって、2次判別分析におけるマハラノビスの距離は以下の様に異なる郡内変動行列を用いて定義されます。
$$\begin{aligned} D^2 (\vec x_1, \vec x_{new}) &= (\vec x_{new}-\bar{\vec x}^{(1)})^{\top} (n_1 + n_2) S_{w1}^{-1} (\vec x_{new}-\bar{\vec x}^{(1)}) \\[10px] D^2 (\vec x_2, \vec x_{new}) &= (\vec x_{new}-\bar{\vec x}^{(2)})^{\top} (n_1 + n_2) S_{w2}^{-1} (\vec x_{new}-\bar{\vec x}^{(2)}) \end{aligned}$$
判別は1次判別分析の場合と同じく、
・$D^2 (\vec x_1, \vec x_{new}) \lt D^2 (\vec x_2, \vec x_{new}) \Rightarrow \vec x_{new}$をクラス1に判別
・$D^2 (\vec x_1, \vec x_{new}) \gt D^2 (\vec x_2, \vec x_{new}) \Rightarrow \vec x_{new}$をクラス2に判別
となります。
1次(線形)判別分析と2次判別分析とどちらの方がよいのでしょうか?
一概にどちらの方が良いとは言えません。
2次判別分析の方が柔軟な判別が可能ですが、各クラスのサンプルサイズが小さい場合にはその判別が不安定になりやすいです。
まとめ.
- 判別分析とは、新たなサンプルの特徴量を用いて、それが所属するクラスを判別する方法である。
- 判別分析の具体的な流れは以下の通りである。
step 1. 既存のサンプルについての特徴量から射影軸を決定する
step 2. 新たなサンプルについての特徴量をその射影軸に射影する
step 3. 2で射影されたものと、各クラスの射影軸上の平均とを比較して、最も近くのクラスに判別する






