$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}} \\ \gdef \indep {\mathop{\perp\!\!\!\!\perp}} \\ \gdef \tr {\mathrm{tr}}$
ここからは生存時間解析の検定ですね。
はい。ここでは生存時間曲線として最も有名な『カプランマイヤー曲線』と、その元となる『カプランマイヤー推定量』を扱います。その後、2群の生存関数$S(t)$についての検定として『ログランク検定』を紹介します。
1. カプランマイヤー推定量とカプランマイヤー曲線
カプランマイヤー推定量は生存関数$S(t)$の推定量です。
さて、$n$人の患者さんを対象とした臨床研究において、時点$t_i (i=1, \ldots, h)$でそれぞれ$d_i$回ずつのイベントが発生したとします。右側打ち切りが発生しうると想定して、時点$t_i$の直前までフォローされていた患者さんを$n_i$人とします。(この$n_i$人を、イベントが発生しうる候補者の数ということで、”number at risk“と呼びます)
この時、カプランマイヤー推定量$\hat{S}(t)$は、
$$\begin{aligned} \hat{S}(t) = \begin{cases} 1 ~~~~~ \small{((0 \leqq) t \lt t_1)} \\ \prod_{i; t_i \leqq t} (1-\dfrac{d_i}{n_i}) ~~~~~ \small{(t \geqq t_1)} ~~~~~ \mathrm{(A)} \end{cases} \end{aligned}$$となります。
また、横軸に時点$t$を、縦軸にカプランマイヤー推定量$\hat{S}(t)$をプロットしたものをカプランマイヤー曲線と呼びます。 なお、右側打ち切りが生じた場合には『+』のように縦線を加えるのが通常です。
$\mathrm{(A)}$については『各時点における生存者にイベントが発生する確率、を掛け合わせたもの』となります。イメージしにくい場合には次の例を参照してください。
例1.
ある慢性疾患の10人の患者さんを対象にした臨床試験で、イベントを『死亡』として12ヶ月間フォローすることとなった。この時、イベントまたは右側打ち切りが以下の時点で確認された。(ただし、「+」付きはイベント発生ではなく右側打ち切りが生じたことを表す)
3, 5, 6, 6, 7+, 9+, 10 (単位:ヶ月)
この時、カプランマイヤー推定量$\hat{S}(t)$を求めた上で、カプランマイヤー曲線を描いてみる。
・$0 \leqq t \lt 3$:イベントは発生してないので、$\hat{S}(t)=1$、は明らかである。
・$3 \leqq t \lt 5$:$t=3$で1人にイベントが発生したので、$\hat{S}(t)=1 \cdot (1-\frac{1}{10})$、となる。ここで、”$1-\frac{1}{10}$”の”$\frac{1}{10}$”は『$t=3$の直前で10人フォローされていたが$t=3$で1人にイベントが発生したこと』から由来する。
同様にすると以下の様になる。
$$\begin{aligned} \hat{S}(t) = \begin{cases} 1 \cdot (1-\frac{1}{10}) \cdot (1-\frac{1}{9}) ~~~~~ \small{(5 \leqq t \lt 6)} \\ 1 \cdot (1-\frac{1}{10}) \cdot (1-\frac{1}{9}) \cdot (1-\frac{2}{8}) ~~~~~ \small{(6 \leqq t \lt 10)} \\ 1 \cdot (1-\frac{1}{10}) \cdot (1-\frac{1}{9}) \cdot (1-\frac{2}{8}) \cdot (1-\frac{1}{4}) ~~~~~ \small{(10 \leqq t \lt 12)} \end{cases} \end{aligned}$$
従って以上を整理すると以下の様になる。
$$\begin{aligned} \hat{S}(t) &= \begin{cases} 1 ~~~~~ \small{(0 \leqq t \lt 3)} \\ \frac{9}{10} ~~~~~ \small{(3 \leqq t \lt 5)} \\ \frac{8}{10} ~~~~~ \small{(5 \leqq t \lt 6)} \\ \frac{6}{10} ~~~~~ \small{(6 \leqq t \lt 10)} \\ \frac{9}{20} ~~~~~ \small{(10 \leqq t \lt 12)} \end{cases} \end{aligned}$$
よって、カプランマイヤー曲線は以下の様になる。
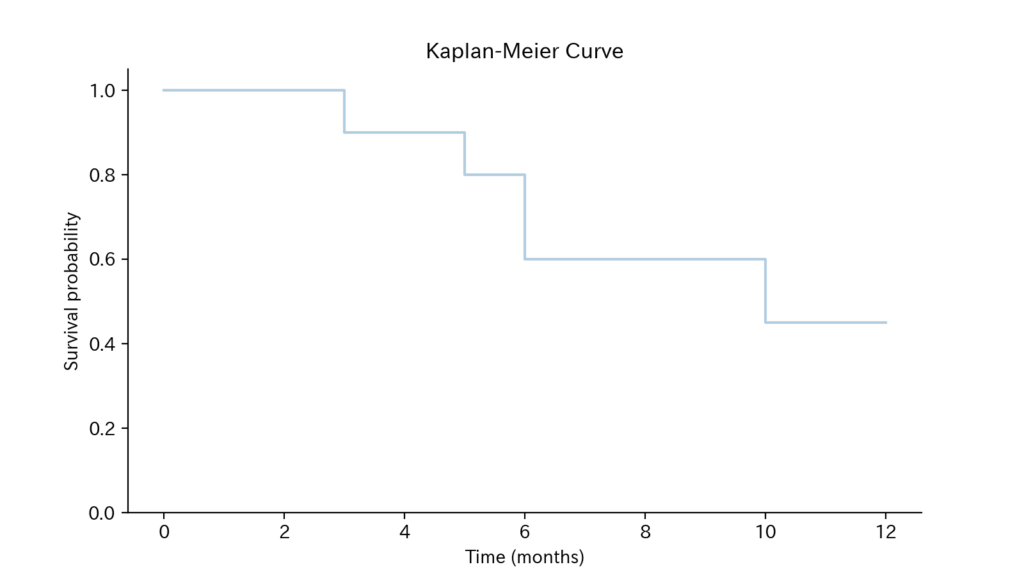
(補足)
カプランマイヤー推定量$\prod_{i; t_i \leqq t} (1-\dfrac{d_i}{n_i}) ~~ \small{(t \geqq t_1)}$については、この様な具体例を通じて考えてみると自然な推定量だと腑に落ちますね。
なお、一気に$S(t)$を考えると混乱しそうであれば下記の様に表を書いてみるのもよいと思います。
| $t$ | 0 | 3 | 5 | 6 | 7 | 9 | 10 |
| $t$直前のnumber at risk | 10 | 10 | 9 | 8 | 6 | 5 | 4 |
| $t$におけるイベント発生数 | 0 | 1 | 1 | 2 | 0 | 0 | 1 |
表を書いてみるとわかりやすいですね。
2. ログランク検定
ログランク検定は2つの生存曲線(生存関数$S(t)$)に差があるかの検定に用いられます。
グループ1, 2の生存関数をそれぞれ$S_1(t), S_2(t)$とする時、ログランク検定の帰無仮説$H_0$、対立仮説$H_1$はそれぞれ以下の通りです。
$$\begin{aligned} \begin{cases} {\small 帰無仮説} H_0: S_1(t) = S_2(t) ~~~~~ (\forall t) \\ {\small 帰無仮説} H_1: H_0 {\small が不成立} \end{cases} \end{aligned}$$
いずれかのグループでイベントが発生した時点を$t_j$とし、時点$t_j$における各グループのnumber at riskをそれぞれ$n_{1, j}$人、$n_{2, j}$人、時点$t_j$における各グループのイベント発生数をそれぞれ$d_{1,j}$、$d_{2,j}$とします。 (ただし、$n_j = n_{1,j} + n_{2,j}, d_j = d_{1,j} + d_{2,j}$とします)
帰無仮説$H_0$の下で$d_{i,j} ~~ {\small (i=1,2)}$は、$n_j, n_{i,j}, d_j$を条件付けた上で、超幾何分布$\HG(n_j, n_{i,j}, d_j)$に従うため、
$$\begin{aligned} E[d_{i,j}] &= d_j (\frac{n_{i,j}}{n_j}) \\ V[d_{i,j}] &= d_j (\frac{n_{i,j}}{n_j}) (1-\frac{n_{i,j}}{n_j}) \cdot \frac{n_j-n_{i,j}}{n_j-1} \end{aligned}$$となります。(参照:<離散分布>>「超幾何分布」)
そして、ログランク統計量$Z$について、
$$\begin{aligned} Z = \frac{\sum_j (d_{\textcolor{red}{1},j}-E[d_{\textcolor{red}{1},j}])} { \sqrt{ \sum_j V[d_{\textcolor{red}{1},j}]} } \overset{\displaystyle {d}}\longrightarrow \N(0,1) \end{aligned}$$
が成立すること、または$Z^2$について、
$$\begin{aligned} Z^2 = \frac{(\sum_j (d_{\textcolor{red}{1},j}-E[d_{\textcolor{red}{1},j}]))^2} { \sum_j V[d_{\textcolor{red}{1},j}] } \overset{\displaystyle {d}}\longrightarrow \chi^2 (1) \end{aligned}$$が成立することを用いて検定を行います。
(ただし、赤文字部分は”$2$”でも構いません)
この$Z$または$Z^2$は観測データから計算され、有意水準を$\alpha$とすると、
⚫︎$|Z| \leqq Z_{\textcolor{red}{\frac{\alpha}{2}}} \Rightarrow {\small H_0を選択}$
⚫︎$|Z| \gt Z_{\textcolor{red}{\frac{\alpha}{2}}} \Rightarrow {\small H_1を選択}$
または、
⚫︎$Z^2 \leqq \chi^2_{\textcolor{red}{\alpha}} (1) \Rightarrow {\small H_0を選択}$
⚫︎$Z^2 \gt \chi^2_{\textcolor{red}{\alpha}} (1) \Rightarrow {\small H_1を選択}$
という判定がなされます。
(ただし$Z_{\frac{\alpha}{2}}, \chi^2_{\alpha} (1)$をそれぞれ$\N(0,1)$の上側$\frac{\alpha}{2}$点、$\chi^2 (1)$の上側$\alpha$点とします)
ログランク検定の導出を手計算ですることはないと思いますが、ログランク統計量を導出するにあたっては各時点$t_j$において、$E[d_{1,j}], V[d_{1,j}]$(または$E[d_{2,j}], V[d_{2,j}]$)を用いた計算を逐一する必要があることを認識しておいてください。
まとめ.
- カプランマイヤー推定量は生存関数$S(t)$の推定量であり、それを図示したものがカプランマイヤー曲線である。
- ログランク検定は2つの生存曲線(生存関数)に差があるかの検定に使われ、ログランク統計量の導出にはイベントが発生した各時点での計算が必要である。






