$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}}$
今回は「カルベック・ライブラー情報量」ですか。
『情報量』と言えば、「フィッシャー情報量」を以前勉強しましたね。
実はその$2$つは類似した概念なのです!
。。。どういうことでしょうか?
「カルバック・ライブラー情報量」とは分布間の『キョリ*』なのです。
一方のフィッシャー情報量は(分布パラメータの)推定量の推定精度の指標でしたよね。
そうですね。
実はフィッシャー情報量とは分布パラメータが近い分布間の『キョリ』に影響する因子なのです。フィッシャー情報量が小さいとこの『キョリ』が小さくなり、推定精度が高い、という判定がなされるのです。
まとめると、
- カルバック・ライブラー情報量:任意の分布間の『キョリ*』
- フィッシャー情報量:分布パラメータが近い分布間の『キョリ*』に影響する因子
となりますでしょうか?
その通りです。
*:ここで言う『キョリ』とはいわゆる「距離」ではありません。
点A,Bに対して、
(AからBをみた距離)=(BからAをみた距離)、ですが、
(AからBをみた『キョリ』)=(BからAをみた『キョリ』)、は必ずしも成立しません。
1. カルバック・ライブラー情報量
(定義)
分布P, Qの確率密度関数を$p(x), q(x)$とした時、
カルバック・ライブラー情報量$KL(P||Q)$は、
$$\begin{aligned} KL(P||Q) = \int_{-\infty}^{\infty} p(x) \cdot \log(\frac{p(x)}{q(x)}) dx \end{aligned}$$と定義されます。
ただし、以下の通りとします。
- $p(x)=0$の時は($q(x)=0$の時を含め)$\int$内は$0$
- $p(x) \neq 0, q(x) = 0$の時は$\int$内は$\infty$
- 確率関数の場合には、上式の$\int$を$\sum$に置換する
(注意:本記事では以下確率密度関数の場合のみ扱う)
上式で$p(x), q(x)$に対称性がないことから、$KL(P||Q)=KL(Q||P)$、は一般には成立しません。
それでは以下の例を通じてイメージを確立してください。
例題1.
分布P:$\N(0,1)$、分布Q:$\N(\mu, 1)$、とした時、カルバック・ライブラー情報量$KL(P||Q)$を求めそれを図示せよ。
解答.
分布P, Qの確率密度関数をそれぞれ$p(x), q(x)$とすると、
$$\begin{aligned} p(x) &= \frac{1}{\sqrt{2 \pi}} \exp(-\frac{x^2}{2}) \\[10px] q(x) &= \frac{1}{\sqrt{2 \pi }} \exp(-\frac{(x-\mu)^2}{2}) \end{aligned}$$である。
よって$KL(P||Q)$については、
$$\begin{aligned} KL(P||Q) &= \int_{-\infty}^{\infty} p(x) \cdot \log(\frac{p(x)}{q(x)}) dx \\[10px] &= \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}} \exp(-\frac{x^2}{2}) \cdot \log (\frac{\frac{1}{\sqrt{2 \pi}} \exp(-\frac{x^2}{2})}{\frac{1}{\sqrt{2 \pi }} \exp(-\frac{(x-\mu)^2}{2})}) dx \\[10px] &= \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \exp(-\frac{x^2}{2}) \cdot \log (\exp[\frac{-2\mu x + \mu^2}{2}]) dx \\[10px] &= \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \exp(-\frac{x^2}{2}) \cdot (-\mu x + \frac{1}{2} \mu^2) dx \\[10px] &= \frac{1}{\sqrt{2 \pi}} \{ (-\mu) \underbrace{\int_{-\infty}^{\infty} \exp(-\frac{x^2}{2}) \cdot x dx}_{=0 ~~ (\int内は奇関数)} + (\frac{\mu^2}{2}) \underbrace{\int_{-\infty}^{\infty} \exp(-\frac{x^2}{2}) dx}_{=\sqrt{2\pi} ~~ (ガウス積分)} \} \\[10px] &= \frac{\mu^2}{2} \end{aligned}$$となる。
また$KL(P||Q)$は図示すると以下の様になる。
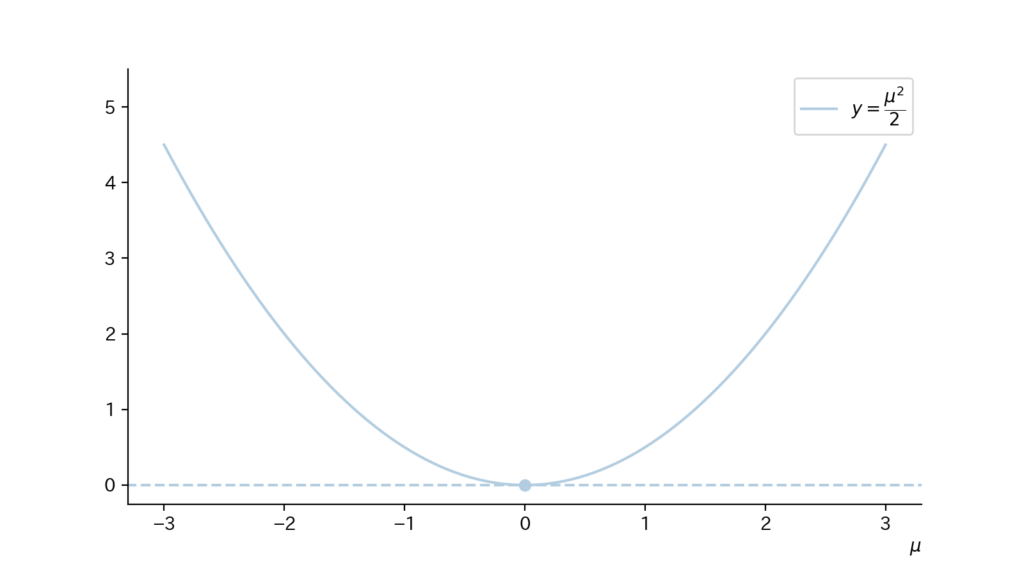
$KL(P||Q)$は$\mu$の値に応じて$2$次関数的に変化していくのですね。
また$\mu=0$の時(即ち、$P=Q$の時)は、$KL(P||Q)(=KL(P||P))=0$、となってますね。
例題2.
分布P:$\N(0,1)$、分布Q:$\N(0, \sigma^2)~~ \small{(\sigma \gt 0)}$、とした時、カルバック・ライブラー情報量$KL(P||Q)$を求めそれを図示せよ。
解答.
分布P, Qの確率密度関数をそれぞれ$p(x), q(x)$とすると、
$$\begin{aligned} p(x) &= \frac{1}{\sqrt{2 \pi}} \exp(-\frac{x^2}{2}) \\[10px] q(x) &= \frac{1}{\sqrt{2 \pi \sigma^2 }} \exp(-\frac{x^2}{2 \sigma^2}) \end{aligned}$$である。
よって$KL(P||Q)$については、
$$\begin{aligned} KL(P||Q) &= \int_{-\infty}^{\infty} p(x) \cdot \log(\frac{p(x)}{q(x)}) dx \\[10px] &= \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}} \exp(-\frac{x^2}{2}) \cdot \log (\frac{\frac{1}{\sqrt{2 \pi}} \exp(-\frac{x^2}{2})}{\frac{1}{\sqrt{2 \pi \sigma^2 }} \exp(-\frac{x^2}{2 \sigma^2})}) dx \\[10px] &= \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}} \exp(-\frac{x^2}{2}) \cdot \{ (\frac{1}{2 \sigma^2}-\frac{1}{2}) x^2 + \log \sigma \} dx \\[10px] &= \frac{1}{\sqrt{2 \pi}} \left[ (\frac{1}{2 \sigma^2}-\frac{1}{2}) \underbrace{\int_{-\infty}^{\infty} \exp(-\frac{x^2}{2}) \cdot x^2 dx}_{(1)} + (\log \sigma) \underbrace{\int_{-\infty}^{\infty} \exp(-\frac{x^2}{2}) dx}_{=\sqrt{2\pi} ~~ (ガウス積分)} \right] \end{aligned}$$となる。
ここで上式の$\mathrm{(1)}$について、
$$\begin{aligned} \int_{-\infty}^{\infty} \exp(-\frac{x^2}{2}) \cdot x^2 dx &= \int_{-\infty}^{\infty} (-x) [\exp(-\frac{x^2}{2})]^{\prime} dx \\[10px] &= \left[(-x) \exp(-\frac{x^2}{2}) \right]_{-\infty}^{\infty}-\int_{-\infty}^{\infty}(-1) \exp(-\frac{x^2}{2}) dx \\[10px] &= (0-0) + \sqrt{2 \pi} \\ &{\scriptsize (2項目はガウス積分より)} \\[10px] &= \sqrt{2 \pi} \end{aligned}$$となるので、まとめると、
$$\begin{aligned} KL(P||Q) &= \frac{1}{\sqrt{2 \pi}} [(\frac{1}{2 \sigma^2}-\frac{1}{2}) \cdot \sqrt{2 \pi} + (\log \sigma) \cdot \sqrt{2 \pi}] \\[10px] &= \frac{1}{2 \sigma^2}-\frac{1}{2} + \log \sigma \end{aligned}$$
また$KL(P||Q)$は図示すると以下の様になる。
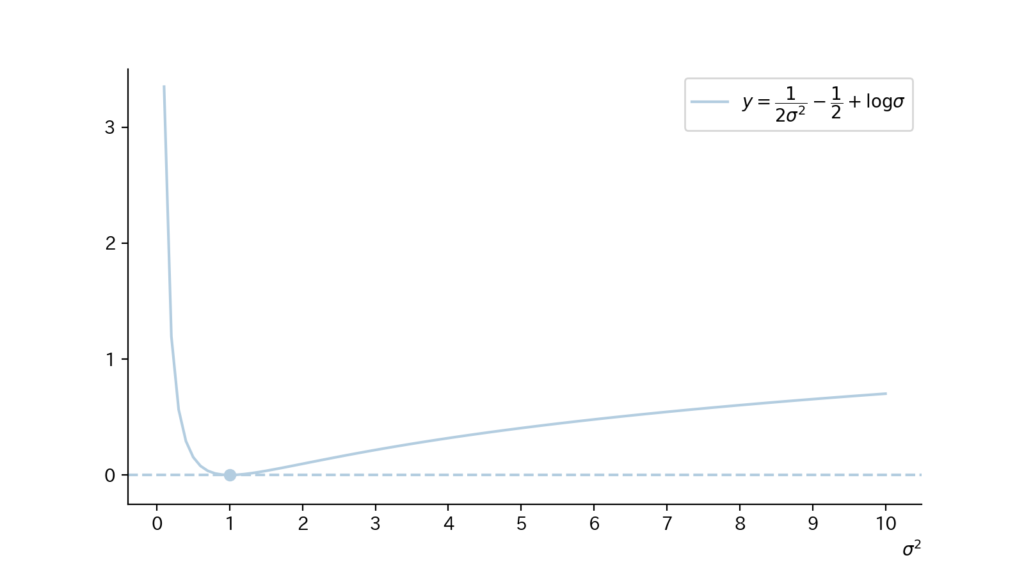
例題2の$KL(P||Q)$は少し複雑な形をしていますね。
また$\sigma^2=1$の時(即ち、$P=Q$の時)は、$KL(P||Q)(=KL(P||P))=0$、となってますね。
2. カルバック・ライブラー情報量について覚えておくべき性質
性質1.
カルバック・ライブラー情報量は非負
性質2.
同一の分布に対してカルバック・ライブラー情報量は$0$
性質3.
カルバック・ライブラー情報量が$0$であれば分布は同一
カルバック・ライブラー情報量は『キョリ』の指標であり、これは「距離」的な概念であることからこれらの性質のイメージは湧くかと思います。
(再掲)性質1.
カルバック・ライブラー情報量は非負
(証明)
分布P, Qの確率密度関数をそれぞれ$p(x), q(x)$とする。
一般に、
$$\begin{aligned} \log x &\leqq x-1 ~~ (\forall x \gt 0) \\ &{\scriptsize (証明は略)} \\ \iff -\log x &\geqq 1-x ~~ (\forall x \gt 0) \end{aligned}$$が成立し、等号成立は$x=1$の時である。
$p(x) \neq 0, q(x) \neq 0$の場合について考えると、上記より、 $$\begin{alignat}{2} &&-\log(\frac{q(x)}{p(x)}) &\geqq 1-\frac{q(x)}{p(x)} \notag \\[10px] &\Rightarrow& -p(x) \cdot \log(\frac{q(x)}{p(x)}) &\geqq p(x)-q(x) \notag \\ &&&{\scriptsize (p(x) (\gt 0)を両辺に乗した)} \notag \\[10px] &\Rightarrow& p(x) \cdot \log(\frac{p(x)}{q(x)}) &\geqq p(x)-q(x) ~~~~~ \mathrm{(A)} \notag \\ &&&{\scriptsize (\log内の分母分子を入れかえた)} \notag \end{alignat}$$となる。
$\mathrm{(A)}$は$p(x) \neq 0, q(x) = 0$の場合についても、
$$\begin{aligned} {\small (上式の左辺)} &= \infty \\[10px] {\small (上式の右辺)} &= p(x) \end{aligned}$$から成立している。
ところで$KL(P||Q)$について考えると、
$$\begin{aligned} KL(P||Q) &= \int_{-\infty}^{\infty} p(x) \cdot \log (\frac{p(x)}{q(x)}) dx \\[10px] &= \underbrace{\int_{x:p(x)=0} p(x) \cdot \log (\frac{p(x)}{q(x)}) dx}_{=0} + \int_{x:p(x) \neq 0} p(x) \cdot \log (\frac{p(x)}{q(x)}) dx \\[10px] &= \int_{x:p(x) \neq 0} p(x) \cdot \log (\frac{p(x)}{q(x)}) dx ~~~~~ \mathrm{(B)} \end{aligned}$$となる。
よって$\mathrm{(A), (B)}$より、
$$\begin{aligned} KL(P||Q) &= \int_{x:p(x) \neq 0} p(x) \cdot \log (\frac{p(x)}{q(x)}) dx \\[10px] &\underbrace{\geqq}_{(1)} \int_{x:p(x) \neq 0} (p(x)-q(x)) dx \\[10px] &= \int_{x:p(x) \neq 0} p(x) dx-\int_{x:p(x) \neq 0} q(x) dx \\[10px] &= \int_{-\infty}^{\infty} p(x) dx-\int_{x:p(x) \neq 0} q(x) dx \\[10px] &\underbrace{\geqq}_{(2)} \int_{-\infty}^{\infty} p(x) dx-\int_{-\infty}^{\infty} q(x) dx \\[10px] &= 1-1 \\ &{\scriptsize (p(x), q(x)はともに確率密度関数なので全区間で積分すると1)} \\[10px] &= 0 \end{aligned}$$
以上より題意は示された。
(再掲)性質2.
同一の分布に対してカルバック・ライブラー情報量は$0$
(証明)
$KL(P||P)$を考えると、
$$\begin{aligned} KL(P||P) &= \int_{-\infty}^{\infty} p(x) \cdot \log(\frac{p(x)}{p(x)}) dx \\[10px] &= \int_{-\infty}^{\infty} p(x) \cdot \underbrace{\log(1)}_{=0} dx \\[10px] &= 0 \end{aligned}$$となるため、題意は示された。
(再掲)性質3.
カルバック・ライブラー情報量が$0$であれば分布は同一
(証明)
$KL(P||Q)=0$なる時、性質1証明の$\mathrm{(1), (2)}$の等号が成立する必要がある。
まず$\mathrm{(1)}$の等号が成立する時、
$$\begin{aligned} \int_{x:p(x) \neq 0} p(x) \cdot \log (\frac{p(x)}{q(x)}) dx = \int_{x:p(x) \neq 0} (p(x)-q(x)) dx \\[10px] \Rightarrow \int_{x:p(x) \neq 0} \left[ p(x) \cdot \log (\frac{p(x)}{q(x)})-( p(x)-q(x) ) \right] dx = 0 \\[10px] \Rightarrow \int_{x:p(x) \neq 0} p(x) \underbrace{\left[ \log (\frac{p(x)}{q(x)})-( 1-\frac{q(x)}{p(x)} ) \right]}_{(\bullet)} dx = 0 \end{aligned}$$と整理できる。
$\mathrm{(\bullet)} \geqq 0$であるから、上式が成立するためには$x:p(x) \neq 0$なる$x$において常に$\mathrm{(\bullet)} = 0$となる必要がある。
つまり、$x:p(x) \neq 0$なる$x$において
$$\begin{aligned} \frac{q(x)}{p(x)} &= 1 \\[10px] \Rightarrow p(x) &= q(x) \end{aligned}$$となる必要がある。
続いて$\mathrm{(2)}$の等号が成立する時、$x:p(x)=0$なる$x$において$q(x)=0$となる必要がある。
まとめると$KL(P||Q)=0$なる時、任意の$x$において$p(x)=q(x)$が成立している。
以上より題意は示された。
3. カルバック・ライブラー情報量とフィッシャー情報量
冒頭の会話で
- カルバック・ライブラー情報量:任意の分布間の『キョリ』
- フィッシャー情報量:分布パラメータが近い分布間の『キョリ』に影響する因子
と紹介しました。
以下これを数式にて説明します。
ただし$P, Q$は同じ分布族に属し、$P$:分布パラメータ$\theta=\theta_0$と固定、$Q$:分布パラメータ$\theta$は任意として、$KL(P||Q)$の代わりに$KL(\theta_0||\theta)$と表します。
また積分区間は$-\infty \sim \infty$ですが、これは省略します。
(本説明の準備)
以下の$\mathrm{(C)-(E)}$が成立します。
(ただし、$I(\theta_0)$はフィッシャー情報量を表します)
$$\begin{aligned} KL(\theta_0||\theta) = \int f(x;\theta_0) \cdot \log f(x;\theta_0) dx-\int f(x;\theta_0) \cdot \log f(x;\theta) dx ~~~~~ \mathrm{(C)} \end{aligned}$$
$$\begin{aligned} \left.\left( \frac{\partial}{\partial \theta} KL(\theta_0||\theta) \right)\right|_{\theta=\theta_0} = 0 ~~~~~ \mathrm{(D)} \end{aligned}$$
$$\begin{aligned} \left.\left( \frac{\partial^2}{\partial \theta^2} KL(\theta_0||\theta) \right)\right|_{\theta=\theta_0} = I(\theta_0) ~~~~~ \mathrm{(E)} \end{aligned}$$
($\mathrm{(C)}$の証明)
$$\begin{aligned} KL(\theta_0||\theta) &= \int f(x;\theta_0) \cdot \log(\frac{f(x;\theta_0)}{f(x;\theta)}) dx \\ &{\scriptsize (定義より)} \\[10px] &= \int f(x;\theta_0) \cdot \log f(x;\theta_0) dx-\int f(x;\theta_0) \cdot \log f(x;\theta) dx \end{aligned}$$
($\mathrm{(D)}$の証明)
$$\begin{aligned} \left.\left( \frac{\partial}{\partial \theta} KL(\theta_0||\theta) \right)\right|_{\theta=\theta_0} &= \left.\left( \frac{\partial}{\partial \theta} \int f(x;\theta_0) \cdot \log f(x;\theta_0) dx-\frac{\partial}{\partial \theta}\int f(x;\theta_0) \cdot \log f(x;\theta) dx \right)\right|_{\theta=\theta_0} \\ &{\scriptsize ((C)より)} \\[10px] &= \left.\left( -\frac{\partial}{\partial \theta}\int f(x;\theta_0) \cdot \log f(x;\theta) dx \right)\right|_{\theta=\theta_0} \\[10px] &= \left.\left( -\int f(x;\theta_0) \cdot \frac{\partial}{\partial \theta} \log f(x;\theta) dx \right)\right|_{\theta=\theta_0} \\ &{\scriptsize (微分と積分の交換が可能とした)} \\[10px] &= \left.\left( -\int f(x;\theta_0) \cdot \frac{\frac{\partial}{\partial \theta} f(x;\theta)}{f(x;\theta)} dx \right)\right|_{\theta=\theta_0} \\[10px] &= -\int f(x;\theta_0) \cdot \frac{\frac{\partial}{\partial \theta} f(x;\theta_0)}{f(x;\theta_0)} dx \\[10px] &= -\int \frac{\partial}{\partial \theta} f(x;\theta_0) dx \\[10px] &= -\frac{\partial}{\partial \theta} \int f(x;\theta_0) dx \\ &{\scriptsize (微分と積分の交換が可能とした)} \\[10px] &= 0 \end{aligned}$$
($\mathrm{(E)}$の証明)
$$\begin{aligned} \left.\left( \frac{\partial^2}{\partial \theta^2} KL(\theta_0||\theta) \right)\right|_{\theta=\theta_0} &= \left.\left( \frac{\partial^2}{\partial \theta^2} \int f(x;\theta_0) \cdot \log f(x;\theta_0) dx-\frac{\partial^2}{\partial \theta^2}\int f(x;\theta_0) \cdot \log f(x;\theta) dx \right)\right|_{\theta=\theta_0} \\ &{\scriptsize ((C)より)} \\[10px] &= \left.\left( -\frac{\partial^2}{\partial \theta^2}\int f(x;\theta_0) \cdot \log f(x;\theta) dx \right)\right|_{\theta=\theta_0} \\[10px] &= \left.\left( -\int f(x;\theta_0) \cdot \frac{\partial^2}{\partial \theta^2} \log f(x;\theta) dx \right)\right|_{\theta=\theta_0} \\ &{\scriptsize (微分と積分の交換が可能とした)} \\[10px] &= \left. E\left[ -\frac{\partial^2}{\partial \theta^2} \log f(X;\theta) \right]\right|_{\theta=\theta_0} \\[10px] &= I(\theta_0) \\ &{\scriptsize (フィッシャー情報量の定義より)} \end{aligned}$$
(本説明)
$KL(\theta_0||\theta)$について$\theta_0$まわりでのTaylor展開して整理すると、
$$\begin{aligned} KL(\theta_0||\theta) &= KL(\theta_0||\theta_0) + \frac{1}{1!} \left.\left( \frac{\partial}{\partial \theta} KL(\theta_0||\theta) \right)\right|_{\theta=\theta_0} \cdot (\theta-\theta_0) + \frac{1}{2!} \left.\left( \frac{\partial^2}{\partial \theta^2} KL(\theta_0||\theta) \right)\right|_{\theta=\theta_0} \cdot (\theta-\theta_0)^2 + \cdots \\[10px] &\fallingdotseq \underbrace{KL(\theta_0||\theta_0)}_{=0 ~~ (性質2より)} + \frac{1}{1!} \underbrace{\left.\left( \frac{\partial}{\partial \theta} KL(\theta_0||\theta) \right)\right|_{\theta=\theta_0}}_{=0 ~~ ((D)より)} \cdot (\theta-\theta_0) + \frac{1}{2!} \underbrace{\left.\left( \frac{\partial^2}{\partial \theta^2} KL(\theta_0||\theta) \right)\right|_{\theta=\theta_0}}_{=I(\theta_0) ~~ ((E)より)} \cdot (\theta-\theta_0)^2 \\[10px] &= \frac{1}{2} I(\theta_0) \cdot (\theta-\theta_0)^2 \end{aligned}$$となります。
カルバック・ライブラー情報量とは任意の分布間の『キョリ』だったので、上式よりフィッシャー情報量が分布パラメータが近い分布間の『キョリ』に影響する因子であることが理解できます。
(本説明の補足)
- カルバック・ライブラー情報量$KL(\theta_0||\theta)$における$\theta$は任意でしたが、上記ではTaylor展開を用いた近似をしたので、
$$\begin{aligned} KL(\theta_0||\theta) \fallingdotseq \frac{1}{2} I(\theta_0) \cdot (\theta-\theta_0)^2 \end{aligned}$$が成立するのは$\theta$が$\theta_0$付近にある時のみです。 - ここまでの流れの補助のために以下Figを考えてみます。
(青の$KL_1(\theta_0 || \theta)$とそれを$\theta_0$まわりで近似した薄青、グレーの$KL_2(\theta_0 || \theta)$とそれを$\theta_0$まわりで近似した薄グレー)
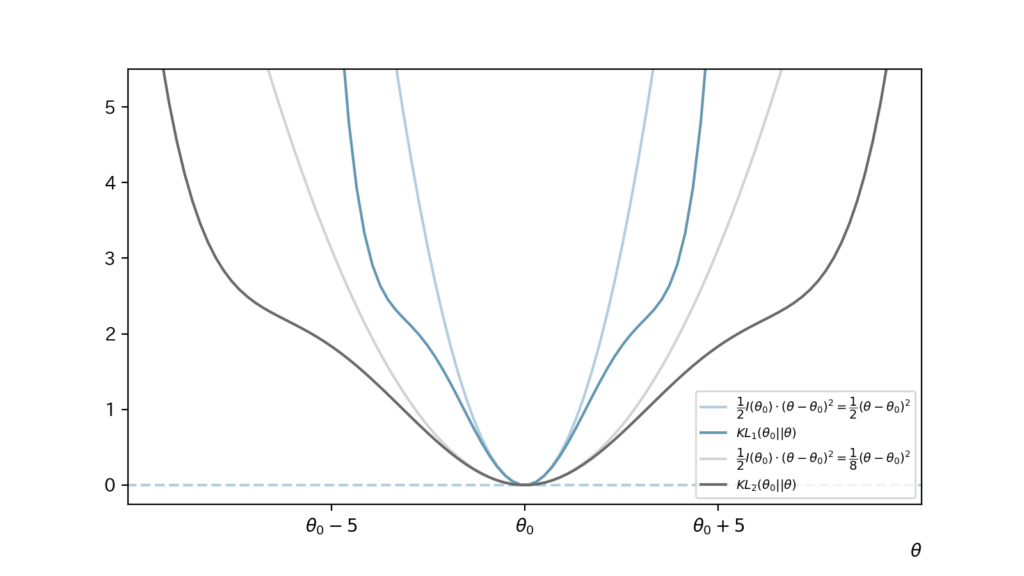
- (上記つづき)
つまり同じ分布属に属し、かつ、分布パラメータが近い分布間の『キョリ』を考えた時、$I(\theta_0)$が大きい場合には分布間の『キョリ』$KL(\theta_0||\theta)$が大きくなります。よって、分布間の識別がしやすくなり、(分布パラメータの)推定量の推定精度が高くなります。
(↑青・薄青に相当)
一方で、$I(\theta_0)$が小さい場合には分布間の『キョリ』$KL(\theta_0||\theta)$が小さくなります。よって、分布間の識別がしずらくなり、(分布パラメータの)推定量の推定精度が低くなります。
(↑グレー・薄グレーに相当) - 分布間の『キョリ』を考えてきましたが、考えてきた内容をFigでまとめて終わります。
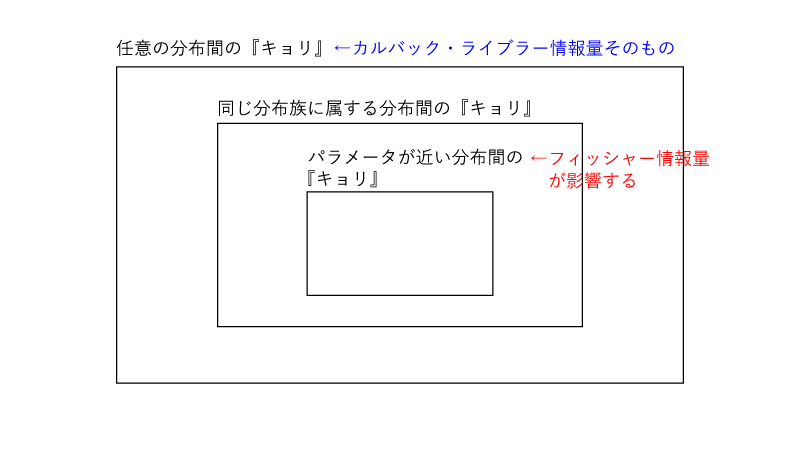
まとめ.
- カルバック・ライブラー情報量とは分布間の『キョリ*』である。
- カルバック・ライブラー情報量を任意の分布間の『キョリ*』とすると、フィッシャー情報量は分布パラメータが近い分布間の『キョリ*』に影響する因子となる。
(*:通常の「距離」とは異なる)






