$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}} \\ \gdef \indep {\mathop{\perp\!\!\!\!\perp}} \\ \gdef \tr {\mathrm{tr}}$
『主成分分析』についての知識が全くないのですが、これはどういった手法でしょうか?
『主成分分析』とは、多くの変数についての情報をより少ない合成変数に縮約し合成変数を以てデータを記述する手法です。
なるほどです。その合成変数とはどの様に産み出されるのでしょうか?
以下の2つの条件を満たす様に合成変数を産み出します。
①元の変数の線型結合で表される
②標本のばらつきを最大限反映する
具体的な産み出し方は以下確認していきましょう。
0. (準備)データの前処理(中心化、標準化)
主成分分析における合成変数の前処理として、中心化と標準化を紹介します。
0-1. 中心化
『中心化』とは、平均ベクトルがゼロベクトルとなる様にする変換です。
具体的には、サンプルサイズ$n$の標本を対象に$p$個の変数を収集した時、以下の様にデータが得られたとします。

この時、中心化をすると、

となります。
また、Figで示すと以下のFig0-1の様になります。
Fig0-1.

Figを見るとわかりますが、中心化とは標本の平行移動、に過ぎないですね。
0-2. 標準化
『標準化』とは、平均ベクトルがゼロベクトルに、かつ、各変数における分散が1となる様にする変換です。
具体的には、上記と同じデータが得られたとき、標準化をすると、
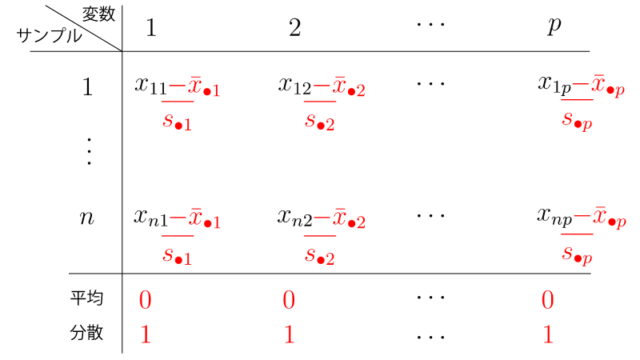
となります。
また、Figで示すと以下のFig0-2の様になります。
Fig0-2.

Figを見るとわかりますが、標準化とは標本の平行移動(中心化)+伸び縮み、に過ぎないですね。
0-3. 主成分分析の文脈における中心化・標準化
データの前処理として『中心化』を行った場合も行わなかった場合は、主成分分析において産み出される合成変数は変わりません。
一方で、データの前処理として『標準化』を行った場合と行わなかった場合とでは、主成分分析において産み出される合成変数は変わります。
例えば『身長(m)』『体重(kg)』という2つの変数を考えた時、前者はおおよそ$1.0$から$2.0$、後者はおおよそ$30$から$100$の範囲に収まるでしょう。
よって『体重(kg)』の方がスケールが大きいため、『体重(kg)』の標本のばらつき(分散)がより大きくなると考えられます。
主成分分析では標本のばらつき(分散)を最大化する様に合成変数が産み出されますが、データの前処理をしない場合には、『体重(kg)』の方が重視されることになります。
データの前処理として『中心化』をした場合にもこれは変わりませんが、もしデータの前処理として『標準化』をした場合には、『身長(m)』『体重(kg)』どちらの分散も1に揃うため『体重(kg)』の方が重視されることはなくなります。
(注意)
一般的にはデータの前処理として『中心化』ないし『標準化』を行なった上で、合成変数を産み出します。そこで、以下ではデータの前処理として『中心化』ないし『標準化』をすでに行なってある状況での話をします。 なお、『中心化』と『標準化』のどちらが望ましいかは一概に言えるものではなく、取り組む問題によって検討します。
1. 主成分分析の概略
(以下ではデータの前処理としての中心化ないし標準化がすでにされてるものとします)
サンプルサイズ$n$の標本を対象に$p$個の変数を収集したとします。
この時、
$$\begin{aligned} \vec x_i = (x_{i1}, x_{i2}, \cdots, x_{ip})^{\top} ~~ \small{(i=1, \cdots, n)} \end{aligned}$$とします。
主成分分析の流れは以下のとおりです。
まず新しい軸$\vec u$に対して$\vec x$($p$次元)を射影することで、射影後の大きさ$\vec x^{\top} \vec u$($1$次元)を得ます。(データを$p$次元から$1$次元に縮約)
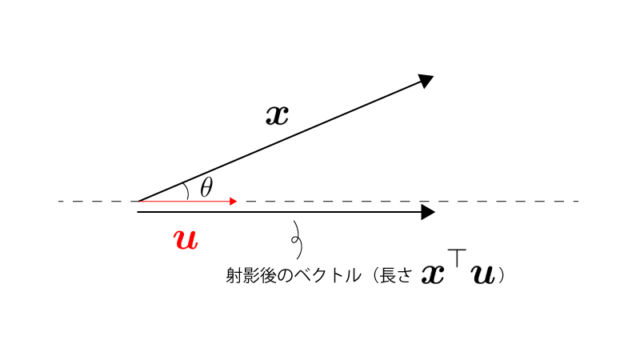
$\vec u$(つまり軸)の選び方によって射影後の大きさ$\vec x^{\top} \vec u$は異なりますが、$\{ \vec x_i^{\top} \vec u_1 \} ~~ \small{(i=1,\cdots,n)}$の分散を最大化する$\vec u$を見つけます。(別の言い方をすると、データの違いが最も際立つ様な新たな軸を見つけます)
具体的には以下の通りです。
step 1) $1$個めの軸を見つける
$\vec x_i \Rightarrow \vec x_i^{\top} \vec u_1$、と射影した時に、$\{ \vec x_i^{\top} \vec u_1 \} ~~ \small{(i=1,\cdots,n)}$の分散を最大化するベクトル$\vec u_1$(ただし$|| \vec u_1 || = 1$)を見つけます。
step 2) $2$個めの軸を見つける
$\vec x_i \Rightarrow \vec x_i^{\top} \vec u_2$、と射影した時に、$\{ \vec x_i^{\top} \vec u_2 \} ~~ \small{(i=1,\cdots,n)}$の分散を最大化するベクトル$\vec u_2$(ただし$|| \vec u_2 || = 1, \color{red}{ \vec u_2 \perp \vec u_1 }$)を見つけます。
step 3) $3$個めの軸を見つける
$\vec x_i \Rightarrow \vec x_i^{\top} \vec u_3$、と射影した時に、$\{ \vec x_i^{\top} \vec u_3 \} ~~ \small{(i=1,\cdots,n)}$の分散を最大化するベクトル$\vec u_3$(ただし$|| \vec u_3 || = 1, \color{red}{ \vec u_3 \perp \vec u_1, \vec u_3 \perp \vec u_2 }$)を見つけます。
step 4) $4$個めの軸を見つける
(省略)
・・・
step p) $p$個めの軸を見つける
(省略)
step (p+1)) $\vec u_1, \cdots, \vec u_p$のうち$\vec u_1$からいくつかを用いてデータを記述する
$\vec u_1, \cdots, \vec u_p$がいわゆる『合成変数』ですね。
その通りです。元のデータのばらつきを説明する強さは$\vec u_1 \gt \vec u_2 \gt \cdots \gt \vec u_p$となっているため、$\vec u_1$からいくつかを用いてデータを記述しなおすことで、元のデータのばらつきの多くを効率よく説明することができます。
なるほどです。わかってきましたが、まだイメージが完全ではありません。
イメージについては下記の例を参照してみてください。
例1.
$20$人の高校生を対象にセンター試験3科目(英語、数学、国語)の点数を収集したとします。
この時、収集したデータを中心化した上でプロットすると以下の様でした。
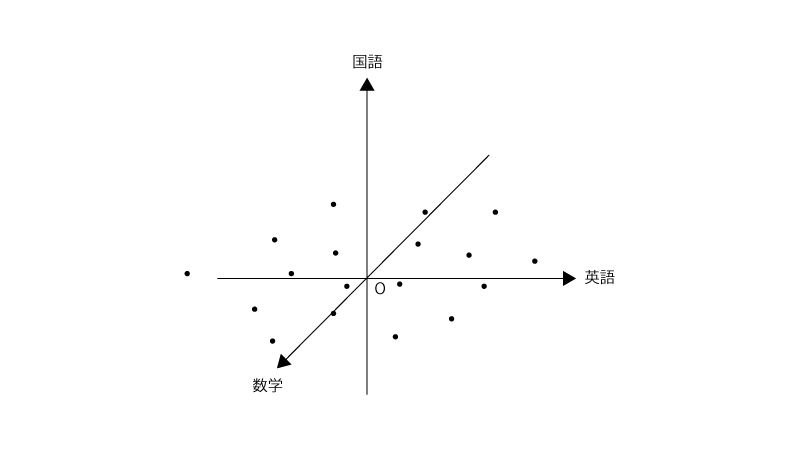
そのデータをある軸$\vec u$に射影すると以下の様になります。
(変換後の推移がわかるように、代表として1つの点を青色で表示してます)

分散を最大化する軸$\vec u_1$を見つけたら、それと同じ流れで分散を最大化する軸$\vec u_2$を見つけます。ただし、$\color{red}{\vec u_2 \perp \vec u_1}$、という条件が加わります。
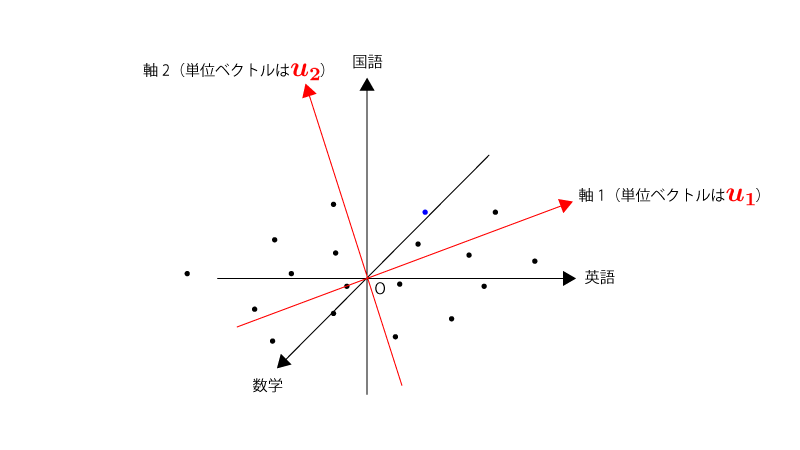
元々の変数が$3$個であるため、軸$\vec u_3$まで見つけることができます。ただし、$\color{red}{\vec u_3 \perp \vec u_1, \vec u_3 \perp \vec u_2}$、という条件が加わります。

そして、見つけてきた$\vec u_1, \vec u_2, \vec u_3$のうち$\vec u_1$からいくつかを用いてデータを記述します。
今回の場合には、①$\vec u_1$、②$\vec u_1, \vec u_2$、③$\vec u_1, \vec u_2, \vec u_3$、の$3$パターンが考えられます。
(①$\vec u_1$を用いたデータの記述)
データを軸$\vec u_1$にプロットし直すと以下の様になります。
(②$\vec u_1, \vec u_2$を用いたデータの記述)
データを軸$\vec u_1, \vec u_2$にプロットし直すと以下の様になります。

(③$\vec u_1, \vec u_2, \vec u_3$を用いたデータの記述)
データを軸$\vec u_1, \vec u_2, \vec u_3$にプロットし直すと以下の様になります。

最後の③の場合は元々のプロットと同じ空間を、軸だけ変化させた上で、見直してることになります。
イメージは掴めてきたでしょうか?射影軸を見つけるにあたっては実際にプロットしてみて見つけるわけはなく、以下『2. 主成分分析の具体的な計算』の通り計算によって見つけてきます。
2. 主成分分析の具体的な計算
(以下ではデータの前処理としての中心化ないし標準化がすでにされてるものとします)
サンプルサイズ$n$の標本を対象に$p$個の変数を収集したとします。
この時、
$$\begin{aligned} \vec x_i = (x_{i1}, x_{i2}, \cdots, x_{ip})^{\top} ~~ \small{(i=1, \cdots, n)} \end{aligned}$$とします。
まず、$\vec x_i \Rightarrow \vec x_i^{\top} \vec u_1$、と射影した時に、$\{ \vec x_i^{\top} \vec u_1 \} ~~ \small{(i=1,\cdots,n)}$の分散を最大化するベクトル$\vec u_1$(ただし$|| \vec u_1 || = 1$)を見つけます。
このためには、$|| \vec u ||^2 = 1$という条件のもとで($|| \vec u || = 1$と同値)、
$$\begin{aligned} \dfrac{1}{n-1} \sum_{i=1}^{n} (\vec x_i^{\top} \vec u)^2 \end{aligned}$$を最大化するという問題を解くことになります。
分散共分散行列$S$をここで準備しておきます。
$$\begin{aligned} S &= \dfrac{1}{n-1} \sum_{i=1}^{n} (\vec x_i-\bar{\vec x}) (\vec x_i-\bar{\vec x})^{\top} \\ &{\scriptsize (分散共分散行列の定義より。なお、\bar{\vec x} = (\bar{x}_{\bullet 1}, \bar{x}_{\bullet 2}, \cdots, \bar{x}_{\bullet p}))} \\ &= \dfrac{1}{n-1} \sum_{i=1}^{n} \vec x_i \vec x_i^{\top} \\ &{\scriptsize(今回はデータの前処理として中心化ないし標準化してあるため\bar{\vec x}=0)} \end{aligned}$$
上記で出てきた$\frac{1}{n-1} \sum_{i=1}^{n} (\vec x_i^{\top} \vec u)^2$については下記の通り分散共分散行列$S$を用いた形に変形できます。
$$\begin{aligned} \dfrac{1}{n-1} \sum_{i=1}^{n} (\vec x_i^{\top} \vec u)^2 &= \dfrac{1}{n-1} \sum_{i=1}^{n} (\vec u^{\top} \vec x_i) (\vec x_i^{\top} \vec u) \\ &= \vec u^{\top} (\dfrac{1}{n-1} \sum_{i=1}^{n} \vec x_i \vec x_i^{\top}) \vec u \\ &= \vec u^{\top} S \vec u \end{aligned}$$
さて、この変形を加味した上で上記の最大化問題に話を戻すと、これはラグランジュの未定乗数法を適用できる状況で(参照:<ラグランジュの未定乗数法>)、
$$\begin{aligned} L_i = (\vec u^{\top} S \vec u)-\lambda (|| \vec u ||^2-1) \end{aligned}$$と置いて、$L_i$を$\vec u$で偏微分して$=0$とすると、
$$\begin{aligned} (\dfrac{\partial}{\partial \vec u} L_i) = \dfrac{\partial}{\partial \vec u} \{ (\vec u^{\top} S \vec u)-\lambda (|| \vec u ||^2-1) \} &= 0 \\ \Rightarrow 2 S \vec u-\lambda \cdot 2 \vec u &= 0 \\ \Rightarrow S \vec u &= \lambda \vec u ~~~~~ \mathrm{(A)} \end{aligned}$$となり、これは固有値問題に相当します。
まとめると、主成分分析における射影軸$\vec u$の導出は、分散共分散行列(ないし相関行列)の固有値問題に帰着されるわけです。
$\mathrm{(A)}$に左から$\vec u^{\top}$を作用させると、
$$\begin{aligned} \vec u^{\top} S \vec u &= \lambda \vec u^{\top} \vec u \\ &= \lambda || \vec u ||^2 \\ &= \lambda \\ &{\scriptsize(|| \vec u ||=1より)} \end{aligned}$$となり、固有ベクトル$\vec u$に対する固有値$\lambda$そのものが、軸$\vec u$に射映した際の分散($\vec u^{\top} S \vec u = \frac{1}{n-1} \sum_{i=1}^{n} (\vec x_i^{\top} \vec u)^2$)に相当することがわかります。
そのため、$\mathrm{(A)}$を解いて出てくる固有ベクトル$\vec u$のうち、最大の固有値$\lambda$に対応する固有ベクトル$\vec u$が求める射影軸1となります。
続いて、射影軸1と直行するという条件の下で、射影した時の分散を最大化する射影軸2を見つけたいのですが、実は$\mathrm{(A)}$を解いて出てくる固有ベクトルのうち、$2$番目に大きな固有値$\lambda$に対応する固有ベクトル$\vec u$が求める射影軸2となります。
さらに、射影軸1,2と直行するという条件の下で、射影した時の分散を最大化する射影軸3を見つけたいのですが、実は$\mathrm{(A)}$を解いて出てくる固有ベクトルのうち、$3$番目に大きな固有値$\lambda$に対応する固有ベクトル$\vec u$が求める射影軸3となります。
(以下同様のため省略)
この理由について興味がある方は、<補足. 主成分分析>を参照ください。
3. 主成分分析まわりの用語
3-1. 主成分と主成分得点
一般のデータ$\vec x = (x_1, \cdots, x_p)^{\top}$、$j$個目$(j=1, \cdots, p)$の射影軸に対して、
$$\begin{aligned} y_j = \{ \vec x^{\top} \vec u_j \} \end{aligned}$$を『第$j$主成分』と言います。
また、各観測$\vec x_i$を$\vec x$に代入した、
$$\begin{aligned} \{ \vec x_i^{\top} \vec u_j \} \end{aligned}$$を『(観測$i$の)第$j$主成分得点』と言います。
3-2. 寄与率と累積寄与率
(『2. 主成分分析の具体的な計算』で使用した記号を引き継ぎます)
求めた射影軸(ベクトル)$\vec u_1,\cdots, \vec u_p$とそれぞれに対応する固有値を$\lambda_1, \cdots, \lambda_p ~~ \small{(\lambda_1 \gt \cdots \gt \lambda_p)}$として、
$$\begin{aligned} U = (\vec u_1, \cdots, \vec u_p) ~~~~ (\in \mathrm{\vec R}^{p \times p}) \end{aligned}$$とします。
すると先ほどの固有値問題は、
$$\begin{aligned} U^{\top} S U = \begin{pmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & \lambda_p \end{pmatrix} \end{aligned}$$とまとめることができます。
この時、上式のtraceをとると、
$$\begin{aligned} \tr(U^{\top} S U) &= \tr \begin{pmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & \lambda_p \end{pmatrix} \\ &= \lambda_1 + \cdots + \lambda_p ~~~~~ \mathrm{(B)} \end{aligned}$$となります。
一方で、$\tr(U^{\top} S U)$について、
$$\begin{aligned} \tr(U^{\top} S U) &= \tr(S U U^{\top}) \\ &= \tr(S) \\ &{\scriptsize(|| \vec u_i ||^2 = 1 (i=1, \cdots, n)と\vec u_i^{\top} \vec u_j = 0 (i \neq j)よりU U^{\top}=I)} ~~~~~ \mathrm{(C)} \end{aligned}$$となります。
そもそもの$\tr(S)$は分散共分散行列$S$の対角成分の総和(つまり、各変数についての分散の総和)を表すことと、$\mathrm{(B)}, \mathrm{(C)}$より、
$$\begin{aligned} {\small(元の各変数についての分散の総和)} = \lambda_1 + \cdots + \lambda_p \end{aligned}$$が成立します。
データの分散についてのイメージ図は下記のようになります。
(ただし、元の変数を$4$個としてます)

$(\lambda_1 + \cdots + \lambda_p)$は変数の分散の総和に一致しましたが、$(\lambda_1 + \cdots + \lambda_p)$において$\lambda_j ~~ {\small(j=1, \cdots, p)}$が占める割合を『第$j$主成分の寄与率』と言います。
また、$(\lambda_1 + \cdots + \lambda_p)$において$(\lambda_1 + \cdots + \lambda_j) ~~ {\small(j=1, \cdots, p)}$が占める割合を『第$j$主成分までの累積寄与率』と言います。
すなわち、
$$\begin{aligned} {\small(第j主成分の寄与率)} &= \frac{\lambda_j}{\lambda_1+\cdots+\lambda_p} \\[10px] {\small(第j主成分までの累積寄与率)} &= \frac{\lambda_1 + \cdots + \lambda_j}{\lambda_1+\cdots+\lambda_p} \end{aligned}$$となります。
例3.
上記Figでは
・第$1$主成分の寄与率:$60$%
・第$2$主成分の寄与率:$30$%
であり、
・第$1$主成分までの寄与率:$60$%
・第$2$主成分までの寄与率:$90$%
となります。
つまり、第$2$主成分までで分散の$90$%を説明できており、元の$4$つの変数を$2$つの変数に縮約しても大きく問題なさそうですね。
3-3. 主成分負荷量
第$j$主成分$y_j$と元の変数$x_k ~~ {\small(k=1, \cdots, p)}$との相関係数$\gamma_{j,k}$を求めることで(さらにはプロットすることで)、第$j$主成分のおおよその解釈が可能となります。
『第$j$主成分$y_j$と元の変数$x_k ~~ {\small(k=1, \cdots, p)}$との相関係数』を『(第$j$主成分における変数$x_k$の)主成分負荷量』と言います。
つまり、
$$\begin{aligned} \gamma_{j,k} = \frac{\Cov[y_j, x_k]}{\sqrt{V[y_j] V[x_k]}} \end{aligned}$$となります。
『主成分負荷量』とは主成分と元の変数との相関係数に過ぎないので、あまり難しく考えないでください。
補足.
固有値問題$\mathrm{(A)}$に戻ってみると、
$$\begin{aligned} \lambda_j \vec u_j &= S \vec u_j \\ &= \frac{1}{n-1} \sum_{i=1}^{n} \vec x_i \vec x_i^{\top} \vec u_j \\ &{\scriptsize(ただしデータは中心化してあるものとし、\bar{\vec x}=\vec 0とした)} \\ &= \frac{1}{n-1} \sum_{i=1}^{n} \vec x_i y_{i,j} \\ &= \begin{pmatrix} \Cov[x_1, y_j] \\ \vdots \\ \Cov[x_p, y_j] \end{pmatrix} \end{aligned}$$が成立し、この第$k$行目に着目すると、
$$\begin{aligned} \Cov[x_k, y_j] = \lambda_j u_{k,j} \end{aligned}$$となります。
これより$\gamma_{j,k}$について、
$$\begin{aligned} \gamma_{j,k} &= \frac{\Cov[y_j, x_k]}{\sqrt{V[y_j] V[x_k]}} \\ &= \frac{\lambda_j u_{k,j}}{\sqrt{\lambda_j V[x_k]}} \\ &{\scriptsize(\Cov[x_k, y_j]=\lambda_j u_{k,j}, V[y_j]=\lambda_j)} \\ &= \frac{\sqrt{\lambda_j} u_{k,j}}{\sqrt{V[x_k]}} \end{aligned}$$となります。
例4.
20人の高校生を対象に、センター試験5科目(英語、数学、国語、物理、化学)の点数を収集した。 主成分分析として、第$1$主成分、第$2$主成分における元の変数(英語、数学、国語、物理、化学)の主成分負荷量をプロットしたところ下記の通りとなった。
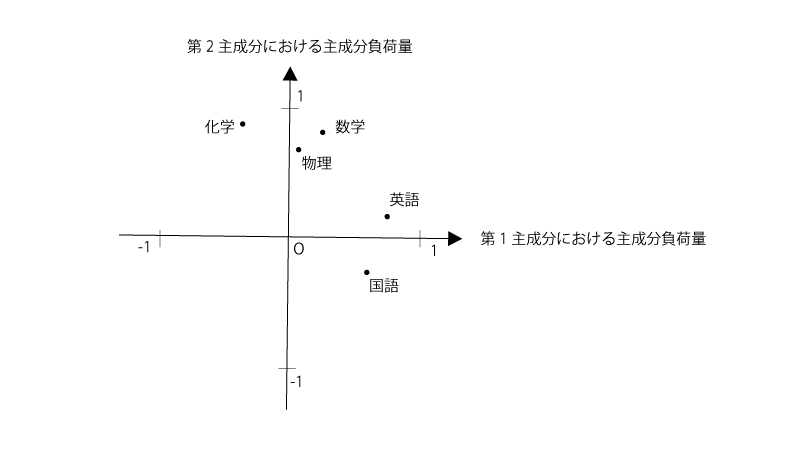
この時、第$1$主成分における主成分負荷量は英語と国語で高くなっていることから、第$1$主成分を『文系科目』と解釈できる。
また、第$2$主成分における主成分負荷量は数学、物理、化学で高くなっていることから、第$2$主成分を『理系科目』と解釈できる。
例題1.
20人の高校生を対象に、センター試験5科目(英語、数学、国語、物理、化学)の点数を収集した。
主成分分析として、各生徒の第$1$主成分、第$2$主成分の主成分得点をプロットしたところ下記の通りとなった。また第$1$主成分、第$2$主成分における元の変数(英語、数学、国語、物理、化学)の主成分負荷量もプロットした。
(注意:各サンプルの主成分得点をプロットしたものの個数はサンプルサイズである。一方で、第$1$主成分、第$2$主成分における元の変数の主成分負荷量をプロットしたものの個数は元の変数の個数である。)

(1). 第$1$主成分、第$2$主成分についての解釈を与えよ。
(2). 丸がついた4人の生徒が同じ大学を受験したものとする。この時、いずれの生徒が合格したと考えられるか?
解答.
(1). 第$1$主成分における主成分負荷量は理系科目で高くなっていることから、第$1$主成分を『理系科目』と解釈できる。第$2$主成分における主成分負荷量は文系科目で高くなっていることから、第$2$主成分を『文系科目』と解釈できる。
(2). 『理系科目』と解釈できる第$1$主成分は右側ほどその能力が高く、『文系科目』と解釈できる第$2$主成分は下側ほどその能力が高い。A~DのうちでBがどちらの能力も高いことがプロットからわかるため、Bが合格したものと考えるのが妥当である。
まとめ.
- 『主成分分析』とは、多くの変数についての情報をより少ない合成変数に縮約し合成変数を以てデータを記述する手法である。
- データを合成変数に縮約する際のルールとしては、元の分散を最大限説明できるように合成変数を順に作成していく、というものである。






