確率変数の変数変換

• *：実のところは、後出の「ヤコビ行列」の行列式$(\det)$を「ヤコビアン」と呼びますが、上記はその1次元の場合です。
  
  
• $\mathrm{(A)}$における”$\displaystyle \frac{dx}{dy}$”の部分は注意が必要で、”$\displaystyle \frac{dy}{dx}$”ではありません！
  以下の様な覚え方がおすすめです。

（覚え方）
確率密度関数の積分は$1$なので、$$ \begin{aligned} (1 =) \int f_X(x)dx = \int f_Y(y)dy \end{aligned}$$ 上式の$\displaystyle \int$の中身だけとり出して、$$ \begin{aligned} f_X(x) dx = f_Y(y) dy \end{aligned}$$ 両辺を$dy$で割って（そしてさっと絶対値をつけて）$$ \begin{aligned} f_Y(y) = f_X(x) \cdot \left|\frac{dx}{dy} \right| \end{aligned} $$

例題1.
確率変数$X$は$\mathrm{N}(\mu, \sigma^2)$に従う、即ち、$X$の確率密度関数$f_X(x)$は $$ \begin{aligned} f_X(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left[- \frac{(x – \mu)^2}{2 \sigma^2} \right] \end{aligned} $$とする。
$Y = \exp(X)$として新たな確率変数$Y$を産み出した時、 $Y$の確率密度関数$f_Y(y)$を求めよ。

解答.
$y = \exp(x)$より$x = \log y ~~(y \gt 0)$ 両辺を$y$で微分して、$$ \begin{aligned} \frac{dx}{dy} = \frac{1}{y} \end{aligned}$$となる。

よって、 $$ \begin{aligned} f_Y(y) &= f_X(x) \cdot \left| \frac{dx}{dy} \right| \\ &= \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left[- \frac{(x – \mu)^2}{2 \sigma^2} \right] \cdot \left| \frac{1}{y} \right| \\ &\scriptsize{(上式より)} \\ &= \frac{1}{\sqrt{2 \pi \sigma^2}y} \exp \left[- \frac{(\log y – \mu)^2}{2 \sigma^2} \right] ~~ \small{(y \gt 0)} \end{aligned}$$ と求められる。

• ここでは確率ベクトルが2次元の場合を扱っていますが、3次元以上の場合も同様に考えられます。
  
  
  
• $\vec P = \begin{pmatrix} X_1 \\ X_2 \end{pmatrix} \longrightarrow \vec Q = \begin{pmatrix} Y_1 \\ Y_2 \end{pmatrix}$という変換においては、$Y_1, Y_2$はそれぞれ「$X_1, X_2$の関数」となっています。「$Y_1$は$X_1$の関数、$Y_2$は$X_2$の関数」というのは間違いなので注意してください。
  
  
  
• ヤコビ行列は通常”$J$”や”$J \left(\displaystyle \frac{ \partial \vec p }{ \partial \vec q } \right)$”と表記されます。
  
  
  
• ヤコビ行列$J \left(\displaystyle \frac{ \partial \vec p }{ \partial \vec q } \right)$は$\begin{pmatrix} \displaystyle \frac{\partial x_1}{\partial y_1} & \displaystyle \frac{\partial x_1}{\partial y_2} \\ \displaystyle \frac{\partial x_2}{\partial y_1} & \displaystyle \frac{\partial x_2}{\partial y_2} \end{pmatrix}$ですが、最終的には行列式をとるので、もしも$\begin{pmatrix} \displaystyle \frac{\partial x_1}{\partial y_1} & \displaystyle \frac{\partial x_2}{\partial y_1} \\ \displaystyle \frac{\partial x_1}{\partial y_2} & \displaystyle \frac{\partial x_2}{\partial y_2} \end{pmatrix}$と勘違いしてしまってもヤコビアンの値は同一になります。
  
  
  
• $X \rightarrow Y$という「確率変数の変数変換」の場合には、ヤコビ行列に相当するのは”$\displaystyle \frac{dx}{dy}$”でしたが$\det \left(\displaystyle \frac{dx}{dy} \right) = \displaystyle \frac{dx}{dy}$なので、つまるところ「確率変数の変数変換」は「確率ベクトルの変数変換」の特殊例とみなすことができます。

例題2.
確率変数$X, Y$は互いに独立に正規分布$\mathrm{N}(\mu, \sigma^2)$に従うとする。
ここで、$$ \begin{aligned} X = R \cos \Theta \\ Y = R \sin \Theta \end{aligned}$$ という$\begin{pmatrix} X \\ Y \end{pmatrix} \longrightarrow \begin{pmatrix} R \\ \Theta \end{pmatrix}$なる確率ベクトルの変数変換を考える。
この時、確率ベクトル$\begin{pmatrix} R \\ \Theta \end{pmatrix}$の（同時）確率密度関数を求めよ。

（注意：$R, \Theta$は$r, \theta$の大文字）

解答.
$X, Y$の確率密度関数を$f_X(x), f_Y(y)$とすると、$$ \begin{aligned} f_X(x) &= \frac{1}{\sqrt{2 \pi}} \exp \left( – \frac{x^2}{2} \right) \\ f_Y(y) &= \frac{1}{\sqrt{2 \pi}} \exp \left( – \frac{y^2}{2} \right) \end{aligned} $$であるから、 $$ \begin{aligned} \small{(X, Yの同時確率密度関数)} &= f_X(x) \cdot f_Y(y) \\ &\scriptsize{(X, Yの独立性より)} \\ &= \frac{1}{2 \pi} \exp \left( – \frac{x^2 + y^2}{2} \right) \end{aligned}$$

ここでヤコビ行列$J$は、 $$\begin{aligned} J = \begin{pmatrix} \displaystyle \frac{\partial x}{\partial r} & \displaystyle \frac{\partial x}{\partial \theta} \\ \displaystyle \frac{\partial y}{\partial r} & \displaystyle \frac{\partial y}{\partial \theta} \end{pmatrix} = \begin{pmatrix} \cos \theta & -r \sin \theta \\ \sin \theta & r \cos \theta \end{pmatrix} \end{aligned} $$であるから、ヤコビアン$\det J$の絶対値は、$$ \begin{aligned} |\det J| &= \left| \det \begin{pmatrix} \cos \theta & -r \sin \theta \\ \sin \theta & r \cos \theta \end{pmatrix} \right| \\ &= | \cos \theta \cdot r \cos \theta – (-r \sin \theta) \cdot \sin \theta| \\ &= |r(\cos^2 \theta + \sin^2 \theta)| \\ &= r \end{aligned}$$

よって、 $$\begin{aligned} \small{(R, \Thetaの同時確率密度関数)} &= \small{(X, Yの同時確率密度関数)} \times |\det J| \\ &= \frac{1}{2 \pi} \exp \left( – \frac{x^2 + y^2}{2} \right) \cdot r \\ &= \frac{r}{2 \pi} \exp \left(- \frac{r^2}{2} \right) ~~ \small{(r \geqq 0, ~0 \leqq \theta \leqq 2 \pi)} \end{aligned} $$と求められる。

（示すべき内容）
確率ベクトル$\vec P, \vec Q$に対して、 $$ \begin{aligned} &\vec P \sim f_{\vec P}(\vec p) \\ &\vec Q \sim f_{\vec Q}(\vec q) \\ &\vec P \overset{\displaystyle {g}}\longrightarrow \vec Q \end{aligned} $$（ただしこの変換$g$は微分可能で、$\vec P$と$\vec Q$を$1:1$に結びつける変換であるとします。即ち、$g^{-1}$が存在するとします。）
である時、$$ \begin{aligned} f_{\vec Q}(\vec q) = f_{\vec P}(\vec p) \cdot \left| \det \left( J \left(\frac{ \partial \vec p }{ \partial \vec q } \right) \right) \right| ~~~~~\mathrm{(B)} \end{aligned}$$

（簡易的な証明）
ある微小空間$A = [y_1, ~y_1 + \Delta y_1] \times \cdots \times [y_d, ~y_d + \Delta y_d]$に$(\vec Q =) \vec q$が入る確率を考えると、$$ \begin{aligned} f_{\vec Q}(\vec q) \cdot m(A) &\fallingdotseq Pr\{\vec q \in A \} \\ &\scriptsize{(ただしm(A)はAの面積ないし体積)} \\[5px] &= Pr\{ g^{-1}(\vec q) \in g^{-1}(A) \} \\[5px] &= Pr\{ \vec p \in B \} \\ &\scriptsize{(ただしB:= g^{-1}(A))} \\[5px] &\fallingdotseq f_{\vec P}(\vec p) \cdot m(B) ~~~~~\mathrm{(C)} \\ &\scriptsize{(ただしm(B)はBの面積ないし体積)} \end{aligned} $$となる。

以下簡単のために$d=2$の場合を考える。（$d \geqq 3$の場合も同様に考えられる）
即ち、以下の様な設定とする。

Fig1.

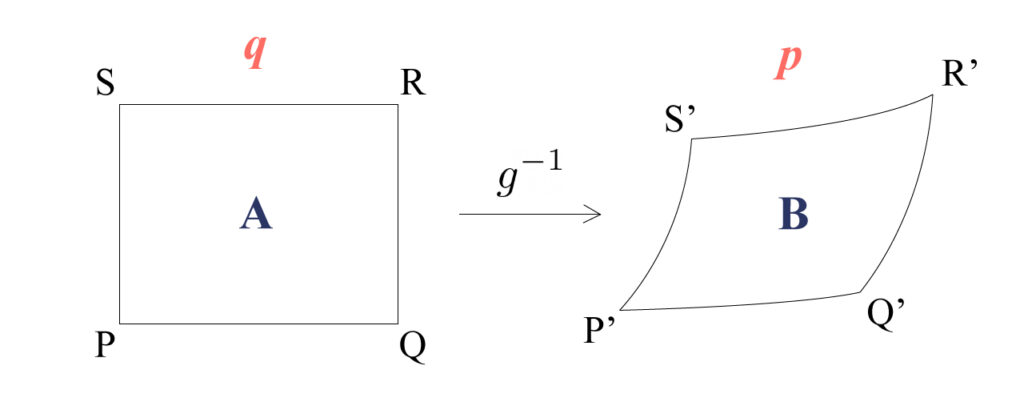
$$ \begin{aligned} P &= (y_1, y_2) \\ Q &= (y_1 + \Delta y_1, y_2) \\ R &= (y_1 + \Delta y_1, y_2 + \Delta y_2) \\ S &= (y_1, y_2 + \Delta y_2) \end{aligned}$$
この時、$m(B)$は$\overrightarrow{ P^{\prime} Q^{\prime} }, \overrightarrow{ P^{\prime} S^{\prime} }$を辺とする平行四辺形の面積とほぼ等しく、これは$| \det (\overrightarrow{ P^{\prime} Q^{\prime} }, \overrightarrow{ P^{\prime} S^{\prime} }) |$で表される。

よって、$$ \begin{aligned} \overrightarrow{ P^{\prime} Q^{\prime} } &= \overrightarrow{ O Q^{\prime} } – \overrightarrow{ O P^{\prime} } \\[5px] &= \begin{pmatrix} x_1(y_1 + \Delta y_1, y_2) – x_1(y_1, y_2) \\ x_2(y_1 + \Delta y_1, y_2) – x_2(y_1, y_2) \end{pmatrix} \\ &\scriptsize{(媒介変数様に表示している)} \\[5px] &\fallingdotseq \begin{pmatrix} \displaystyle \frac{\partial x_1}{\partial y_1} (y_1, y_2) \times \Delta y_1 \\ \displaystyle \frac{\partial x_2}{\partial y_1} (y_1, y_2) \times \Delta y_1 \end{pmatrix} \\ &\scriptsize{(テーラー展開より)} \end{aligned} $$ $$ \begin{aligned} \overrightarrow{ P^{\prime} S^{\prime} } &= \overrightarrow{ O S^{\prime} } – \overrightarrow{ O P^{\prime} } \\[5px] &= \begin{pmatrix} x_1(y_1, y_2 + \Delta y_2) – x_1(y_1, y_2) \\ x_2(y_1, y_2 + \Delta y_2) – x_2(y_1, y_2) \end{pmatrix} \\ &\scriptsize{(媒介変数様に表示している)} \\[5px] &\fallingdotseq \begin{pmatrix} \displaystyle \frac{\partial x_1}{\partial y_2} (y_1, y_2) \times \Delta y_2 \\ \displaystyle \frac{\partial x_2}{\partial y_2} (y_1, y_2) \times \Delta y_2 \end{pmatrix} \\ &\scriptsize{(テーラー展開より)} \end{aligned} $$を考慮すると、$m(B)$は$$ \begin{aligned} m(B) &\fallingdotseq \left| \det \begin{pmatrix} \displaystyle \frac{\partial x_1}{\partial y_1} \times \Delta y_1 & \displaystyle \frac{\partial x_1}{\partial y_2} \times \Delta y_2 \\ \displaystyle \frac{\partial x_2}{\partial y_1} \times \Delta y_1 & \displaystyle \frac{\partial x_2}{\partial y_2} \times \Delta y_2 \end{pmatrix} \right| \\[20px] &= \left| \det \begin{pmatrix} \displaystyle \frac{\partial x_1}{\partial y_1} & \displaystyle \frac{\partial x_1}{\partial y_2} \\ \displaystyle \frac{\partial x_2}{\partial y_1} & \displaystyle \frac{\partial x_2}{\partial y_2} \end{pmatrix} \right| \times \Delta y_1 \Delta y_2 \\[20px] &= \left| \det \left( J \left(\frac{ \partial \vec p }{ \partial \vec q } \right) \right) \right| \times m(A) \end{aligned} $$これと$\mathrm{(C)}$から$\mathrm{(B)}$が導出される。

例題3.
確率変数$X, Y$は互いに独立に正規分布$\mathrm{N}(0, 1)$に従うとする。
この時、$(X+Y)$の確率密度関数を求めよ。

解答.
$$ \begin{aligned} \begin{pmatrix} W \\ Z \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 1 & 1 \end{pmatrix} \begin{pmatrix} X \\ Y \end{pmatrix} \end{aligned}$$という確率ベクトルの変数変換を考えると、$$ \begin{aligned} X &= W \\ Y &= Z – W \end{aligned}$$であるから、ヤコビ行列$J$は、$$ \begin{aligned} J = \begin{pmatrix} \displaystyle \frac{\partial x}{\partial w} & \displaystyle \frac{\partial x}{\partial z} \\ \displaystyle \frac{\partial y}{\partial w} & \displaystyle \frac{\partial y}{\partial z} \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ -1 & 1 \end{pmatrix} \end{aligned}$$

よって、ヤコビアン$\det J$の絶対値は、$$ \begin{aligned} |\det J| &= \left| \det \begin{pmatrix} 1 & 0 \\ -1 & 1 \end{pmatrix} \right| \\ &= 1 \end{aligned}$$

以上より、$$ \begin{aligned} \small{(W, Zの同時確率密度関数)} &= \small{(X, Yの同時確率密度関数)} \times |\det J| \\[5px] &= \left\{\frac{1}{\sqrt{2 \pi}} \exp \left( – \frac{x^2}{2} \right) \right\} \left\{\frac{1}{\sqrt{2 \pi}} \exp \left( – \frac{y^2}{2} \right) \right\} \times 1 \\ &\scriptsize{(X, Yの独立性より)} \\[5px] &= \frac{1}{2 \pi} \exp\left(- \frac{x^2 + y^2}{2} \right) \\[5px] &= \frac{1}{2 \pi} \exp\left(- \frac{w^2 + (z-w)^2}{2} \right) \end{aligned}$$

よって、$$ \begin{aligned} \small{(Zの確率密度関数)} &= \int_{- \infty}^{\infty} \frac{1}{2 \pi} \exp\left(- \frac{w^2 + (z-w)^2}{2} \right) dw \\[5px] &= \frac{1}{2 \pi} \int_{- \infty}^{\infty} \exp \left( -(w – \frac{z}{2})^2 – \frac{z^2}{4} \right) dw \\[5px] &= \frac{1}{2 \pi} \exp \left( – \frac{z^2}{4} \right) \int_{- \infty}^{\infty} \exp \left( -(w – \frac{z}{2})^2 \right) dw \\[5px] &= \frac{1}{2 \pi} \exp \left( – \frac{z^2}{4} \right) \int_{- \infty}^{\infty} \exp (- w^{\prime 2}) dw^{\prime} \\ &\scriptsize{(w^{\prime} = w – \frac{z}{2}とおいた)} \\[5px] &= \frac{1}{2 \pi} \exp \left( – \frac{z^2}{4} \right) \cdot \sqrt{\pi} \\ &\scriptsize{(ガウス積分より)} \\[5px] &= \frac{1}{\sqrt{2 \pi \cdot 2} } \exp \left( – \frac{x^2}{2 \cdot 2} \right) \end{aligned}$$となる。


（確率密度関数の形から$(Z=)X+Y$は正規分布$\mathrm{N}(0, 2)$に従うことがわかります）

（証明）
$\vec p = g^{-1}(g(\vec p))$の関係より、$$ \begin{alignat}{2} &&I &= J\left( \frac{\partial \vec p}{\partial \vec q} \right) J\left( \displaystyle \frac{\partial \vec q}{\partial \vec p} \right) \notag \\ && &\scriptsize{(ただしIは単位行列)} \notag \\[5px] &\Rightarrow & \det I &= \det \left( J\left( \frac{\partial \vec p}{\partial \vec q} \right) J\left( \displaystyle \frac{\partial \vec q}{\partial \vec p} \right) \right) \notag \\[5px] &\Rightarrow & 1 &= \det \left( J\left( \frac{\partial \vec p}{\partial \vec q} \right) \right) \cdot \det \left( J\left( \displaystyle \frac{\partial \vec q}{\partial \vec p} \right) \right) \notag \\ && &\scriptsize{(一般に\det AB = \det A \cdot \det B)} \notag \\[5px] &\Rightarrow & \det \left( J\left( \frac{\partial \vec p}{\partial \vec q} \right) \right) &= \frac{1}{\det \left( J\left( \displaystyle \frac{\partial \vec q}{\partial \vec p} \right) \right)} \notag \end{alignat}$$

例1.
互いに独立な確率変数$X, Y$から新たな確率変数$Z=aX + bY$を産み出すとする。
即ち、$$ \begin{aligned} \begin{pmatrix} W \\ Z \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ a & b \end{pmatrix} \begin{pmatrix} X \\ Y \end{pmatrix} \end{aligned} $$なる$$ \begin{aligned} \vec P = \begin{pmatrix} X \\ Y \end{pmatrix} \longrightarrow \vec Q = \begin{pmatrix} W \\ Z \end{pmatrix} \end{aligned} $$という確率ベクトルの変数変換を考える。

1. 直接的に$\det \left( J\left(\displaystyle \frac{\partial \vec p}{\partial \vec q} \right) \right)$を求める場合

$$ \begin{aligned} X &= W \\ Y &= – \frac{a}{b} W + \frac{1}{b} Z \end{aligned}$$であるから、$J\left(\displaystyle \frac{\partial \vec p}{\partial \vec q} \right)$は、$$ \begin{aligned} J\left(\displaystyle \frac{\partial \vec p}{\partial \vec q} \right) &= \begin{pmatrix} \displaystyle \frac{\partial x}{\partial w} & \displaystyle \frac{\partial x}{\partial z} \\ \displaystyle \frac{\partial y}{\partial w} & \displaystyle \frac{\partial y}{\partial z} \end{pmatrix} \\ &= \begin{pmatrix} 1 & 0 \\ – \displaystyle \frac{a}{b} & \displaystyle \frac{1}{b} \end{pmatrix} \end{aligned} $$
よって、$$ \begin{aligned} \det \left( J\left( \frac{\partial \vec p}{\partial \vec q} \right) \right) &= \det \begin{pmatrix} 1 & 0 \\ – \displaystyle \frac{a}{b} & \displaystyle \frac{1}{b} \end{pmatrix} \\ &= \frac{1}{b} \end{aligned} $$

2. 「ヤコビアンの便利な性質」を用いて$\det \left( J\left(\displaystyle \frac{\partial \vec p}{\partial \vec q} \right) \right)$を求める場合

$$ \begin{aligned} W &= X \\ Z &= a X + b Y \end{aligned} $$であるから、$J\left(\displaystyle \frac{\partial \vec q}{\partial \vec p} \right)$は、$$ \begin{aligned} J\left(\displaystyle \frac{\partial \vec q}{\partial \vec p} \right) &= \begin{pmatrix} \displaystyle \frac{\partial w}{\partial x} & \displaystyle \frac{\partial w}{\partial y} \\ \displaystyle \frac{\partial z}{\partial x} & \displaystyle \frac{\partial z}{\partial y} \end{pmatrix} \\ &= \begin{pmatrix} 1 & 0 \\ a & b \end{pmatrix} \end{aligned}$$
これより、$$ \begin{aligned} \det \left( J\left( \frac{\partial \vec q}{\partial \vec p} \right) \right) &= \det \begin{pmatrix} 1 & 0 \\ a & b \end{pmatrix} \\ &= b \end{aligned}$$
よって、$$ \begin{aligned} \det \left( J\left( \frac{\partial \vec p}{\partial \vec q} \right) \right) &= \frac{1}{\det \left( J\left( \displaystyle \frac{\partial \vec q}{\partial \vec p} \right) \right)} \\ &= \frac{1}{b} \end{aligned}$$

まとめ.

• 変数変換された確率変数（確率ベクトル）の確率密度関数は、ヤコビアンを用いて導出できる。
  
  
• 互いに独立な確率変数の和をとり確率密度関数を求める一手法として「たたみこみ」があり、これは確率変数の変数変換を用いたものである。