$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}} \\ \gdef \indep {\mathop{\perp\!\!\!\!\perp}} \\ \gdef \tr {\mathrm{tr}}$
ここでは逆関数法とともに有名かつ基本的なサンプリング法である『受容棄却法』を紹介します。
前回逆関数法を勉強して、とりあえず逆関数法を使えば良いかと思っていましたが、だめでしょうか?
逆関数法はシンプルかつ強力な手法ですが、分布関数の逆関数が求まらないことも多く、その様な場合には使えません。その様な場合でも、受容棄却法は使えます。
1. 受容棄却法
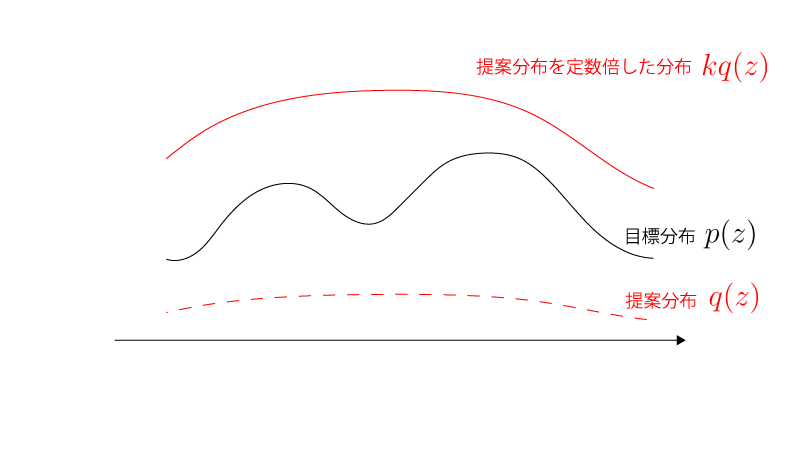
そこからサンプルしたい目的の分布(『目標分布』と言います)を$p(z)$、定数倍することで$p(z)$を上から覆うことができる分布(『提案分布』と言います)を$q(z)$とします。 これは言い換えるなれば、 ある$k$が存在してすべての$z$に対して、
$$\begin{aligned} k q(z) \geqq p(z) \end{aligned}$$とできるということです。
目標分布と提案分布の関係のイメージは以下の様なものです。
受容棄却法のアルゴリズムは以下の様になります。
for i=0,1,…,do
$~~~~$# 提案分布からサンプルする
$~~~~$sample $z^* \sim q(z)$
$~~~~$# 一定の確率でそれをaccept, reject
$~~~~$sample $u^* \sim \U[0, kq(z^*)]$
$~~~~$if $u^* \leqq p(z^*)$:accept
$~~~~$else(elif $u^* \gt p(z^*)$):reject
下記の様に目標分布と提案分布があるとして、それを的に見立てるとすれば、目標分布部分にあたればacceptし、それ以外はrejectするといったイメージです。
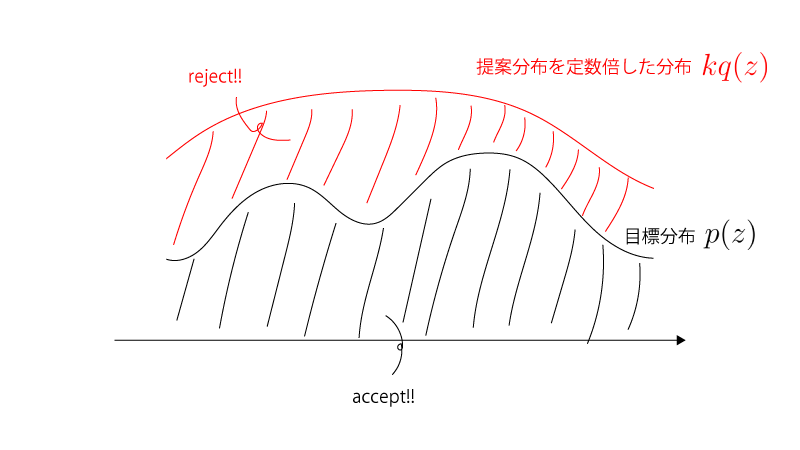
この時acceptされたサンプルは目標分布$p(z)$に従っています。以下の証明を参照してください。
(証明)
$$\begin{aligned} f(z|U \leqq \frac{p(z)}{kq(z)}) &= \frac {p(U \leqq \frac{p(z)}{k q(z)} | z) \cdot q(z)} {\int p(U \leqq \frac{p(z’)}{k q(z’)} | z’) \cdot q(z’) dz’} \\[10px] &= \frac{\frac{p(z)}{k q(z)} \cdot q(z)}{\int \frac{p(z’)}{k q(z’)} \cdot q(z’) dz’} \\[10px] &= \frac{p(z)}{1} \\[10px] &= p(z) \end{aligned}$$
ところで、定数倍$k$についてですが、提案分布$q(z)$を$k$倍したものである$k q(z)$が目標分布$p(z)$を上から覆えている必要がありました。その様な$k$はいくつも想定できますが、『$k q(z)$が$p(z)$を上から覆えていること』が保障された中でより小さい$k$の方がサンプルのaccept率が上がります。
的にしめる目標分布部分の割合が大きくなるからですね。
補足.
目標分布$p(z)$の規格化定数$C$を明示的に書くことができない場合、即ち、
$$\begin{aligned} p(z) = C \tilde{p} (z) \end{aligned}$$の$C$を明示的に書くことができない場合がよくあります。(例:ベイズの事後分布)
この様な場合でも受容棄却法は使うことができます。
補足の説明.
目標分布$p(z)$、規格化定数$C$、$\tilde{p}(z)(=\frac{p(z)}{C})$とします。
定数倍することで$\tilde{p}(z)$を上から覆うことができる、かつ、そこからサンプリング可能な分布を$q(z)$とします。(ある$k$が存在してすべての$z$に対して、$k q(z) \geqq \tilde{p}(z)$)
この時、アルゴリズムは以下の様になります。
for i=0,1,…,do
$~~~~$# 提案分布からサンプルする
$~~~~$sample $z^* \sim q(z)$
$~~~~$# 一定の確率でそれをaccept, reject
$~~~~$sample $u^* \sim \U[0, kq(z^*)]$
$~~~~$if $u^* \leqq \tilde{p}(z^*)$:accept
$~~~~$else(elif $u^* \gt \tilde{p}(z^*)$):reject
この時acceptされたサンプルは目標分布$p(z)$($\tilde{p}(z)$ではなく)に従っています。
証明.
$$\begin{aligned} f(z|U \leqq \frac{\tilde{p}(z)}{kq(z)}) &= \frac {p(U \leqq \frac{\tilde{p}(z)}{k q(z)} | z) \cdot q(z)} {\int p(U \leqq \frac{\tilde{p}(z’)}{k q(z’)} | z’) \cdot q(z’) dz’} \\[10px] &= \frac{\frac{\tilde{p}(z)}{k q(z)} \cdot q(z)}{\int \frac{\tilde{p}(z’)}{k q(z’)} \cdot q(z’) dz’} \\[10px] &= \frac{\tilde{p}(z)}{\frac{1}{C}} \\[10px] &= C \tilde{p}(z) \\[10px] &= p(z) \end{aligned}$$
まとめ.
- 受容棄却法は基本的に、目標分布$p(z)$は既知であるが(式として書き下せるが)そこからの直接のサンプリングが困難という状況を扱う。そこで、定数倍することで$p(z)$を上から覆うことができ、かつ、そこからサンプリング可能である提案分布を準備し、そこからのサンプルを一定確率でacceptする。






