$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}} \\ \gdef \indep {\mathop{\perp\!\!\!\!\perp}} \\ \gdef \tr {\mathrm{tr}}$
今回はサンプリング法の3つ目として『MCMC』ですか。
耳にしたことはありますが、その中身は全く知りません!
大丈夫です。ここではMCMCを順序立ててイメージできる様にしていきます。
まず”MCMC“とは”Markov chain Monte Carlo“の略で、マルコフ連鎖を用いたサンプリング法です。
マルコフ連鎖は以前勉強しましたね。
ただ、マルコフ連鎖がどの様にサンプリングに応用されるのか想像がつきません。
順々に説明していくので、少しずつイメージを確立してください。
補足.
・Monte Carlo法とは、乱数を用いた数値計算全般を指します。つまり、MCMCではMarcov chainで乱数を取得→何かしらの計算(Monte Carlo)をします。
・マルコフ連鎖では離散的な状態のみを扱いますが、MCMCでは連続的な状態も扱います。
0. マルコフ連鎖の復習
マルコフ連鎖は<マルコフ連鎖>でその詳細を扱いましたが、ここでは簡単に復習します。
0-1. マルコフ性とマルコフ連鎖
確率変数列$\{ X_n \} ~{\small (n=0, \cdots)}$に対して、
$$\begin{aligned} Pr\{ X_{n+1} | X_n=x_n, \ldots, X_0=x_0 \} = Pr\{ X_{n+1} | X_n=x_n \} \end{aligned}$$なる性質を「マルコフ性」と言いました。
この式は『$X_{n+1}$は直前の状態$X_n$のみから決まる』ということを表してましたね。
マルコフ性をもつ確率変数列${ X_n } ~{\small (n=0, \cdots)}$のとりうる状態が離散的である時、${ X_n }$を『マルコフ連鎖』と言いました。
0-2. 状態確率ベクトルと推移(遷移)確率行列
マルコフ連鎖における状態空間は離散的であるため、時点$n$において各状態(状態$1,…,k$)にいる確率をまとめたものをベクトル
$$\begin{aligned} \vec \pi_n = (\pi_{n,1}, \ldots, \pi_{n,k}) \end{aligned}$$
(ただし、$\sum_{l=1}^k \pi_{n,l} = 1$)
と表すことができ、これを「状態確率ベクトル」と言いました。
また、
$$\begin{aligned} \pi_{n+1} = \pi_n P \tag{A} \end{aligned}$$と時点が1ずれた状態確率ベクトルを関係づける行列$P$を「推移(遷移)確率行列」と言いました。
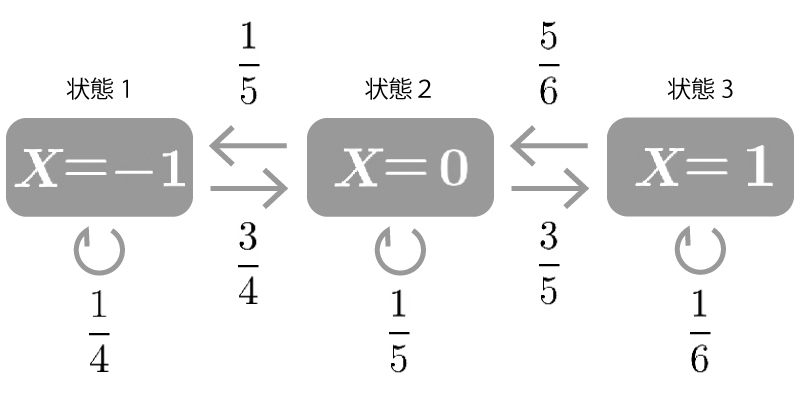
この様なマルコフ連鎖に対応する推移(遷移)確率行列$P$は以下の様になりましたね。 (参照:<マルコフ連鎖>:例1)
$$\begin{aligned} \begin{pmatrix} \displaystyle \frac{1}{4} & \displaystyle \frac{3}{4} & 0 \\[10px] \displaystyle \frac{1}{5} & \displaystyle \frac{1}{5} & \displaystyle \frac{3}{5} \\[10px] 0 & \displaystyle \frac{5}{6} & \displaystyle \frac{1}{6} \end{pmatrix} \end{aligned}$$
0-3. 定常分布
(マルコフ連鎖$\{ X_n \}$に対して、状態確率ベクトルを$\vec \pi_n$、推移(遷移)確率行列を$P$とします)
$$\begin{aligned} \vec \pi_{const} = \vec \pi_{const} P \end{aligned}$$なる$\vec \pi_{const}$が存在する時、$\vec \pi_{const}$を「定常分布」と言いました。
どの様な初期分布からスタートしようと推移を繰り返すことで、状態ベクトルは定常分布に収束します。(ただし、ある特定の条件が成立することは必要です。)
定常分布は、推移が平衡状態にある分布となります。
定常分布の具体例については<マルコフ連鎖>で確認してください。
さてマルコフ連鎖の復習をしたので、以下はMCMCの話に移りましょう。
1. なぜMCMCを用いるのか?
これまで逆関数法や受容棄却法を扱ってきましたが、これらの手法ではうまくサンプリングできない場合があります。
まず逆関数法については、分布関数の逆関数を陽に書くことができない場合には用いることができません。
また受容棄却法については、次元の大きいベクトルについてうまくサンプリングができません。
(以下説明参照)
説明. (次元の大きいベクトルについて受容棄却法ではうまくサンプリングができないことについて)
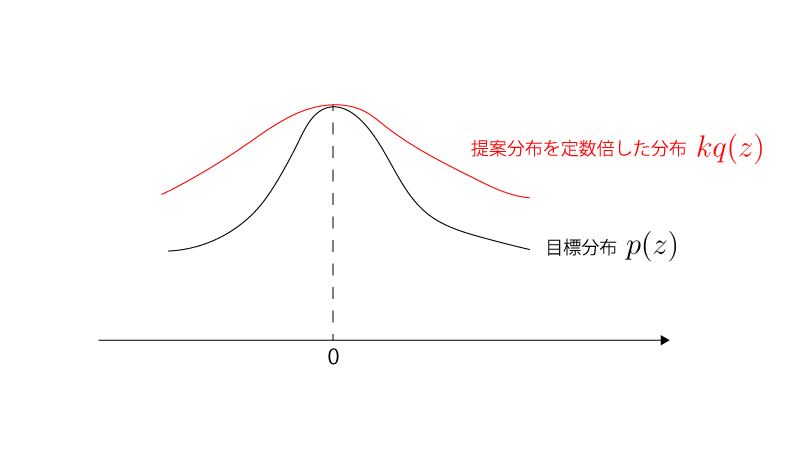
目標分布$p(\vec z)$:$\N_d(\vec 0, \sigma_p^2 I)$
提案分布$q(\vec z)$:$\N_d(\vec 0, \sigma_q^2 I)$ ($\sigma_p^2 \gt \sigma_q^2$)
とします。
$q(z),k$は、
$$\begin{aligned} k q(\vec z) \geqq p(\vec z) ~~~~~ \small{(\forall \vec z \in \mathrm{\vec R}^d)} \end{aligned}$$を満たす必要がありますが、これを満たす最小の$k$は、
$$\begin{aligned} k = \frac{p(0)}{q(0)} = (\frac{\sigma_q}{\sigma_p})^d \end{aligned}$$となりますが、この時のサンプリングの受容率は、
$$\begin{aligned} \int \frac{p(\vec z)}{k q(\vec z)} q(\vec z) d \vec z &= \frac{1}{k} \int p(\vec z) d \vec z \\ &= \frac{1}{k} \\[10px] &= (\frac{\sigma_p}{\sigma_q})^d \\[10px] &\overset{ d \to \infty}\longrightarrow 0 \end{aligned}$$となります。
(参照:C.M. ビショップ『パターン認識と機械学習』丸善出版, 2012.)
つまり、次元の大きいベクトルをサンプリングしようとした時、その受容率が0に近くなってしまい、うまく(正確には『効率的な』)サンプリングができないことになります。
まとめると、受容棄却法の様に独立に(1つずつ別個に)乱数を得るアプローチは高次元の状況で困難を生じてしまうわけです。そこで系列的($\neq$独立)にサンプリングする方法が求められますが、MCMCはその様なサンプリング法の1つです。
2. MCMCの概要
MCMCとはマルコフ性の考えに従い『1つ前に生成した乱数のみに依存して次の乱数を生成する』サンプリング法です。
Figでイメージすると下記の様になります。
Fig.
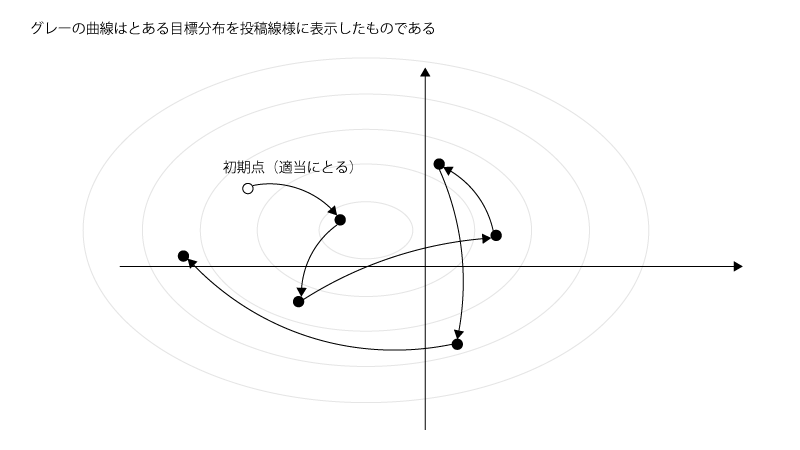
(↑初期点は適当に与えるとして、1つ前に生成した乱数のみに依存して次の乱数が生成されます)
MCMCでは、マルコフ性に従って生成される乱数が最終的に従う分布(定常分布)が、目標分布(ここから乱数を生成したいと考えていた分布)に一致する様にアルゴリズム(マルコフ性に基づく状態推移のルール)を組むことになります。
今回はMCMCの代表的アルゴリズムである、Metropolis-Hastings、Gibbs sampling、を紹介しますが、いずれも『定常分布が目標分布に一致する』様に組まれています。
これによって、十分推移を繰り返した後の乱数(例えば1000個目以降の乱数)は定常分布、つまり、ここでは目標分布に従ってるとみなせるので、それを目標分布からの乱数として採用します。
マルコフ連鎖では離散的な状態を扱いましたが、MCMCでは連続的な状態も扱います。しかしながら、離散的か連続的かは本質的な問題ではなく、あくまでその本質は『マルコフ性に基づき状態が推移していく』ということです。
1つ前の状態のみに依存して乱数が生成されていくことが本質なのですね。
ところで、例で1000個目以降の乱数を採用、つまり、999個目までの乱数を却下とありましたが、こちらについて補足して欲しいです。
はい。
なぜ999個目までの乱数を却下したかというと、「初期点の位置」による影響と、マルコフ連鎖がまだ収束してない可能性を考えてのことです。
この様に一定までの乱数は却下するのは一般的なことです。
却下される乱数の期間は『バーンイン期間(burn-in period)』と呼ばれます。
わかりました。
3. MCMCの具体的なアルゴリズム
MCMCの代表的アルゴリズムである、Metropolis-Hastings、Gibbs sampling、を紹介します。
2次元ベクトル$\vec z = (z_1, z_2)$を目標分布(定常分布とする)からサンプルするとした時の目標分布のイメージ図は以下の様になります。
Fig. (目標分布のイメージ図)
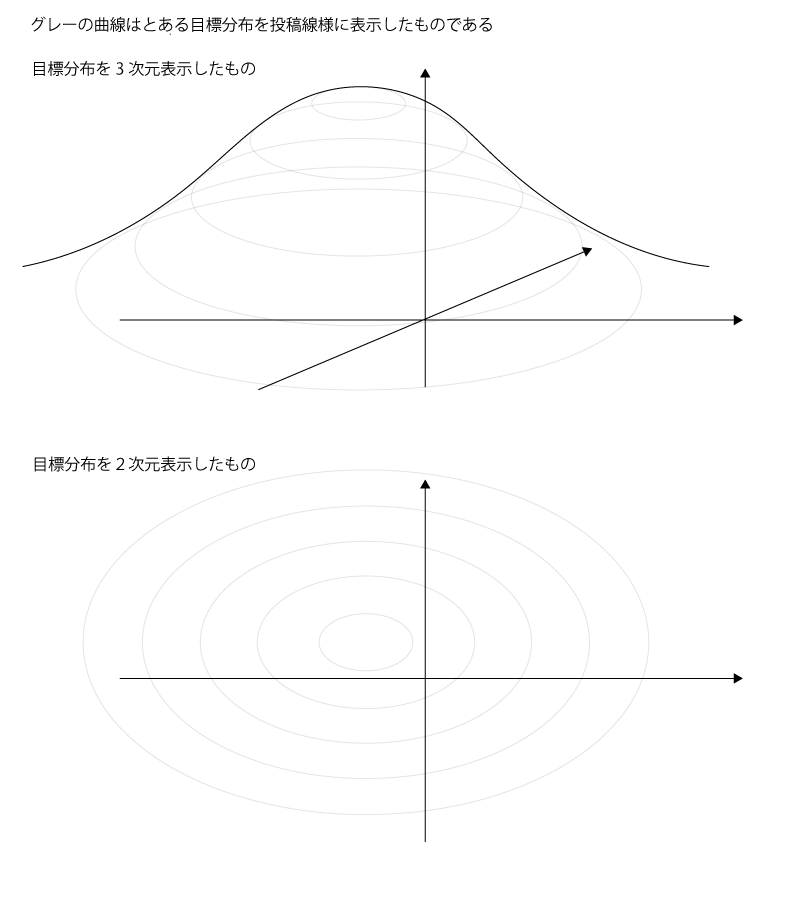
3-1. Metropolis-Hastings
Metropolis-Hastingsでは、次の点の候補をsampleするための分布$q(\vec z| \vec z^{(i)})$(これを『提案分布』といいます)、を準備します。
なお、提案分布としては正規分布、$\t$分布、一様分布などがよく使われます。
Metropolis-Hastingsのアルゴリズムは以下の様になります。
for i=0,1,…,do
$~~~~$# 提案分布$q(\vec z| \vec z^{(i)})$からサンプルする
$~~~~$sample $\vec z^* \sim q(\vec z| \vec z^{(i)})$
$~~~~$# 下記の通り$A(\vec z^*, \vec z^{(i)})$を定める
$~~~~$# ただし$p()$は目標分布を表す
$~~~~$$A(\vec z^*, \vec z^{(i)}) = \min\{ 1, \frac{p(\vec z^*) q(\vec z^{(i)} | \vec z^*)}{p(\vec z^{(i)} ) q(\vec z^* | \vec z^{(i)})} \}$
$~~~~$# 下記の通り$\vec z^{(i+1)}$を更新する
$~~~~$・$\vec z^{(i+1)}$←$\vec z^*$ with probability $A(\vec z^*, \vec z^{(i)})$
$~~~~$・$\vec z^{(i+1)}$←$\vec z^{(i)}$ otherwise (probability $1-A(\vec z^*,\vec z^{(i)})$)
$~~~~$end
最終的にiが一定以降(1000以降など)のサンプルを採用する。
この様なアルゴリズムの下では$\vec z$の定常分布は目標分布$p(\vec z)$となります。
(この証明に興味がある方は<補足. MCMC>を参照ください)
初期値$\vec z^*$からスタートして順々に更新してますね。
$A(\vec z^*, \vec z^{(i)})$なる値を定めてそれに基づく形で$\vec z^{(i+1)}$を$\vec z^{(i)}$とは別の$\vec z^*$という値に更新するか、$\vec z^{(i)}$のままとするかを決めるのですね。
その通りです。
イメージとしては下記の様になります。
Fig.
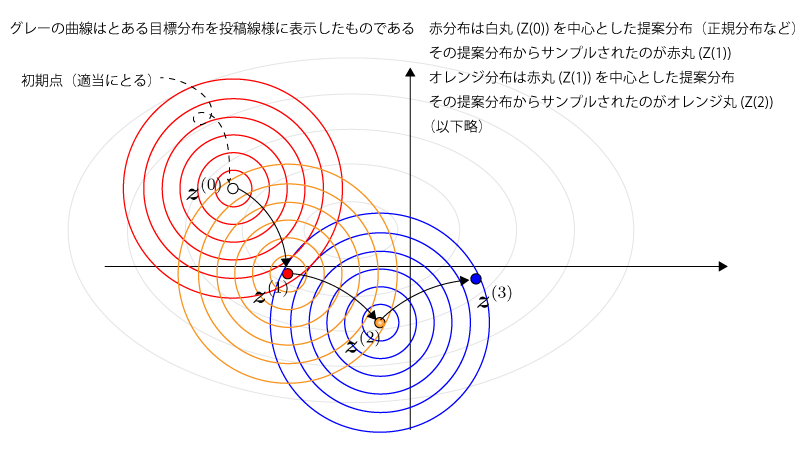
なるほど。1つ前の状態に依存した分布に基づいて次のサンプルがなされてますね。
はい。それとこのアルゴリズムにおいては正規化定数を考える必要がないことも重要です。
具体的には目標分布$p(\vec z)$と正規化定数$C$に対して、$p(\vec z) = C \tilde{p}(\vec z)$と書ける時、$\tilde{p}(\vec z)$のみわかっていればokです。
それは$A(\vec z^*, \vec z^{(i)})$の定義式において$p()$が分母・分子に含まれていて正規化定数$C$が分母・分子でキャンセルアウトされるからでしょうか?
その通りです!なお、ベイズ統計において事後分布を考える時には$\tilde{p}(\vec z)$のみわかっていることがよくありますが、このアルゴリズムを使えば問題なくサンプルを続けられます。
補足.
原点対称な分布(正規分布、$\t$分布、一様分布)$K()$に対して、提案分布$q()$を、
$$\begin{aligned} q(\vec z^{*} | \vec z^{(i)}) = K(\vec z^*-\vec z^{(i)}) \end{aligned}$$と定めることが多いです。
この時、
$$\begin{aligned} q(\vec z^{(i)} | \vec z^*) = q(\vec z^* | \vec z^{(i)}) \end{aligned}$$が成立するため、前出のアルゴリズムにおいて、
$$\begin{aligned} A(\vec z^*, \vec z^{(i)}) = \min\{ 1, \frac{p(\vec z^*)}{p(\vec z^{(i)} )} \} \end{aligned}$$となります。
よって、提案分布$q()$からランダムサンプルした$z^*$について、$p(\vec z^*) \geqq p(\vec z^{(i)})$、となれば、$A(\vec z^*,\vec z^{(i)}) = 1$、より$\vec z^{(i)}$→$\vec z^*$と必ず推移します。一方で、$p(\vec z^*) \lt p(\vec z^{(i)})$、となれば、$A(\vec z^*, \vec z^{(i)}) = \frac{p(\vec z^*)}{p(\vec z^{(i)} )}$、より$\vec z^{(i)}$→$\vec z^*$と必ず推移するわけではありません。(確率$\frac{p(\vec z^*)}{p(\vec z^{(i)} )} (\leqq 1)$で推移する)
言い換えると、目標分布$p()$において確率が高い点をより取りたがり、目標分布$p()$において確率が低い点をより取りたがらないことになります。その結果、ゆくゆくは乱数が目標分布$p()$からサンプリングされることになります。
3-2. Gibbs sampling
Gibbs samplingでは提案分布を準備する必要はなく、目標分布を直接用います。
Gibbs samplingのアルゴリズムは以下の様になります。
for i=0,1,…,do
$~~~~$# Gibbs samplingではベクトルを構成する要素を1つずつ更新する
$~~~~$# $\vec z^{(i)} = (z_1^{(i)},\cdots,z_K^{(i)})$、と$K$要素からなるものとする
$~~~~$# $p()$は目標分布を表す
$~~~~$sample $z_1^{(i+1)} \sim p(z_1 | z_2^{(i)},\cdots,z_K^{(i)})$
$~~~~$sample $z_2^{(i+1)} \sim p(z_2 | z_1^{(\color{red}{i+1})},z_3^{(i)},\cdots,z_K^{(i)})$
$~~~~$・・・(以下同様)・・・
$~~~~$sample $z_K^{(i+1)} \sim p(z_K | z_1^{(\color{red}{i+1})},\cdots,z_{K-1}^{(\color{red}{i+1})})$
$~~~~$# 上記プロセスにおいては、『目標分布$p()$において、ベクトル$\vec z$を構成する要素の1つは、残りの要素が条件づけられていればsample可能(*)』という条件下で話を進めています
$~~~~$end
最終的にiが一定以降(1000以降など)のサンプルを採用する。
この様なアルゴリズムの下では$\vec z$の定常分布は目標分布$p(\vec z)$となります。
(この証明に興味がある方は<補足. MCMC>を参照ください)
Gibbs samplingは、Metropolist-Hastingの様にある確率で更新するか否かを決めるというアルゴリズムではなく、必ず値は更新されるアルゴリズムとなっていますね。
その通りです。
Metropolis-Hastingsと比較してGibbs samplingがよいところは、提案分布をわざわざ準備する必要がないという点です。
一方で悪いところは、上記(*)の条件が成立する時にしか使えないという点です。
なるほどです。
ところで、Gibbs samplingは必ず値が更新されるので、Metroplis-Hastingsよりも効率が良いように思いますがいかがでしょうか?
その様に思われるかもしれませんが、実のところは必ずしもそういうわけではありません。
つまり、Metropolis-Hastingsにおいてよい提案分布を準備してあげた時、Gibbs samplingよりも効率的にsamplingが進むこともあるというわけです。
最後になりますが、Gibbs samplingでsamplingが進むプロセスのFigを下記に提示します。
Fig.
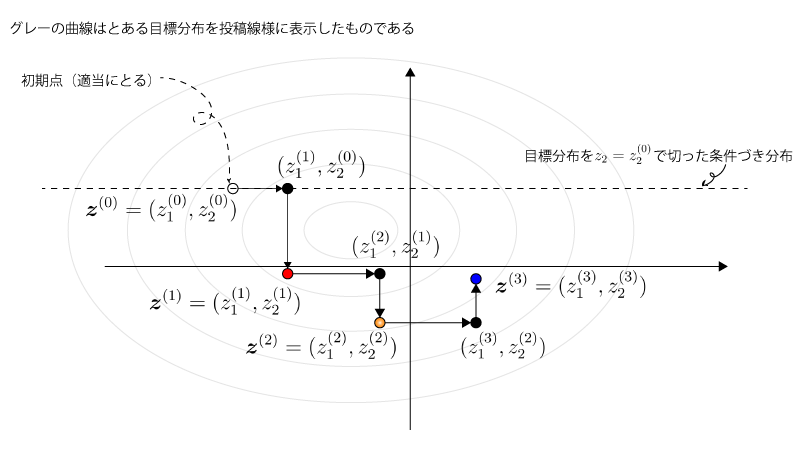
3-3. Metropolis-HastingsとGibbs samplingの違いのまとめ
以下Metropolis-HastingsとGibbs samplingの違いを整理しておきます。
| Metropolis-Hastings | Gibbs sampling | |
| 提案分布は必要か? | 必要(提案分布によってsampling効率が変化) | 不要 |
| 値は毎回必ず更新されるか? | されない(一定確率で更新される) | される |
| $\vec z = (z_1, z_2)$のsamplingはどう推移するか? | $\vec z = (z_1, z_2)$→$\vec z’ = (z’_1, z’_2)$と一気に推移する | $\vec z = (z_1, z_2)$→$(z’_1, z_2)$→$\vec z’ = (z’_1, z’_2)$と段階的に推移する |
| 使える状況 | 分布の比($\frac{p(\vec z’)}{p(\vec z)}$)がわかる | 完全条件付き分布からsampleできる |
完全条件付き分布とは$\vec z = (z_1,\cdots,z_K)$とした時、$p(z_1 | z_2,\cdots,z_K)$、の様にある1つの要素以外を条件付けた分布となります。Gibbs samplingではその様な完全条件付き分布からsampleできる必要があり、Metropolis-Hastingsでは分布の比がわかるだけでよいのと比べると、使用できる場面は限定的となります。
なるほど、Metropolis-Hastingsの方が汎用的なのですね。
ただ、Metropolis-Hastingsでは提案分布を準備する必要があるため、手間的にはMetropolis-Hastingsの方がGibbs samplingよりも優れているという一般化はできませんよね?
そうですね。どちらが必ず優れてると言えるものではありません。また、今回はMCMCの代表的な手法の2つを紹介しましたが、例えばMetropolis-Hastingsをより効率化することを目指したHamiltonian Monte Carloといったよく使われる手法もあります。ここでMCMCの基本を押さえて適宜レパートリーを増やしていけばよいかと思います。
4. MCMCでやっていることのまとめ
ここまでMCMCの具体的アルゴリズムを扱ってきましたが、結局のところどういったことをしていたのかをまとめます。
目標:
特定の目標分布$p()$からsampleする。
MCMCによる解決策:
特定の目標分布$p()$を定常分布に持つようなマルコフ連鎖を構成して、十分長い時間シミュレーションする。マルコフ連鎖は定常分布に近づくので(ほぼ)特定の目標分布$p()$からのサンプリングができる。
適切なマルコフ連鎖の構成の方法:
マルコフ連鎖は次の状態への推移確率$R(\vec z^{(i+1)}\mid \vec z^{(i)})$で特徴づけられる。この$R$をマルコフ連鎖の定常分布が特定の目標分布$p()$に一致するように定めたい。
この条件を数式で書くと、
$$\begin{aligned} p(\vec z^{(i+1)}) = \int R(\vec z^{(i+1)} \mid \vec z^{(i)}) p(\vec z^{(i)})d \vec z^{(i)} \end{aligned}$$
この条件を満たす$R$の構成方法として、Metropolis-HastingsやGibbs Samplingがありました。
最後の式は$p()$が定常分布であることの定義式です。なかなかこの式の意味を直感的に理解することは難しいので説明してみます。まず、$\vec z^{(i+1)}$を$\vec z^{(i)}$と推移確率$R(\vec z^{(i+1)}\mid \vec z^{(i)})$によって得るとします。一般に『($a,b$の同時分布)=($a$の分布)$\times$($a$を条件づけた時の$b$の条件付き分布)』であることから、$(\vec z^{(i)}, \vec z^{(i+1)})$の同時分布は$p(\vec z^{(i)}) R(\vec z^{(i+1)} \mid \vec z^{(i)})$となり、上式右辺の被積分項となります。上式右辺ではこれを$\vec z^{(i)}$について積分してるので、右辺は$\vec z^{(i+1)}$の従う分布を表します。それが左辺、つまり、$p(\vec z^{(i+1)})$に一致します。以上より、$\vec z^{(i)}, \vec z^{(i+1)}$いずれの従う分布も$p()$となるわけです。
まとめ.
- MCMCとはマルコフ性を利用した系列的なサンプリング法である。
- MCMCの代表的アルゴリズムとしてMetropolis-HastingsとGibbs samplingがあり、サンプリング方式や適用条件は異なるが、「定常分布が目標分布に一致する様にアルゴリズムが組まれている」という点で共通している。








