$ \gdef \vec#1{\boldsymbol{#1}} \gdef \rank {\mathrm{rank}} \gdef \det {\mathrm{det}}$
今回はマルコフ連鎖を扱いますが、そのためにその元となる性質「マルコフ性」をまず確認します。
「マルコフ性」とはどういった性質でしょうか?
確率変数列$\{ X_n \} ~{\small (n=0, \cdots)}$に対して、
$Pr\{ X_{n+1} | X_n=x_n, \ldots, X_0=x_0 \} = Pr\{ X_{n+1} | X_n=x_n \}$、 なる性質を「マルコフ性」と言います。
つまり、『$X_0, \ldots, X_n$を条件づけた下での$X_{n+1}$の分布が、$X_n$のみを条件づけた$X_{n+1}$の分布と等しい』という性質ですね。
その通りです。
さらにシンプルに言い換えてみると、『直前の状態のみから次の状態が決まる』という性質です。
シンプルなイメージも大切にしてください!
1. マルコフ性とマルコフ連鎖
(確率変数列$\{ X_n \} ~{\small(n=0, \ldots)}$のことを「確率過程」とも言います)
確率変数列(確率過程)$\{ X_n \} ~{ \small (n=0, \ldots)}$に対して、
$$ \begin{aligned} \boldsymbol{Pr\{ X_{n+1}| X_n=x_n, \ldots, X_0=x_0 \} = Pr\{ X_{n+1}| X_n=x_n\}} \end{aligned} $$なる性質を「マルコフ性」と言います。
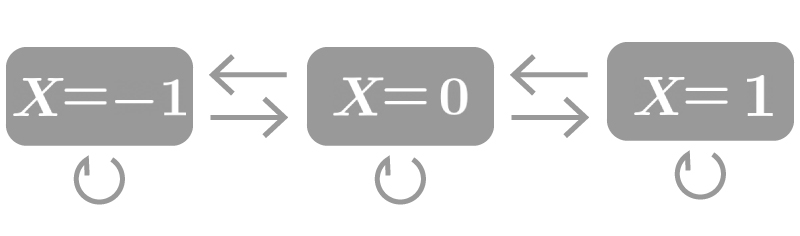
また、マルコフ性をもつ確率変数列(確率過程)$\{ X_n \}~{ \small (n=0, \ldots)}$のとりうる状態が離散的である時(例. Fig1)、$\{ X_n \}$を「マルコフ連鎖」と言います。
Fig1.
2. 状態確率ベクトルと推移(遷移)確率行列
マルコフ連鎖における状態空間は離散的であるため、時点$n$において各状態(状態$1,…,k$)にいる確率をまとめたものをベクトル
$$\begin{aligned} \vec \pi_n = (\pi_{n,1}, \ldots, \pi_{n,k}) \end{aligned} $$(ただし、$\sum_{l=1}^k \pi_{n,l} = 1$)
と表すことができ、これを「状態確率ベクトル」と言います。
また、$$ \begin{aligned} \vec \pi_{n+1} = \vec \pi_n P ~~~~~\mathrm{(A)} \end{aligned}$$ と時点が1ずれた状態確率ベクトルを関係づける行列$P$を「推移(遷移)確率行列」と言います。
- 一般には推移確率行列$P$は時点$n$に依存して変化しうるので$P_n$と書かれるべきですが、$\mathrm{(A)}$では推移確率行列が時点$n$に依存しない場合を扱いました。
- 「$\vec \pi_{n+1} = P \vec \pi_n$」と書くべきではないかと思った方もいるかと思いますが、状態確率ベクトルは慣習的に横ベクトルで記載されるために、「$\vec \pi_{n+1} = \vec \pi_n P$」の様に一般に書かれます。
例1.
時点$0$で$X=0$をとり、時点$n$で$X=-1, 0, 1$をとる確率をそれぞれ$a_n, b_n, c_n$とする。 ただし、$X$は$-1, 0, 1$のいずれかの値をとるため、$a_n + b_n + c_n = 1$が成立する。 この時、以下の図の様に推移する場合を考える。
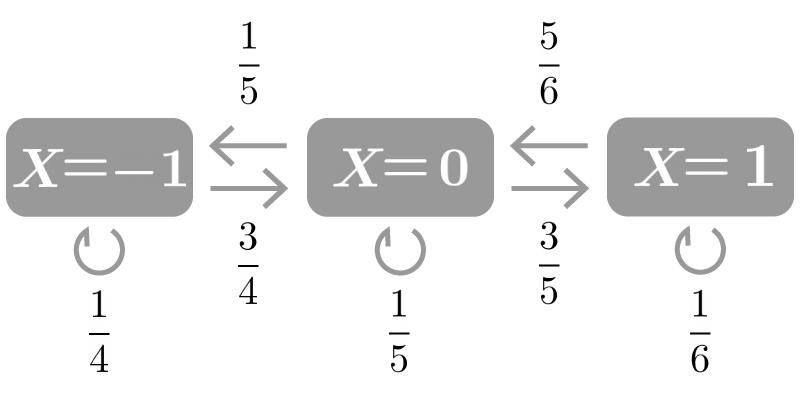
すると、$$ \begin{aligned} a_{n+1} &= \frac{1}{4} a_n + \frac{1}{5} b_n \\ b_{n+1} &= \frac{3}{4} a_n + \frac{1}{5} b_n + \frac{5}{6} c_n \\ c_{n+1} &= ~~~~~~~~~~~ \frac{3}{5} b_n + \frac{1}{6} c_n \end{aligned}$$ が成立し、これを行列形式で書くと、$$ \begin{aligned} (a_{n+1}, b_{n+1}, c_{n+1}) = (a_n, b_n, c_n) \begin{pmatrix} \displaystyle \frac{1}{4} & \displaystyle \frac{3}{4} & 0 \\[10px] \displaystyle \frac{1}{5} & \displaystyle \frac{1}{5} & \displaystyle \frac{3}{5} \\[10px] 0 & \displaystyle \frac{5}{6} & \displaystyle \frac{1}{6} \end{pmatrix} \end{aligned}$$ となる。
この時、$(a_{n+1}, b_{n+1}, c_{n+1}), (a_n, b_n, c_n)$が状態確率ベクトルに相当し、$$ \begin{aligned} \begin{pmatrix} \displaystyle \frac{1}{4} & \displaystyle \frac{3}{4} & 0 \\[10px] \displaystyle \frac{1}{5} & \displaystyle \frac{1}{5} & \displaystyle \frac{3}{5} \\[10px] 0 & \displaystyle \frac{5}{6} & \displaystyle \frac{1}{6} \end{pmatrix} \end{aligned}$$が推移確率行列に相当する。
3. 定常分布と極限分布
(マルコフ連鎖$\{ X_n \}$に対して、状態確率ベクトルを$\vec \pi_n$、推移確率行列を$P$とします)
(定常分布の定義)
$$ \begin{aligned} \vec \pi_{const} = \vec \pi_{const} P \end{aligned} $$なる$\vec \pi_{const}$が存在する時、$\vec \pi_{const}$を「定常分布」と言います。
(極限分布の定義)
$\displaystyle \lim_{n \to \infty} \vec \pi_n$が存在する時、$\displaystyle \lim_{n \to \infty} \vec \pi_n$を「極限分布」と言います。
- さきほどまで「状態確率ベクトル」という名称を用いていた部分が「分布」という名称に変わりましたが、「定常分布」=「定常状態確率ベクトル」、「極限分布」=「極限状態確率ベクトル」と考えてください。
4. 定常分布と極限分布の関係
定常分布と極限分布については、 $$ \begin{aligned} \boldsymbol{ 「\vec \pi {\small は極限分布}」 \Rightarrow 「\vec \pi \small{は定常分布}」} \end{aligned}$$ は成立しますが、その逆は必ずしも成立しません。
($\boldsymbol{ 「\vec \pi {\small は極限分布}」 \Rightarrow 「\vec \pi \small{は定常分布}」}$の証明)
極限分布が存在する時、それを$\vec \pi_{\infty} = \displaystyle \lim_{n \to \infty} \vec \pi_n$とする。
$\vec \pi_{n+1} = \vec \pi_n P$の両辺について$n \to \infty$とすると、$$ \begin{aligned} \lim_{n \to \infty} \vec \pi_{n+1} &= \lim_{n \to \infty} (\vec \pi_n P) \\ &= (\lim_{n \to \infty} \vec \pi_n) P \\ &{\scriptsize (線形性より)} \end{aligned}$$
よって、$\vec \pi_{\infty} = \vec \pi_{\infty} P$となり、$\vec \pi_{\infty}$は定常分布となる。
($\boldsymbol{ 「\vec \pi {\small は定常分布}」 \Rightarrow 「\vec \pi \small{は極限分布}」}$の反例)
以下の様なマルコフ連鎖を考える。
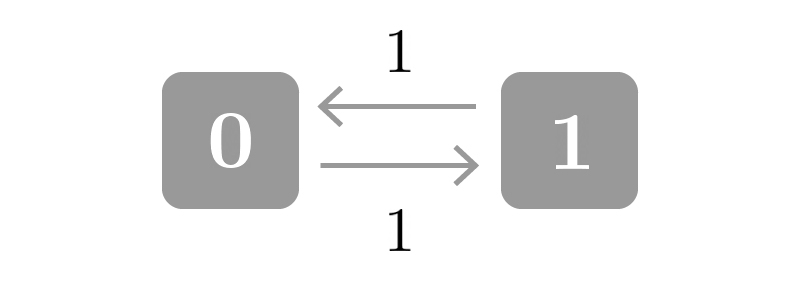
時点$0$で$X_t = 0$をとるとした時、$$ \begin{aligned} X_t = \begin{cases} 0 ~~ (t:{\small 奇数}) \\ 1 ~~ (t:{\small 偶数}) \end{cases} \end{aligned}$$となるため、$\displaystyle \lim_{n \to \infty} \vec \pi_n$は存在しない。
ところで、このマルコフ連鎖は$$ \begin{aligned} \vec \pi_{n+1} = \vec \pi_n \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \end{aligned} $$と書けるが、
$\vec \pi_{const} = (a_{const}, b_{const})$として、
$$ \begin{alignat}{2} \notag &&\vec \pi_{const} &= \vec \pi_{const} \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \\[10px] \notag &\Rightarrow& (a_{const}, b_{const}) &= (a_{const}, b_{const}) \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \\ \notag &&&= (b_{const}, a_{const}) \\[10px] \notag &\Rightarrow & a_{const} &= b_{const} \end{alignat}$$ となり、$a_{const} + b_{const} = 1$であることも考慮すると、$$ \begin{aligned} \vec \pi_{const} = (a_{const}, b_{const}) = (\frac{1}{2}, \frac{1}{2}) \end{aligned}$$ となり、$\vec \pi_{const}$は存在する。
例題1.
状態確率ベクトル$\vec \pi_n$、推移確率行列$P$が以下の通りであるマルコフ連鎖を考える。
$$ \begin{aligned} \vec \pi_n &= (a_n, b_n, c_n) \\ P &= \begin{pmatrix} \displaystyle \frac{1}{2} & \displaystyle \frac{1}{2} & 0 \\[10px] 0 & \displaystyle \frac{1}{2} & \displaystyle \frac{1}{2} \\[10px] 0 & \displaystyle \frac{1}{3} & \displaystyle \frac{2}{3} \end{pmatrix} \end{aligned}$$
この時、定常分布$\vec \pi_{const} (= (a_{const}, b_{const}, c_{const}))$を求めよ。
解答.
定常分布$\vec \pi_{const} (= (a_{const}, b_{const}, c_{const}))$が存在するとした時、$$ \begin{aligned} \vec \pi_{const} = \vec \pi_{const} P \\ {\scriptsize (定常分布の定義より)} \end{aligned}$$ $$\begin{aligned} \Rightarrow (a_{const}, b_{const}, c_{const}) &= (a_{const}, b_{const}, c_{const}) \begin{pmatrix} \displaystyle \frac{1}{2} & \displaystyle \frac{1}{2} & 0 \\[10px] 0 & \displaystyle \frac{1}{2} & \displaystyle \frac{1}{2} \\[10px] 0 & \displaystyle \frac{1}{3} & \displaystyle \frac{2}{3} \end{pmatrix} \\ &= (\frac{1}{2} a_{const}, ~\frac{1}{2} a_{const} + \frac{1}{2} b_{const} + \frac{1}{3} c_{const}, ~\frac{1}{2} b_{const} + \frac{2}{3} c_{const}) \end{aligned}$$
これを$a_{const} + b_{const} + c_{const} = 1$とあわせて解くと、 $$ \begin{aligned} (a_{const}, b_{const}, c_{const}) &= (0, \frac{2}{5}, \frac{3}{5}) \\ \Rightarrow \vec \pi_{const} &= (0, \frac{2}{5}, \frac{3}{5}) \end{aligned}$$
5. 一般の$\vec \pi_nの求め方$
ここでは、状態確率ベクトルの初期値$\vec \pi_0$、推移確率行列$P$であるマルコフ連鎖に対して、$\vec \pi_n$を求める方法を考えます。
まず、$$ \begin{aligned} \vec \pi_{n+1} &= \vec \pi_n P \\ &= (\vec \pi_{n-1} P) P \\ &= \vec \pi_{n-1} P^2 \end{aligned}$$なので、これをくり返すと$$ \begin{aligned} \vec \pi_n = \vec \pi_0 P^n \end{aligned}$$となります。
即ち、$\vec \pi_n$を求めるためには$P^n$を求めればよいことになり、結局は『行列のn乗計算』に帰着されます。
『行列のn乗計算』は以下のプロセスに従って進められますが*、 わからない方は<行列のn乗計算の方法>を参照ください。 (*:ただし、ここでは対角化可能な場合を扱います)
1.$P$の固有値・固有ベクトルの計算
2.固有値をならべた『変換行列$Q$』の作成
3.変換行列$Q$の逆行列$Q^{-1}$の計算
4.対角行列$Q^{-1}PQ$の作成
5.$(Q^{-1}PQ)^n$の計算
以下の例題を通じて一般の$\vec \pi_n$の求め方を確認してください。
例題2.
状態確率ベクトル$\vec \pi_n$、推移確率行列$P$が以下の通りであるマルコフ連鎖を考える。
$$ \begin{aligned} \vec \pi_n &= (a_n, b_n, c_n) \\ P &= \begin{pmatrix} \displaystyle \frac{1}{2} & \displaystyle \frac{1}{2} & 0 \\[10px] 0 & \displaystyle \frac{1}{2} & \displaystyle \frac{1}{2} \\[10px] 0 & \displaystyle \frac{1}{3} & \displaystyle \frac{2}{3} \end{pmatrix} \end{aligned}$$状態確率ベクトルの初期値$\vec \pi_0$を$\vec \pi_0 = (a_0, b_0, c_0)$とする時、$\vec \pi_n$を求めよ。
解答.
(1.$P$の固有値・固有ベクトルの計算)
$P$の固有方程式は$$ \begin{aligned} \det (P – \lambda E) = 0 \end{aligned} $$ $$ \begin{aligned} \Rightarrow \det \begin{pmatrix} (\displaystyle \frac{1}{2} – {\lambda}) & \displaystyle \frac{1}{2} & 0 \\[10px] 0 & (\displaystyle \frac{1}{2} – \lambda) & \displaystyle \frac{1}{2} \\[10px] 0 & \displaystyle \frac{1}{3} & (\displaystyle \frac{2}{3} – \lambda) \end{pmatrix} = 0 \end{aligned}$$ $$ \begin{aligned} &\Rightarrow (\lambda – \displaystyle \frac{1}{6})(\lambda – \displaystyle \frac{1}{2})(\lambda – 1) = 0 \\ &{\scriptsize (途中計算は省略)} \end{aligned}$$
よって、固有値$\lambda = \displaystyle \frac{1}{6}, \displaystyle \frac{1}{2}, 1$と求められる。
固有値$\lambda = \displaystyle \frac{1}{6}$に対応する固有ベクトルの1つを$\vec x_1$とすると、$$ \begin{aligned} \begin{pmatrix} (\displaystyle \frac{1}{2} – \displaystyle \frac{1}{6}) & \displaystyle \frac{1}{2} & 0 \\[10px] 0 & (\displaystyle \frac{1}{2} – \displaystyle \frac{1}{6}) & \displaystyle \frac{1}{2} \\[10px] 0 & \displaystyle \frac{1}{3} & (\displaystyle \frac{2}{3} – \displaystyle \frac{1}{6}) \end{pmatrix} \vec x_1 = \vec 0 \end{aligned}$$ $$\begin{aligned} &\Rightarrow \vec x_1 = \begin{pmatrix} -9 \\ 6 \\ -4 \end{pmatrix} \\ &{\scriptsize (注意:この定数倍であればよいです)} \end{aligned}$$
同様に、固有値$\lambda = \displaystyle \frac{1}{2}, 1$に対応する固有ベクトルの1つをそれぞれ$\vec x_2, \vec x_3$とすると、$$ \begin{aligned} \vec x_2 &= \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \\[10px] \vec x_3 &= \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \end{aligned}$$ となる。
(2.固有値をならべた『変換行列$Q$』の作成)
ここで、変換行列$Q$を $$ \begin{aligned} Q &= (\vec x_1 \vec x_2 \vec x_3) \\[10px] &= \begin{pmatrix} -9 & 1 & 1 \\ 6 & 0 & 1\\ -4 & 0 & 1 \end{pmatrix} \end{aligned}$$ とする。
(3.変換行列$Q$の逆行列$Q^{-1}$の計算)
$Q$の逆行列$Q^{-1}$を以下の通りはき出し法で求める。
$$ \begin{aligned} &\left( \begin{array}{ccc|ccc} -9 & 1 & 1 & 1 & 0 & 0 \\ 6 & 0 & 1 & 0 & 1 & 0 \\ -4 & 0 & 1 & 0 & 0 & 1 \end{array} \right) \\[20px] \Rightarrow &\left( \begin{array}{ccc|ccc} -36 & 4 & 4 & 4 & 0 & 0 \\ 36 & 0 & 6 & 0 & 6 & 0 \\ -36 & 0 & 9 & 0 & 0 & 9 \end{array} \right) \\[20px] \Rightarrow &\left( \begin{array}{ccc|ccc} 0 & 4 & 10 & 4 & 6 & 0 \\ 36 & 0 & 6 & 0 & 6 & 0 \\ 0 & 0 & 15 & 0 & 6 & 9 \end{array} \right) \\[20px] \Rightarrow &\left( \begin{array}{ccc|ccc} 0 & 12 & 30 & 12 & 18 & 0 \\ 180 & 0 & 30 & 0 & 30 & 0 \\ 0 & 0 & 30 & 0 & 12 & 18 \end{array} \right) \\[20px] \Rightarrow &\left( \begin{array}{ccc|ccc} 0 & 12 & 0 & 12 & 6 & -18 \\ 180 & 0 & 0 & 0 & 18 & -18 \\ 0 & 0 & 30 & 0 & 12 & 18 \end{array} \right) \\[20px] \Rightarrow &\left( \begin{array}{ccc|ccc} 0 & 1 & 0 & 1 & \displaystyle \frac{1}{2} & -\displaystyle \frac{3}{2} \\[10px] 1 & 0 & 0 & 0 & \displaystyle \frac{1}{10} & – \displaystyle \frac{1}{10} \\[10px] 0 & 0 & 1 & 0 & \displaystyle \frac{2}{5} & \displaystyle \frac{3}{5} \end{array} \right) \\[20px] \Rightarrow &\left( \begin{array}{ccc|ccc} 1 & 0 & 0 & 0 & \displaystyle \frac{1}{10} & – \displaystyle \frac{1}{10} \\[10px] 0 & 1 & 0 & 1 & \displaystyle \frac{1}{2} & – \displaystyle \frac{3}{2} \\[10px] 0 & 0 & 1 & 0 & \displaystyle \frac{2}{5} & \displaystyle \frac{3}{5} \end{array} \right) \end{aligned}$$
よって、$$ \begin{aligned} Q^{-1} = \begin{pmatrix} 0 & \displaystyle \frac{1}{10} & – \displaystyle \frac{1}{10} \\[10px] 1 & \displaystyle \frac{1}{2} & – \displaystyle \frac{3}{2}\\[10px] 0 & \displaystyle \frac{2}{5} & \displaystyle \frac{3}{5} \end{pmatrix} \end{aligned}$$
(4.対角行列$Q^{-1}PQ$の作成)
$$ \begin{aligned} Q^{-1}PQ &= \begin{pmatrix} 0 & \displaystyle \frac{1}{10} & – \displaystyle \frac{1}{10} \\[10px] 1 & \displaystyle \frac{1}{2} & – \displaystyle \frac{3}{2} \\[10px] 0 & \displaystyle \frac{2}{5} & \displaystyle \frac{3}{5} \end{pmatrix} \begin{pmatrix} \displaystyle \frac{1}{2} & \displaystyle \frac{1}{2} & 0 \\[10px] 0 & \displaystyle \frac{1}{2} & \displaystyle \frac{1}{2} \\[10px] 0 & \displaystyle \frac{1}{3} & \displaystyle \frac{2}{3} \end{pmatrix} \begin{pmatrix} -9 & 1 & 1 \\ 6 & 0 & 1 \\ -4 & 0 & 1 \end{pmatrix} \\[10px] &= \begin{pmatrix} \displaystyle \frac{1}{6} & 0 & 0 \\[10px] 0 & \displaystyle \frac{1}{2} & 0 \\[10px] 0 & 0 & 1 \end{pmatrix} \end{aligned}$$
(5.$(Q^{-1}PQ)^n$の計算)
$$\begin{aligned} (Q^{-1}PQ)^n &= Q^{-1}P^nQ = \begin{pmatrix} (\displaystyle \frac{1}{6})^n & 0 & 0 \\[10px] 0 & (\displaystyle \frac{1}{2})^n & 0 \\[10px] 0 & 0 & 1 \end{pmatrix} \end{aligned}$$ $$ \begin{aligned} \Rightarrow P^n &= Q \begin{pmatrix} (\displaystyle \frac{1}{6})^n & 0 & 0 \\[10px] 0 & (\displaystyle \frac{1}{2})^n & 0 \\[10px] 0 & 0 & 1 \end{pmatrix} Q^{-1}\\[10px] &= \begin{pmatrix} -9 & 1 & 1 \\ 6 & 0 & 1\\ -4 & 0 & 1 \end{pmatrix} \begin{pmatrix} (\displaystyle \frac{1}{6})^n & 0 & 0 \\[10px] 0 & (\displaystyle \frac{1}{2})^n & 0 \\[10px] 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 0 & \displaystyle \frac{1}{10} & – \displaystyle \frac{1}{10} \\[10px] 1 & \displaystyle \frac{1}{2} & – \displaystyle \frac{3}{2}\\[10px] 0 & \displaystyle \frac{2}{5} & \displaystyle \frac{3}{5} \end{pmatrix} \\[10px] &= \begin{pmatrix} (\displaystyle \frac{1}{2})^n & \left \{ – \displaystyle \frac{9}{10} (\displaystyle \frac{1}{6})^n + \displaystyle \frac{1}{2}(\displaystyle \frac{1}{2})^n + \displaystyle \frac{2}{5} \right\} & \left\{ \displaystyle \frac{9}{10} (\displaystyle \frac{1}{6})^n – \displaystyle \frac{3}{2}(\displaystyle \frac{1}{2})^n + \displaystyle \frac{3}{5} \right\} \\[10px] 0 & \left \{ \displaystyle \frac{6}{10} (\displaystyle \frac{1}{6})^n + \displaystyle \frac{2}{5} \right \} & \left \{ – \displaystyle \frac{6}{10} (\displaystyle \frac{1}{6})^n + \displaystyle \frac{3}{5} \right \} \\[10px] 0 & \left \{ -\displaystyle \frac{4}{10} (\displaystyle \frac{1}{6})^n + \displaystyle \frac{2}{5} \right \} & \left \{ \displaystyle \frac{4}{10} (\displaystyle \frac{1}{6})^n + \displaystyle \frac{3}{5} \right \} \end{pmatrix} \end{aligned}$$
この$P^n$を用いて、$$\begin{aligned} \vec \pi_n &= \vec \pi_0 P^n \\ &= (a_0, b_0, c_0) P^n \end{aligned}$$となる。
- この結果より極限分布$\displaystyle \lim_{n \to \infty} \vec \pi_n$を考えると、$$ \begin{aligned} \lim_{n \to \infty} \vec \pi_n &= \lim_{n \to \infty}(\vec \pi_0 P^n) \\ &= \vec \pi_0 (\lim_{n \to \infty}P^n) \\ &{\scriptsize (線形性より)}\\[10px] &= (a_0, b_0, c_0) \begin{pmatrix} 0 & \displaystyle \frac{2}{5} & \displaystyle \frac{3}{5} \\[10px] 0 & \displaystyle \frac{2}{5} & \displaystyle \frac{3}{5} \\[10px] 0 & \displaystyle \frac{2}{5} & \displaystyle \frac{3}{5} \end{pmatrix} \\ &= \begin{pmatrix} 0 & \displaystyle \frac{2}{5}(a_0 + b_0 + c_0) & \displaystyle \frac{3}{5}(a_0 + b_0 + c_0) \end{pmatrix} \\ &= \begin{pmatrix} 0 & \displaystyle \frac{2}{5} & \displaystyle \frac{3}{5} \end{pmatrix} \\ &\scriptsize{(a_0 + b_0 + c_0 = 1より)} \end{aligned}$$ となります。
この結果と、$\boldsymbol{ 「\vec \pi {\small は極限分布}」 \Rightarrow 「\vec \pi \small{は定常分布}」}$より、$\begin{pmatrix} 0 & \displaystyle \frac{2}{5} & \displaystyle \frac{3}{5} \end{pmatrix}$は定常分布となります。 ところで、例題2の設定は例題1のそれと同じであり、定常分布の結果が同じになっていることを確認してください。
まとめ.
- 『直前の状態のみから次の状態が決まる」』いう性質を「マルコフ性」と言い、マルコフ性をもつ離散的な確率過程を「マルコフ連鎖」と言う。
- $「\vec \pi{\small は極限分布}」 \Rightarrow 「\vec \pi \small{は定常分布}」$は成立するが、その逆は必ずしも成立しない。
- マルコフ連鎖における状態確率ベクトル$\vec \pi_n$の計算は、推移確率行列$P$の$n$乗計算に帰着される。