$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}} \\ \gdef \indep {\mathop{\perp\!\!\!\!\perp}} \\ \gdef \tr {\mathrm{tr}}$
ここではMCMCの各アルゴリズム(Metropolist-Hastings, Gibbs sampling)において、定常分布が、実際に目的としている目標分布$p()$に一致していることを示します。
1. Metropolis-Hastings
1-1. 準備(詳細釣り合い条件と定常分布の一般論)
分布$p(\vec z)$とマルコフ連鎖の推移確率に対して、適当な2つの点$\vec z, \vec z’$における推移が釣り合ってるものとします。
それを式・Figで表すと下記の様になります。
$$\begin{aligned} p(\vec z) \cdot R(\vec z’ | \vec z) = p(\vec z’) \cdot R(\vec z | \vec z’) \end{aligned}$$
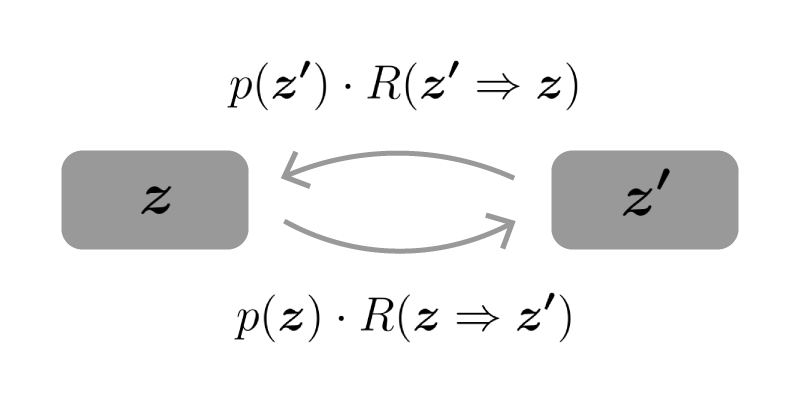
この様な推移の釣り合いが任意の2点の間について成立している時、見かけ上分布は変化していない様に見え、すなわちそれは定常分布になっていることとなります。
「推移の釣り合いが任意の2点の間について成立している」ことを『詳細釣り合い条件が成立している』と表現します。
$p(\vec z)$に対して詳細釣り合い条件が成立している時、$p(\vec z)$が定常分布になっていることは下記の様に証明もできます。
(証明)
$\vec z$から$\vec z’$への推移確率を表す分布を$R(\vec z’ | \vec z)$として、
$$\begin{aligned} p(\vec z’) = \int p(\vec z) \cdot R(\vec z’ | \vec z) d \vec z \end{aligned}$$が成立することを示せれば$p(\vec z)$が定常分布であることを示したことになるので、以下それを示す。
証明の途中で失礼します。
上式は連続分布における定常分布の定義式です。
<マルコフ連鎖>では、$\vec \pi = \vec \pi P$($\vec \pi$:状態確率ベクトル、$P$:推移確率行列)が成立する時、$\vec \pi$を定常分布と言いました。
上式はこの式を連続verにしたに過ぎません。
$$\begin{aligned} \underbrace{p(\vec z’)}_{\vec \piに相当} = \int \underbrace{p(\vec z)}_{\vec \piに相当} \cdot \underbrace{R(\vec z’ | \vec z)}_{Pに相当} d \vec z \end{aligned}$$
$$\begin{aligned} \mathrm{(上式右辺)} &= \int p(\vec z’) \cdot R(\vec z | \vec z’) d \vec z \\ &{\scriptsize(詳細釣り合い条件の式より)} \\[10px] &= p(\vec z’) \int R(\vec z | \vec z’) d \vec z \\ &{\scriptsize(p(\vec z’)は\vec zと無関係なので\intの外に出せる)} \\[10px] &= p(\vec z’) \\ &{\scriptsize(\int部分は1である)} \end{aligned}$$
1-2. Metropolis-Hastingsにおいて目標分布が定常分布となることの証明
Metropolis-Hastingsでは以下の様にアルゴリズムを定めました。
(再掲)
for i=0,1,…,do
$~~~~$# 提案分布$q(\vec z| \vec z^{(i)})$からサンプルする
$~~~~$sample $\vec z^* \sim q(\vec z| \vec z^{(i)})$
$~~~~$# 下記の通り$A(\vec z^*, \vec z^{(i)})$を定める
$~~~~$# ただし$p()$は目標分布を表す
$~~~~$$A(\vec z^*, \vec z^{(i)}) = \min\{ 1, \frac{p(\vec z^*) q(\vec z^{(i)} | \vec z^*)}{p(\vec z^{(i)} ) q(\vec z^* | \vec z^{(i)})} \}$
$~~~~$# 下記の通り$\vec z^{(i+1)}$を更新する
$~~~~$・$\vec z^{(i+1)}$←$\vec z^*$ with probability $A(\vec z^*, \vec z^{(i)})$
$~~~~$・$\vec z^{(i+1)}$←$\vec z^{(i)}$ otherwise (probability $1-A(\vec z^*,\vec z^{(i)})$)
$~~~~$end
最終的にiが一定以降(1000以降など)のサンプルを採用する。
以下証明においては、$\vec z^{(i)}, \vec z^{(i+1)}$をより一般化して、$\vec z, \vec z’$とします。
(証明)
上記アルゴリズムの下では、
$$\begin{aligned} &p(\vec z) \cdot \underbrace{\{ q(\vec z’ | \vec z) \cdot A(\vec z’, \vec z) \}}_{\vec zから\vec z’への推移確率に相当} \\ = &p(\vec z’) \cdot \underbrace{\{ q(\vec z | \vec z’) \cdot A(\vec z, \vec z’) \}}_{\vec z’から\vec zへの推移確率に相当} ~~~~~ \mathrm{(B)} \end{aligned}$$が成立します。
というのも、
$$\begin{aligned} &p(\vec z) \cdot \{ q(\vec z’ | \vec z) \cdot A(\vec z’, \vec z) \} \\[10px] = &p(\vec z) \cdot \{ q(\vec z’ | \vec z) \cdot \min\{ 1, \frac{p(\vec z’) q(\vec z | \vec z’)}{p(\vec z ) q(\vec z’ | \vec z)} \} \\ &{\scriptsize(\mathrm{(A)}より)} \\[10px] = &\min\{ p(\vec z) q(\vec z’ | \vec z), p (\vec z’) q(\vec z | \vec z’) \} \\[10px] = &p(\vec z’) \cdot \{ q(\vec z | \vec z’) \cdot \min\{ 1, \frac{p(\vec z) q(\vec z’ | \vec z)}{p(\vec z’ ) q(\vec z | \vec z’)} \} \\[10px] = &p(\vec z’) \cdot \{ q(\vec z | \vec z’) \cdot A(\vec z, \vec z’) \} \\ \end{aligned}$$となるためです。
$\mathrm{(B)}$は詳細釣り合い条件の成立に相当するため、$p()$は定常分布となる。
($p()$は目標分布を表すため、目標分布が定常分布となる)
2. Gibbs sampling
2-1. Gibbs samplingにおいて目標分布が定常分布となることの証明
Gibbs samplingでは以下の様にアルゴリズムを定めました。
(再掲)
for i=0,1,…,do
$~~~~$# Gibbs samplingではベクトルを構成する要素を1つずつ更新する
$~~~~$# $\vec z^{(i)} = (z_1^{(i)},\cdots,z_K^{(i)})$、と$K$要素からなるものとする
$~~~~$# $p()$は目標分布を表す
$~~~~$sample $z_1^{(i+1)} \sim p(z_1 | z_2^{(i)},\cdots,z_K^{(i)})$
$~~~~$sample $z_2^{(i+1)} \sim p(z_2 | z_1^{(\color{red}{i+1})},z_3^{(i)},\cdots,z_K^{(i)})$
$~~~~$・・・(以下同様)・・・
$~~~~$sample $z_K^{(i+1)} \sim p(z_K | z_1^{(\color{red}{i+1})},\cdots,z_{K-1}^{(\color{red}{i+1})})$
$~~~~$# 上記プロセスにおいては、『目標分布$p()$において、ベクトル$\vec z$を構成する要素の1つは、残りの要素が条件づけられていればsample可能(*)』という条件下で話を進めています
$~~~~$end
最終的にiが一定以降(1000以降など)のサンプルを採用する。
以下証明においては、$\vec z^{(i)}, \vec z^{(i+1)}$をより一般化して、$\vec z, \vec z’$とします。
(証明)
推移確率を表す分布を$R()$とした時、定常分布を表す定義式は、
$$\begin{aligned} p(\vec z’) = \vec \int p(\vec z) \cdot R(\vec z’ | \vec z) d \vec z \end{aligned}$$であった。
今回の文脈では具体的には、
$$\begin{aligned} p(z_1′, z_2′, z_3′) = \int \int \int p(z_1, z_2, z_3) \cdot p(z_1′ | z_2, z_3) p(z_2′ | z_1′, z_3) p(z_3′ | z_1′, z_2′) dz_1 dz_2 dz_3 ~~~~~ \mathrm{(C)} \end{aligned}$$となるので、これを以下示す。
$\mathrm{(C)}$を示す前に1つ準備をする。
$(z_1,z_2,z_3)$と$(z_1′,z_2,z_3)$との推移を考えた時、
$$\begin{aligned} &p(z_1,z_2,z_3) p(z_1′ | z_2, z_3) \\[10px] = &\underbrace{\color{red}{p(z_2, z_3)} p(z_1 | z_2, z_3)}_{p(z_1,z_2,z_3)} \color{red}{p(z_1′ | z_2, z_3)} \\[10px] = &\color{red}{p(z_1′,z_2,z_3)} p(z_1 | z_2, z_3) \end{aligned}$$となる。
示すべき$\mathrm{(C)}$の右辺に注目すると、
$$\begin{aligned} &\int \int \int \textcolor{blue}{p(z_1, z_2, z_3) p(z_1′ | z_2, z_3)} p(z_2′ | z_1′, z_3) p(z_3′ | z_1′, z_2′) dz_1 dz_2 dz_3 \\[10px] = &\int \int \int \textcolor{blue}{p(z_1′,z_2,z_3) p(z_1 | z_2,z_3)} p(z_2′ | z_1′, z_3) p(z_3′ | z_1′, z_2′) dz_1 dz_2 dz_3 \\ &{\scriptsize(上記準備を用いた)} \\[10px] = &\underbrace{\int p(z_1 | z_2,z_3) d z_1}_{=1} \cdot \int \int \textcolor{red}{p(z_1′,z_2,z_3) p(z_2′ | z_1′, z_3)} p(z_3′ | z_1′, z_2′) dz_2 dz_3 \\ = &\int \int \textcolor{red}{ p(z_1′, z_2′, z_3) p(z_2 | z_1′, z_3) } p(z_3′ | z_1′, z_2′) dz_2 dz_3 \\ &{\scriptsize(上記準備と同じ内容を用いた)} \\[10px] = &\underbrace{\int p(z_2 | z_1′, z_3) dz_2}_{=1} \cdot \int \textcolor{blue}{ p(z_1′,z_2′,z_3) p(z_3′ | z_1′, z_2′) } dz_3 \\[10px] = &\int \textcolor{blue}{ p(z_1′,z_2′,z_3′) p(z_3 | z_1′, z_2′) } dz_3 \\ &{\scriptsize(上記準備と同じ内容を用いた)} \\[10px] = &p(z_1′,z_2′,z_3′) \underbrace{\int p(z_3 | z_1′,z_2′) dz_3}_{=1} \\[10px] = &p(z_1′,z_2′,z_3′) \end{aligned}$$
以上より示すべき$\mathrm{(C)}$が示されたことになり、$p()$は定常分布となる。
($p()$は目標分布を表すため、目標分布が定常分布となる)

