$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}} \\ \gdef \tr {\mathrm{tr}}$
分割表は$\chi^2$検定やら適合度検定やらたくさんの検定方式がでてきて大変なイメージがあります。
まずは『分割表の統計モデル』を整理するところから始めましょう。
これまで分割表に統計モデルを当てはめるという話を聞いたことはなく、検定方式を盲目的に暗記してました。
『分割表の統計モデル』を整理しておくと盲目的な暗記は不要となります。
分割表は以下の3つのパターンにわけて考えることができます:
①どこもfixされない場合
②総和がfixされる場合
③列和または行和がfixされる場合
今回は各パターンに対して想定される統計モデルを紹介します。
各パターンにおいて、まずはフルモデルを紹介し、その後にある制約条件(帰無仮説に相当)をつけたモデルを紹介するという流れをとります。
その様な整理は初めて聞きましたが、ゆっくりと整理していきたいと思います。
次回以降の記事では上記3パターンに基づく推定・検定を行うので、ここでこの3パターンについてしっかりと押さえておいてください。
0. 導入
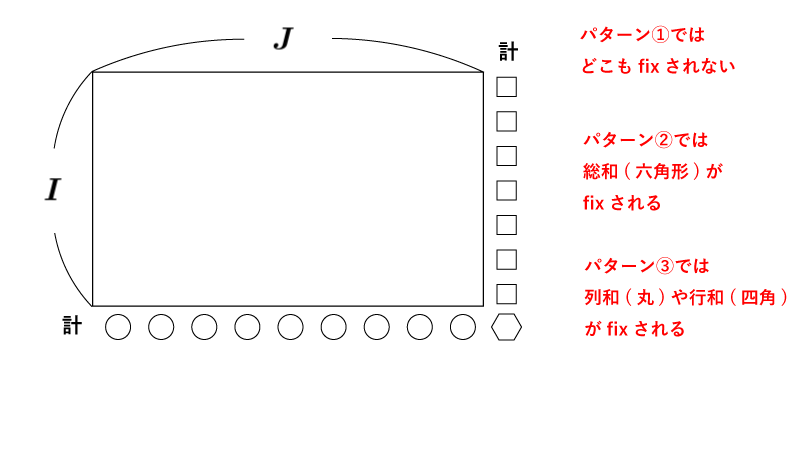
以下$I$行$J$列の分割表を以下の様な3つのパターンに分けて考えます。
なお、$(i,j)$セルの度数を$X_{ij}$とします。
①どこもfixされない場合
②総和がfixされる場合
③列和または行和がfixされる場合
図で示すと以下の様になります。
1. どこもfixされない場合
各セルの度数はポアソン分布に従うというモデルを想定することができます。
(ポアソン分布に限定されるわけではなく、カウントデータをモデリングできるものであれば構いません。例:負の二項分布)
つまり、同時確率関数$p(x)$は、
$$\begin{aligned} p(x) &= \prod_{i,j} e^{-\theta_{ij}} \frac{\theta_{ij}^{x_{ij}}}{x_{ij}!} ~~~~~ \mathrm{(A)} \\ &{\scriptsize(X_ij \sim \Po(\theta_{ij})とした)} \end{aligned}$$となり、パラメータの自由度は$IJ$となります。
どこもfixされないため$\theta_{ij}$についての条件がつかず、$\theta_{ij}$は自由に決まるため、パラメータの自由度が$IJ$となるのですね。
$\mathrm{(A)}$のみ条件が課されたモデルがフルモデルです。
ここで、パラメータ$\theta_{ij}$について、
$$\begin{aligned} \log \theta_{ij} &= \mu + \alpha_i + \beta_j + \gamma_{ij} ~~~~~ \mathrm{(B)} \\ &{\scriptsize(ただし、\textcolor{red}{\sum_i \alpha_i = \sum_j \beta_j = \sum_i \gamma_{ij} = \sum_j \gamma_{ij} = 0})} \end{aligned}$$としたパラメータの変換(パラメトライズ)を行い、 ある制約条件(帰無仮説に対応)$H_0$が課されたモデルを考えてみます。
●${\small 帰無仮説} H_0: \gamma_{ij} = 0 ~~ {\small (\forall i, j)} ~~~~~ \mathrm{(C)}$
この時、$\log \theta_{ij} = \mu + \alpha_i + \beta_j$、となりますが、$\mu, \alpha_i, \beta_j$の自由度はそれぞれ$1,I-1,J-1$となるので、パラメータの自由度は$(I+J+1)$となります。
前者のモデル(フルモデル)は$\mathrm{(A)}$が、後者のモデルは$\mathrm{(A),(B),\color{red}{(C)}}$が課されたモデルになってるのですね。
その通りです。なお、$\mathrm{(B)}$で行った$\theta_{ij} \leftrightarrow \mu, \alpha_i, \beta_j, \gamma_{ij}$の変換ですが、これを行ったことで$\mathrm{(C)}$の様に帰無仮説をシンプルに置くことができました。$\mathrm{(B)}$の変換を行わずに$\mathrm{(C)}$と同じ意味の帰無仮説を置くこともできるはずですが、より複雑になります。なお、$\mathrm{(B)}$の変換はモデルに用いるパラメータの見せ方を変えただけであり、これによってモデルが表すものは変わりません。
例1.
同じ大きさの町(A町、B町、C町)ごとに、年間の交通事故の情報が以下の様に得られた。
| 2018 | 2019 | 2020 | 2021 | |
| A町 | 105 | 98 | 102 | 91 |
| B町 | 101 | 99 | 102 | 105 |
| C町 | 110 | 108 | 105 | 102 |
この例ではどこもfixされておらず、各セルの度数は独立に(異なるパラメータの)ポアソン分布に従うというモデルを想定することができます。
帰無仮説として$\mathrm{(C)}$の様においた時、これは『町と年の交互作用がない』(『「町」による効果が「年」により変わらない、または、『「年」による効果が「町」により変わらない』)と同義になります。
2. 総和がfixされる場合
各セルの度数は$IJ$項分布に従うというモデルを想定することができます。
つまり、同時確率関数$p(x)$は、
$$\begin{aligned} p(x) &= \frac{n!}{\prod_{i,j} x_{ij}!} \prod_{i,j} p_{ij}^{x_{ij}} ~~~~~ \mathrm{(D)} \\ &{\scriptsize(X_ij \sim \Bin(n,p_{ij})とした)} \end{aligned}$$となり、パラメータの自由度は$(IJ-1)$となります。
($\sum_{i,j} p_{ij}=1$、という$1$つの制約条件があるので自由度は『1. どこもfixされない場合』よりも$1$下がります)
$\mathrm{(D)}$のみ条件が課されたモデルがフルモデルです。
ここである制約条件(帰無仮説に対応)として以下$H_0$が課されたモデルを考えてみます。
●${\small 帰無仮説} H_0: p_{ij} = p_{i \bullet} p_{\bullet j} ~~ {\small (\forall i, j)} ~~~~~ \mathrm{(E)}$
この時、パラメータの自由度は$(I-1) + (J-1)$となります。
$\mathrm{(D),(E)}$の下では、$p_{ij}$は$p_{i \bullet}, p_{\bullet j}$から自動できまるので、結局自由に決められるのは$p_{i \bullet}$についての$(I-1)$通り、$p_{\bullet j}$についての$(J-1)$通りというところから由来するのですね。
その通りです。
なお、この帰無仮説$H_0$の検定のことを巷では『独立性の検定』と言います。
例2.
ある市町村でランダム抽出した合計150名の血液型の情報が以下の様に得られた。
なお元号「昭和」「平成」「令和」はその人が生まれた元号を表す。
| A | B | O | AB | |
| 昭和 | 20 | 10 | 16 | 6 |
| 平成 | 15 | 12 | 16 | 4 |
| 令和 | 17 | 13 | 14 | 7 |
この例では総和がfixされており(150)、各セルの度数は12項分布に従うというモデルを想定することができます。
帰無仮説として上記$\mathrm{(E)}$の様においた時、これは『生まれた元号と血液型の交互作用がない』(元号が何であろうと血液型の分布は変わらない、または、血液型が何であろうと元号の分布は変わらない)と同義になります。
あくまでも総和が150とfixされているわけで、「昭和」「平成」「令和」それぞれの行和が50ではないことに気をつけてください。
3. 列和または行和がfixされる場合
(ここでは列和がfixされる場合を扱いますが、行和がfixされる場合も同様です)
列和がfixされる場合、各セルの度数は$I$項分布$(\times J)$に従うというモデルを想定することができます。
つまり、同時確率関数$p(x)$は、
$$\begin{aligned} p(x) &= \prod_{j} \{ \frac{n_j!}{\prod_i x_{ij}!} \prod_i p_{ij}^{x_{ij}} \} ~~~~~ \mathrm{(F)} \end{aligned}$$となり、パラメータの自由度は$(I-1) \times J$となります。
($I$項分布のパラメータの自由度は$(I-1)$であることから由来)
$\mathrm{(F)}$のみ条件が課されたモデルがフルモデルです。
ここである制約条件(帰無仮説に対応)として以下$H_0$が課されたモデルを考えてみます。
●${\small 帰無仮説} H_0: p_{i1} = p_{i2} = \cdots = p_{iJ} ~~ (\forall i) ~~~~~ \mathrm{(G)}$
この時、パラメータの自由度は$(I-1)$となります。
パラメータの自由度はそのまんまですね。なお、この帰無仮説$H_0$の検定のことをちまたでは『一様性の検定』と言います。
例3.
ある市町村で生まれた元号ごとに50名ずつランダム抽出した合計150名の血液型の情報が以下の様に得られた。
| A | B | O | AB | |
| 昭和 | 21 | 10 | 14 | 5 |
| 平成 | 16 | 12 | 16 | 6 |
| 令和 | 17 | 13 | 14 | 6 |
この例では各行和はfixされており(50)、各セルの度数は4項分布$(\times 3)$に従うというモデルを想定することができます。
帰無仮説として$\mathrm{(G)}$の様においた時、これは『生まれた元号によらず血液型の内訳は一様』と同義になります。
結果的に総和も150とfixされることになりますが、それより強い制約条件として各行和が50であることに気をつけてください。
まとめ.
- 分割表の統計モデルは、どこがfixされるのかにより3パターンに分類して考えるのがよい。






