$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}}$
教科書にのっているサンプルサイズ設計の公式を使えば一応の計算はできますが、その内容については正直わかりきっていません。。
そうですか。
そもそもですが、なぜサンプルサイズ設計をするのでしょうか?
えっ。。そう問われるとさっと答えることができません。
その解答は肝なので、まずしっかりと確認しましょう。
0. サンプルサイズ設計をする理由
ある母集団についてその分布パラメータの検定・区間推定をしたい時、母集団全体を解析対象とすることは通常困難であるため、母集団から一定人数をランダム抽出して解析対象とします。
ランダム抽出する人数の設計(計算)を「サンプルサイズ設計」と言います。
サンプルサイズ設計をする理由を考えるにあたり、一例として、
$$\begin{aligned} \begin{cases} {\small 帰無仮説}H_0: \mu \leqq 0 \\ {\small 対立仮説}H_1: \mu \gt 0 \end{cases} \end{aligned}$$という有意水準$\alpha$の片側検定を考えます。
この時、検出力関数*(『真のパラメータ値』を$x$軸に、『検出力**』を$y$軸においた関数)のグラフは以下Fig1の様になります。
(ただし、『実用上意味のある最小の差』を$20$と設定しています)
Fig1. (濃い青の曲線はより大きなサンプルサイズnに対応します)
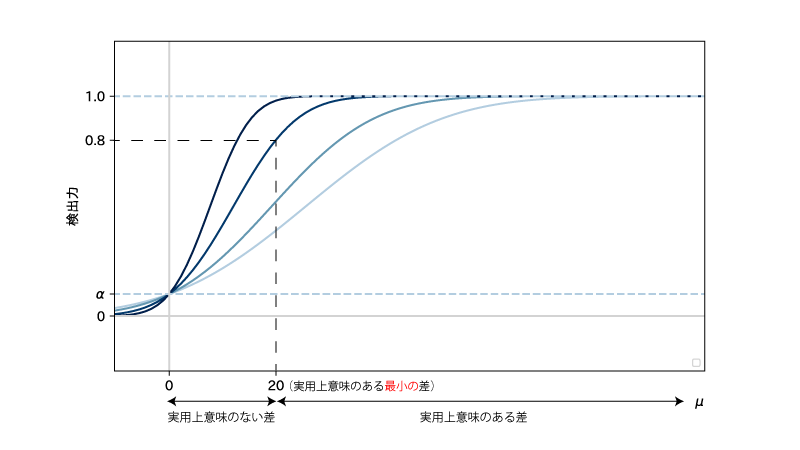
(グラフより)『真の差』がどんなに小さな正の値だったとしても、その値における検出力は nを大きくとるほど高くなります。
しかし、実用上意味のない小さな差は重要ではなく(例. 血圧1mmHgの違い)、その値における検出力は高くある必要はありません。
よって『実用上意味のある最小の差』を定めて、その点における検出力がある値(例. 0.8 )になる様に$n$を設計する、という姿勢が求められます。
Fig1においては、実用上意味のある最小の差として$20$を定め、そこでの検出力が$0.8$になっている(2番目に濃い青の)曲線に対応する$n$がよいということですね。1番目に濃い青の曲線では実用上意味のない差まで検出力$0.8$で検出してしまうため、無駄に$n$が大きくなっているのですね。
そうですね。臨床研究にはコストがかかりますし、ものによっては対象患者さんに被害が生じうるものもあるので、$n$を適切な範囲に抑えることは、コストや被害を最小にすることにつながります。
(補足)
- *:検出力関数の一例: $X_i \overset{i.i.d}\sim \N(\mu, 1^2) ~~ {\small (i=1, \ldots, n)}$である時、
$$\begin{aligned} \begin{cases} {\small (帰無仮説)}H_0: \mu \leqq 0 \\ {\small (対立仮説)}H_1: \mu \gt 0 \end{cases} \end{aligned}$$という有意水準$\alpha$の片側検定を考えます。
検定統計量$Z$を、
$$\begin{aligned} Z = \frac{\bar{X}_n-0}{\frac{1}{\sqrt{n}}} = (\sqrt{n} \bar{X}_n) \end{aligned}$$とおくと、検出力関数の値$Pr_{\mu}\{ Z \gt z_{\alpha} \}$は、
(ただし$z_{\alpha}$を標準正規分布の上側$\alpha$点とする)
$$\begin{aligned} Pr_{\mu}\{ Z \gt z_{\alpha} \} &= Pr_{\mu}\{ \sqrt{n} \bar{X}_n \gt z_{\alpha} \} \\[10px] &= Pr_{\mu}\{ \underbrace{\sqrt{n} (\bar{X}_n-\mu)}_{\sim \N(0, 1)} \gt z_{\alpha}-\sqrt{n} \mu \} \\[10px] &= 1-\Phi(z_{\alpha}-\sqrt{n}\mu) ~~~~~ \mathrm{(A)} \\ &{\scriptsize (ただし\Phi(\bullet)は\N(0,1)の分布関数)} \end{aligned}$$となります。
$\mathrm{(A)}$より検出力$Pr_{\mu}\{ Z \gt z_{\alpha} \}$は$\mu$についての単調増加関数であることがわかり、$\mu: -\infty \sim \infty$の範囲で$Pr_{\mu }\{ Z \gt z_{\alpha} \}: 0 \sim 1$の範囲を動くので、検出力関数はFig1の様になります。また$\mathrm{(A)}$より、あるfixされた$\mu$について$n$が大きくなるほど検出力関数の値$Pr_{\mu}\{ Z \gt z_{\alpha} \}$が大きくなることもわかります。 - **:検出力関数のy軸は厳密には『検出力』ではなく、『対立仮説を採択する確率(帰無仮説を棄却する確率)』とするべきです。というのも$\mu \gt 0$では対立仮説が正しいという想定がされ『対立仮説を採択する確率(帰無仮説を棄却する確率)』を『検出力』と呼びますが、$\mu \leqq 0$では帰無仮説が正しいという想定がされ『対立仮説を採択する確率(帰無仮説を棄却する確率)』を『検出力』と呼ばないからです。ただ、ここでは『検出力関数』という言葉のイメージを重視して、あえて『検出力』という言葉を用いました。
1. サンプルサイズ設計の具体的な流れ
$X_i \overset{i.i.d}\sim \N(\mu, \sigma^2) ~~ {\small (i=1, \ldots, n)}$である時、
$$\begin{aligned} \begin{cases} {\small (帰無仮説)}H_0: \mu \leqq \mu_0 \\ {\small (対立仮説)}H_1: \mu \gt \mu_0 \end{cases} \end{aligned}$$という有意水準$\alpha$の片側検定を考えます。
(ただし$\sigma^2$は既知とします)
ただし、『実用上意味のある最小の差』を$\mu_1$として、それを検出力$(1-\beta)$で検出したいものとします。
この時、検定統計量$Z$を、
$$\begin{aligned} Z = \frac{\bar{X}_n-\mu_0}{\frac{\sigma}{\sqrt{n}}} \end{aligned}$$とおくと、検出力関数の値$Pr_{\mu}\{ Z \gt z_{\alpha} \}$は、
$$\begin{aligned} Pr_{\mu}\{ Z \gt z_{\alpha} \} &= Pr_{\mu}\{ \frac{\bar{X}_n-\mu_0}{\frac{\sigma}{\sqrt{n}}} \gt z_{\alpha} \} \\[10px] &= Pr_{\mu}\{ \frac{\bar{X}_n-\mu}{\frac{\sigma}{\sqrt{n}}} \gt z_{\alpha}-\frac{\mu-\mu_0}{\frac{\sigma}{\sqrt{n}}} \} \\ &{\scriptsize (\frac{\bar{X}_n-\mu}{\frac{\sigma}{\sqrt{n}}} (\sim \N(0,1))を無理やり作り出した)} \\[10px] &= 1-\Phi(z_{\alpha}-\frac{\mu-\mu_0}{\frac{\sigma}{\sqrt{n}}}) \\ &{\scriptsize (ただし\Phi(\bullet)は\N(0,1)の分布関数)} \end{aligned}$$となります。
よって、$\mu=\mu_1$の時の検出力を$(1-\beta)$としたいので、
$$\begin{alignat}{2} \notag && \left. Pr_{\mu}\{ Z \gt z_{\alpha} \} \right|_{\mu=\mu_1} &= 1-\beta \\[10px] \notag &\Rightarrow& \left. \{ 1-\Phi(z_{\alpha}-\frac{\mu-\mu_0}{\frac{\sigma}{\sqrt{n}}}) \} \right|_{\mu=\mu_1} &= 1-\beta \\[10px] \notag &\Rightarrow& \Phi(z_{\alpha}-\frac{\mu_1-\mu_0}{\frac{\sigma}{\sqrt{n}}}) &= \beta \\[10px] \notag &\Rightarrow& z_{\alpha}-\frac{\mu_1-\mu_0}{\frac{\sigma}{\sqrt{n}}} (&= z_{1-\beta}) = -z_{\beta} \\[10px] \notag &\Rightarrow& z_{\alpha} + z_{\beta} &= \frac{\mu_1-\mu_0}{\frac{\sigma}{\sqrt{n}}} \\[10px] \notag &\Rightarrow& n &= \left\{ \frac{z_{\alpha} + z_{\beta}}{(\frac{\mu_1-\mu_0}{\sigma})} \right\}^2 ~~~~~ \mathrm{(B)} \end{alignat}$$となります。
補足.
- $\mathrm{(B)}$の各要素の決め方は研究分野によりますが、臨床研究ではおおよそ以下の通りです。
・$Z_{\alpha}$:$Z_{0.05}$または$Z_{0.025}$
・$Z_{\beta}$:$Z_{0.2}$や$Z_{0.1}$など
・$\mu_1$:『実用上意味のある最小の差』として定める。ただし、『実用上意味のある差』が定まっていない場合には『見込まれる差』を研究者が定める。
・$\mu_0$:薬の効果の差を比較する場合などは$0$がよく用いられる。
・$\sigma$:先行研究のデータから基本的に見積もる。(または見積もりが困難な場合にはサンプルサイズ設計自体を$\t$検定に基づいて行うことも可能)
- ここまで両側検定ではなくなぜ片側検定を扱ってきたのかを疑問に思う方がいるかと思います。両側検定の場合には$\mathrm{(B)}$に対応するものとして、
$$\begin{aligned} n &= \left\{ \frac{Z_{\color{red}{\frac{\alpha}{2}}} + Z_{\beta}}{(\frac{\mu_1-\mu_0}{\sigma})} \right\}^2 ~~~~~ \mathrm{(B’)} \end{aligned}$$となりますが、実はこの導出には近似が含まれています。
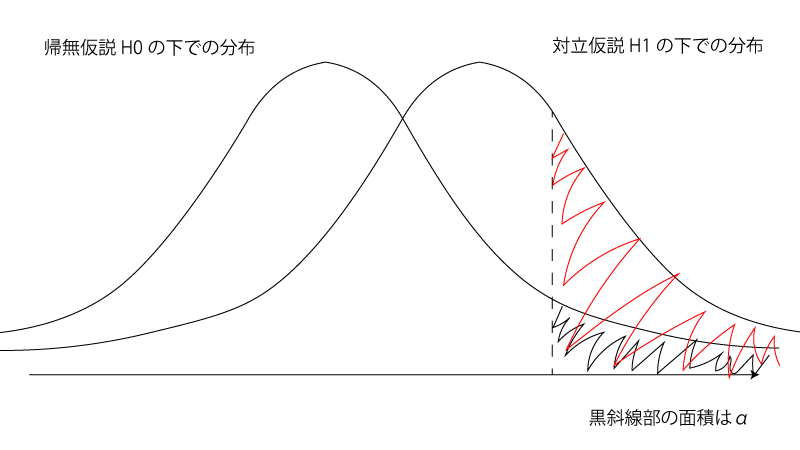
というのも有意水準$\alpha$の片側検定の場合にはFig2の赤斜線部が検出力に相当しますが、
Fig2.
有意水準$\alpha$の両側検定の場合にはFig3の赤斜線部+うす青斜線部が検出力に相当します。
Fig3.
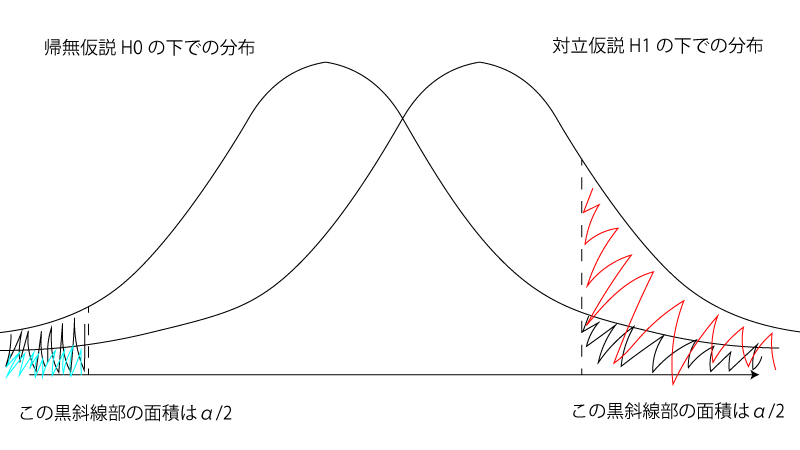
通常は赤斜線部に対してうす青斜線部は無視され(近似)、その様にすれば両側検定でも片側検定の場合と同様に$\mathrm{(B’)}$が導出されます。 本記事では近似をせずに話を進められる様に片側検定を扱った次第です。
まとめ.
- サンプルサイズ設計とは、ある有意水準$\alpha$の下で『実用上意味のある最小の差』をある検出力$(1-\beta)$で検出するためのサンプルサイズを設計する行為である。
- 適切なサンプルサイズ設計により、お金・時間・労力を適切な範囲内に抑えた上で妥当な検定を行うことができる。






