$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}} \\ \gdef \indep {\mathop{\perp\!\!\!\!\perp}} \\ \gdef \tr {\mathrm{tr}}$
(証明すべき内容の再掲)
サンプリングの過程が『0. 前提』(@<フィッシャーの正確検定>)のいずれの場合でも、
$$\begin{aligned} Pr\{ (X_{11}, X_{12}, X_{21}, X_{22}) &= (x_{11}, x_{12}, x_{21}, x_{22}) | x_{1 \bullet}, x_{2 \bullet}, x_{\bullet 1}, x_{\bullet 2} \} \\[10px] &= \frac{ \displaystyle \binom{ x_{\bullet 1} }{ x_{11} } \displaystyle \binom{ x_{\bullet 2} }{ x_{12} } }{ \displaystyle \binom{ x_{\bullet \bullet} }{ x_{1 \bullet} } } (= \frac{ \displaystyle \binom{ x_{1 \bullet} }{ x_{11} } \displaystyle \binom{ x_{2 \bullet} }{ x_{21} } }{ \displaystyle \binom{ x_{\bullet \bullet} }{ x_{\bullet 1} } } ) \\[10px] &= \frac{x_{\bullet 1}! x_{2 \bullet}! x_{\bullet 1}! x_{\bullet 2}! }{ x_{\bullet \bullet}! } \cdot \frac{1}{ x_{11}! x_{12}! x_{21}! x_{22}! } \end{aligned}$$
(ただし、$\max\{ 0, x_{\bullet 1}-(x_{\bullet \bullet}-x_{1 \bullet}) \} \leqq x_{11} \leqq \min\{x_{1 \bullet}, x_{\bullet 1} \}$)
と、超幾何分布の確率関数の形になる。
サンプリングの過程として以下の3通りがあると紹介しました。
・①どこもfixされない場合
・②総和がfixされる場合
・③列和または行和がfixされる場合
サンプリングが①②の場合については、下記の通り、列和または行和がfixされるという条件付けをしたもとでは、サンプリングが③の場合と同じになります。(下記参照)
サンプリングが①の場合:各セルの度数はポアソンモデルなどに従うと想定できる
↓
↓総和をfixすると
↓
各セルの度数は多項分布に従うと想定できる
(これはサンプリングが②の場合に相当)
↓
↓列和または行和をfixすると
↓
各セルの度数は2項分布(×2)に従うと想定できる
(これはサンプリングが③の場合に相当)
サンプリングが②の場合:各セルの度数は多項分布に従うと想定できる
↓
↓列和または行和をfixすると
↓
各セルの度数は2項分布(×2)に従うと想定できる
(これはサンプリングが③の場合に相当)
フィッシャーの正確検定においては、サンプリングの過程がいずれの場合でも、列和と行和をfixした条件づけの下での条件つき確率を考えることになります。
つまりは、サンプリングの過程が③である場合に上記証明ができれば、サンプリングの過程が①②である場合の証明は不要であることがわかります。
よって以下は、サンプリングの過程が③である場合の証明をします。
(証明)
ここではサンプリングの過程として列和がfixされる場合、つまり、
$$\begin{aligned} X_{11} + X_{21} &= x_{\bullet 1} \\ X_{21} + X_{22} &= x_{\bullet 2} \end{aligned}$$とfixされる場合を考える。
この場合、各セルの度数$X_{ij} ~~ \small{(i=1,2;j=1,2)}$は$2$項分布$(\times 2)$に従うというモデルを想定することができ、明示すると、
$$\begin{aligned} X_{11} &\sim \Bin(x_{\bullet 1},p_{11}) \\ X_{12} &\sim \Bin(x_{\bullet 2},p_{12}) \\ (X_{21}&=x_{\bullet 1}-X_{11}) \\ (X_{22}&=x_{\bullet 2}-X_{12}) \end{aligned}$$となる。
フィッシャーの正確検定においては、列和と行和をfixした条件づけの下での条件つき確率を考えることになるので、今回の場合には、行和を追加でfixした状況を考えることになる。(以下Fig参照)
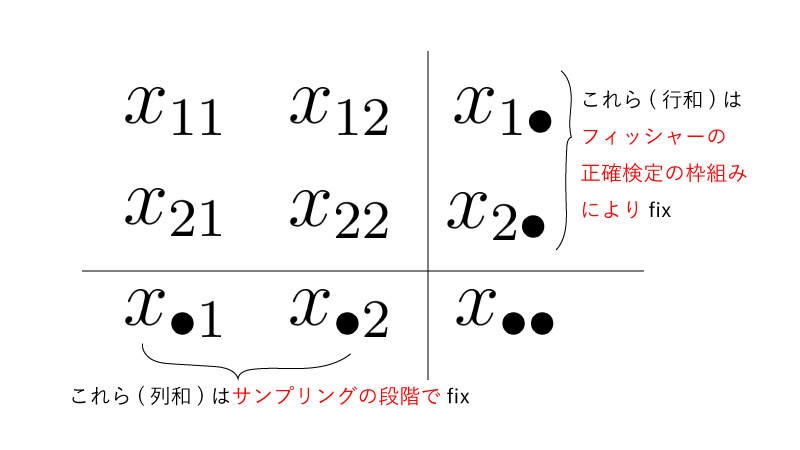
$Pr\{ (X_{11}, X_{12}, X_{21}, X_{22}) = (x_{11}, x_{12}, x_{21},x_{22}) | x_{1 \bullet}, x_{2 \bullet}, x_{\bullet 1},x_{\bullet 2} \}$について、今回はサンプリングの段階で$x_{\bullet 1}, x_{\bullet 2}$はfixされているため、条件づけに$x_{\bullet 1}, x_{\bullet 2}$を含める必要はなく、$Pr\{ (X_{11}, X_{12}, X_{21}, X_{22}) = (x_{11}, x_{12}, x_{21},x_{22}) | x_{1 \bullet}, x_{2 \bullet} \}$と同じである。
これについて考えると、
$$\begin{aligned} &Pr\{ (X_{11}, X_{12}, X_{21}, X_{22}) = (x_{11}, x_{12}, x_{21},x_{22}) | x_{1 \bullet}, x_{2 \bullet} \} \\[10px] = &Pr\{ X_{11} = x_{11} | x_{1 \bullet}, x_{2 \bullet} \} \\ &{\scriptsize (行和と列和がfixされてるためX_{11}のみ定まれば残りのセルは定まる)} \\[10px] = &Pr\{ X_{11} = x_{11} | x_{1 \bullet} \} \\ &{\scriptsize (総和はx_{1 \bullet} + x_{2 \bullet}であるため、x_{1 \bullet}を条件づければx_{2 \bullet} = x_{1 \bullet} + x_{2 \bullet}-x_{1 \bullet}と定まる)} \\[10px] =& \dfrac{Pr \{ X_{11} = x_{11}, X_{11} + X_{12} = x_{1 \bullet} \}} { Pr \{X_{11} + X_{12} = x_{1 \bullet} \} } \\[10px] =& \dfrac{Pr \{ X_{11} = x_{11}, X_{12} = x_{1 \bullet}-x_{11} \}} { Pr \{X_{11} + X_{12} = x_{1 \bullet} \} } \\[10px] =& \dfrac { \displaystyle \binom{ x_{\bullet 1} }{ x_{11} } p_{11}^{x_{11}} (1-p_{11})^{x_{\bullet 1}-x_{11}} \cdot \displaystyle \binom{ x_{\bullet 2} }{ x_{1 \bullet}-x_{11} } p_{21}^{x_{1 \bullet}-x_{11}} (1-p_{21})^{x_{\bullet 2}-(x_{1 \bullet}-x_{11})} } { \displaystyle \sum_{ \max \{ 0, x_{1 \bullet}-x_{\bullet 2} \} \leqq x’_{11} \leqq \min \{ x_{1 \bullet},x_{\bullet 1} \} } \displaystyle \binom{ x_{\bullet 1} }{ x’_{11} } p_{11}^{x’_{11}} (1-p_{11})^{x_{\bullet 1}-x’_{11}} \cdot \displaystyle \binom{ x_{\bullet 2} }{ x_{1 \bullet}-x’_{11} } p_{21}^{x_{1 \bullet}-x’_{11}} (1-p_{21})^{x_{\bullet 2}-(x_{1 \bullet}-x’_{11})} } \\ &{\scriptsize (分母の\sum内部は分子のx_{11}をx’_{11}に置換しただけ。前式からの分母の変形については下記参照*)} \\[10px] =& \dfrac { \displaystyle \binom{ x_{\bullet 1} }{ x_{11} } \left( \frac{p_{11}}{1-p_{11}} \right)^{x_{11}} \textcolor{red}{(1-p_{11})^{x_{\bullet 1}}} \cdot \displaystyle \binom{ x_{\bullet 2} }{ x_{1 \bullet}-x_{11} } \left( \frac{1-p_{21}}{p_{21}} \right)^{x_{11}} \textcolor{red}{p_{21}^{x_{1 \bullet}} (1-p_{21})^{x_{\bullet 2}-x_{1 \bullet}}} } { \displaystyle \sum_{ \max \{ 0, x_{1 \bullet}-x_{\bullet 2} \} \leqq x’_{11} \leqq \min \{ x_{1 \bullet},x_{\bullet 1} \} } {\small (分子のx_{11}をx’_{11}に置換したもの)} } \\[10px] =& \dfrac { \displaystyle \binom{ x_{\bullet 1} }{ x_{11} } \displaystyle \binom{ x_{\bullet 2} }{ x_{1 \bullet}-x_{11} } \left( \frac{p_{11} p_{22}}{p_{12} p_{21}} \right)^{x_{11}} } { \displaystyle \sum_{ \max \{ 0, x_{1 \bullet}-x_{\bullet 2} \} \leqq x’_{11} \leqq \min \{ x_{1 \bullet},x_{\bullet 1} \} } {\small (分子のx_{11}をx’_{11}に置換したもの)} } \\ &{\scriptsize (前式の赤文字部分は分母分子で打ち消し合う)} \\[10px] =& \dfrac { \displaystyle \binom{ x_{\bullet 1} }{ x_{11} } \displaystyle \binom{ x_{\bullet 2} }{ x_{1 \bullet}-x_{11} } } { \displaystyle \sum_{ \max \{ 0, x_{1 \bullet}-x_{\bullet 2} \} \leqq x’_{11} \leqq \min \{ x_{1 \bullet},x_{\bullet 1} \} } {\small (分子のx_{11}をx’_{11}に置換したもの)} } ~~~~~ \mathrm{(A)} \\ &{\scriptsize (帰無仮説の下で\frac{p_{11} p_{22}}{p_{12} p_{21}}=1)} \\[10px] =& \dfrac{ \displaystyle \binom{ x_{\bullet 1} }{ x_{11} } \displaystyle \binom{ x_{\bullet 2} }{ x_{12} } }{ \displaystyle \binom{ x_{\bullet \bullet} }{ x_{1 \bullet} } } ~~~~~ \mathrm{(B)} \\ &{\scriptsize (分母の変形は下記参照**)} \end{aligned}$$
よって、題意は示された。
(補足*)
$\sum$における$x’_{11}$の範囲がどのように決定されるのかを説明します。
まず元々の$X_{11}$の定義域は、
$$\begin{aligned} 0 \leqq X_{11} \leqq X_{\bullet 1} \end{aligned}$$です。
また、
$$\begin{alignat}{2} &&X_{11} + X_{12} &= X_{1 \bullet} \notag \\[10px] &\Rightarrow& X_{11} &= X_{1 \bullet}-X_{12} \notag \\[10px] &\Rightarrow& X_{1 \bullet}-\max X_{12} \leqq &X_{11} \leqq X_{1 \bullet}-\min X_{12} \notag \\[10px] &\Rightarrow& X_{1 \bullet}-X_{\bullet 2} \leqq &X_{11} \leqq X_{1 \bullet} \notag \end{alignat}$$という制約がつく。
よって、
$$\begin{aligned} \max \{ 0, x_{1 \bullet}-x_{\bullet 2} \} \leqq x’_{11} \leqq \min \{ x_{1 \bullet},x_{\bullet 1} \} \end{aligned}$$
(補足**)
$\mathrm{(A)}$の分母から$\mathrm{(B)}$の分母への変形を説明します。
$\mathrm{(B)}$の分母は、$x_{\bullet \bullet}$個から$x_{1 \bullet}$個を選択する組み合わせの個数です。
一方で$\mathrm{(A)}$の分母は、$x_{\bullet \bullet}$個から$x_{1 \bullet}$個を選択するにあたって、
step1:形式上$x_{\bullet 1}$個、$x_{\bullet 2}(=x_{\bullet \bullet}-x_{\bullet 1})$個に分割する
step2:$x_{\bullet 1}$個側から$x’_{11}$個を、$x_{\bullet 2}(=x_{\bullet \bullet}-x_{\bullet 1})$個側から$(x_{1 \bullet}-x’_{11})$個を選択する
というプロセスを踏んでいると見なすことができます。
つまるところ、両者は一致します。
