『分散のくり返しの公式』は『期待値のくり返しの公式』よりやや複雑に見えますが、例を通じて理解していきましょう!
1. 『分散のくり返しの公式』
1-1. 『分散のくり返しの公式』の説明
($X, Y$は確率変数とします)
分散のくり返しの公式として、
$$ \begin{aligned} \boldsymbol{V^X[X] = E^Y[V^{X|Y}[X|Y]] + V^Y[E^{X|Y}[X|Y]]} ~~~~~ \mathrm{(A)} \end{aligned}$$ が成立します。
- 期待値のくり返しの公式:$E^X[X] = E^Y[ E^{X|Y}[X|Y] ]$、は右辺が1項でしたが、分散のくり返しの公式では$\mathrm{(A)}$の通り2項となっています。
- 直観的には$V^X[X] = E^Y[V^{X|Y}[X|Y]]$ではないかと思ってしまいますが、そうではない点に注意してください!
つまり、全体の分散($V^X[X]$)は各層での分散の平均($E^Y[V^{X|Y}[X|Y]]$)だけでは説明ができず(過小評価してしまう)、さらに層間での平均の散らばり($V^Y[E^{X|Y}[X|Y]]$)も必要になります。
分散のくり返しの公式も期待値のくり返しの公式と同じくイメージがやや難しいですが、以下の例を通じてイメージを確立してください。
例1.
ある製品は国内の$2$ヶ所の工場A, Bでのみ生産されており、それぞれの製品寿命の平均は$\displaystyle \frac{5}{2}$年、$4$年、分散は$\displaystyle \frac{1}{4}$、$\displaystyle \frac{8}{3}$であると報告されている。また、工場A, Bで生産された商品の流通割合は$4:6$であることがわかっている。
この時、手元に届いた製品の製品寿命の分散を考える。
確率変数$X, Y$をそれぞれ製品寿命、製品が生産された工場($y=0, 1$が工場A, Bに対応)とすると、$$ \begin{aligned} V^{X|Y}[X|Y=y] &= \begin{cases} \displaystyle \frac{1}{4} ~~ (y=0) \\[10px] \displaystyle \frac{8}{3} ~~ (y=1) \end{cases} \\[10px] E^{X|Y}[X|Y=y] &= \begin{cases} \displaystyle \frac{5}{2} ~~ (y=0) \\[10px] ~4 ~~ (y=1) \end{cases} \\ Pr\{ Y=0 \} &= \frac{4}{10} \\ Pr\{ Y=1 \} &= \frac{6}{10} \end{aligned}$$ となる。
この時、$V^X[X]$は $$\begin{aligned} V^X[X] &= E^Y[V^{X|Y}[X|Y]] + V^Y[E^{X|Y}[X|Y]] \\ &{\scriptsize (分散のくり返しの公式より)} \\[10px] &= \sum_y \{ V^{X|Y}[X|Y=y] \cdot Pr\{ Y=y \} \} \\ &+ \sum_y \left[\{ E^{X|Y}[X|Y=y] – E^Y[E^{X|Y}[X|Y=y]] \}^2 \cdot Pr\{ Y=y \} \right] \\[20px] &= \left\{ \frac{1}{4} \cdot Pr\{ Y=0 \} + \frac{8}{3} \cdot Pr\{ Y=1 \} \right\} \\ &+ \sum_y \left[\{ E^{X|Y}[X|Y=y] – E^X[X] \}^2 \cdot Pr\{ Y=y \} \right] \\ &{\scriptsize (期待値のくり返しの公式より E^Y[ E^{X|Y}[X|Y]] = E^X[X])} \\[10px] &= \left\{ \frac{1}{4} \cdot \frac{4}{10} + \frac{8}{3} \cdot \frac{6}{10} \right\} \\ &+ \left\{ (\frac{5}{2} – 3.4)^2 \cdot Pr\{ Y=0 \} + (4 – 3.4)^2 \cdot Pr\{ Y=1 \} \right\} \\ &{\scriptsize (E^X[X]=3.4は<期待値のくり返しの公式>:例1より)} \\[10px] &= 2.24 \end{aligned}$$
この例の様に$V^{X|Y}[X|Y], E^{X|Y}[X|Y]$と$Y$の確率関数(確率密度関数)しか与えられない場合には、この様な場合には分散のくり返しの公式が役立ちます。
イメージをより確立するためにもう1つ例を確認してみましょう!
例2.
高血圧の患者さんを対象として、薬A vs 薬B、という臨床試験を行ったとする。
この時、確率変数$X, Y$を以下の通りとする。
$$ \begin{aligned} &X: {\small (薬の内服後の)血圧} \\ &Y: \begin{cases} 1 ~~ {\small (薬\mathrm{A})} \\ 0 ~~ {\small (薬\mathrm{B})} \end{cases} \end{aligned}$$
すると、$V^X[X]$は『薬Aを内服した患者さんと薬Bを内服した患者さんを合算した全患者さん、における血圧の分散』となる。
一方で、 $E^Y[V^{X|Y}[X|Y]]$は『薬Aを内服した患者さんにおける血圧の分散と、薬Bを内服した患者さんにおける分散の、重みづけ平均』に、 $V^Y[E^{X|Y}[X|Y]]$は『薬Aを内服した患者さんにおける血圧の平均と、薬Bを内服した患者さんにおける平均の、分散』になる。
1-2. 『分散のくり返しの公式』のイメージFig
『分散のくり返しの公式』のイメージFigは以下Fig1の様になります。
Fig1.
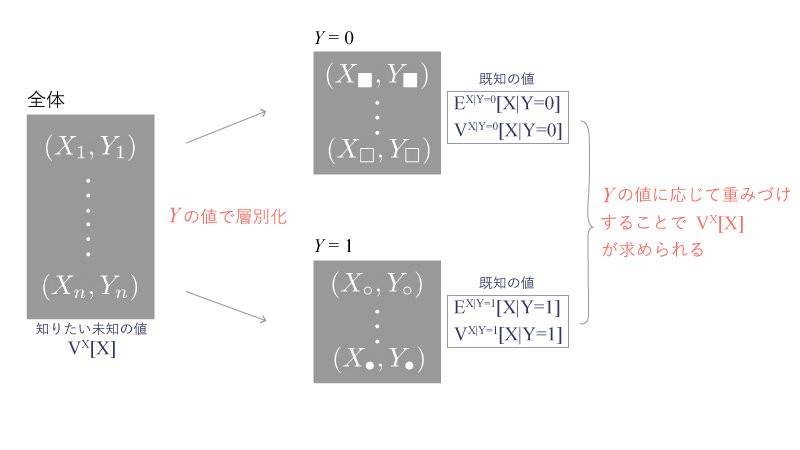
例1, 2とともにこのイメージFigも頭の中にいれておいてください!
1-3. 『分散のくり返しの公式』の証明
(証明)
$X, Y$を確率変数とし、(簡易のために)$E^X[X] = \mu$、とする。
この時、 $$\begin{aligned} V^X[X] &= E^X[(X – \mu)^2] \\ &{\scriptsize (分散の定義より)} \\[5px] &= E^Y[E^{X|Y}[(X – \mu)^2 |Y]] \\ &{\scriptsize (期待値のくり返しの公式より)} \\[5px] &= E^Y[E^{X|Y}[\left\{(X – E^{X|Y}[X|Y]) + (E^{X|Y}[X|Y] – \mu) \right\}^2 |Y]] \\[5px] &= E^Y[E^{X|Y}[\left(X – E^{X|Y}[X|Y] \right)^2 |Y]] \\ &+ E^Y[E^{X|Y}[\left( E^{X|Y}[X|Y] – \mu \right)^2 |Y ]] \\ &+ 2E^Y[E^{X|Y}[\left( X – E^{X|Y}[X|Y] \right) \left( E^{X|Y}[X|Y] – \mu \right) |Y ]] ~~~~~\mathrm{(B)} \end{aligned}$$となり、$$ \begin{aligned} ((B)の1項目) &= E^Y[V^{X|Y}[X|Y]] \\ &{\scriptsize (分散の定義より)}\\[5px] ((B)の2項目) &= E^Y[\left( E^{X|Y}[X|Y] – \mu \right)^2] \\ &= E^Y[\left( E^{X|Y}[X|Y] – E^Y[E^{X|Y}[X|Y]] \right)^2] \\ &{\scriptsize (期待値のくり返しの公式より、\mu = E^X[X] = E^Y[E^{X|Y}[X|Y]])} \\[5px] &= V^Y[E^{X|Y}[X|Y]] \\ &{\scriptsize (分散の定義より)} \\[5px] ((B)の3項目) &= 2E^Y[ \left( E^{X|Y}[X|Y] – \mu \right) \cdot \mathbf{E^{X|Y}\left[\left( X – E^{X|Y}[X|Y] \right) |Y \right]} ] \\ &{\scriptsize (一部を前に出した)} \\[5px] &= 0 \\ &{\scriptsize (太字部分 = E^{X|Y}[X|Y] – E^{X|Y}[X|Y] = 0、より)} \end{aligned}$$ となる。
よって、$$ \begin{aligned} V^X[X] = E^Y[V^{X|Y}[X|Y]] + V^Y[E^{X|Y}[X|Y]] \end{aligned}$$となる。
まとめ.
- 分散のくり返しの公式$$ \begin{aligned} V^X[X] = E^Y[V^{X|Y}[X|Y]] + V^Y[E^{X|Y}[X|Y]] \end{aligned}$$



