$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}}$
今回は「離散分布」に該当する分布を$1$つずつ確認していきます。
【①分布の定義、②確率関数、③特性値、④Fig】を各分布について確認していきましょう!
わかりました!
ところで、分布の種類が多くて$1$つ$1$つ覚えるのが大変ですよね。。。
何か一気に覚える方法はありませんか?
今回扱う分布を一気に覚えるのは難しいですが、分布間の関係性を抑えることで覚えやすくなると思います。
分布間の関係性ですか。。これまであまり意識したことがありませんでした。
それでは分布間の関係性を総括してから$1$つずつ分布を確認しましょう。
0. 離散分布に属する分布間の関係性
離散分布に属する主な分布間の関係性は以下のFig0の通りになっています。
(注意:「離散一様分布」は基本的すぎる分布なので、ここには含めていません)
Fig0.
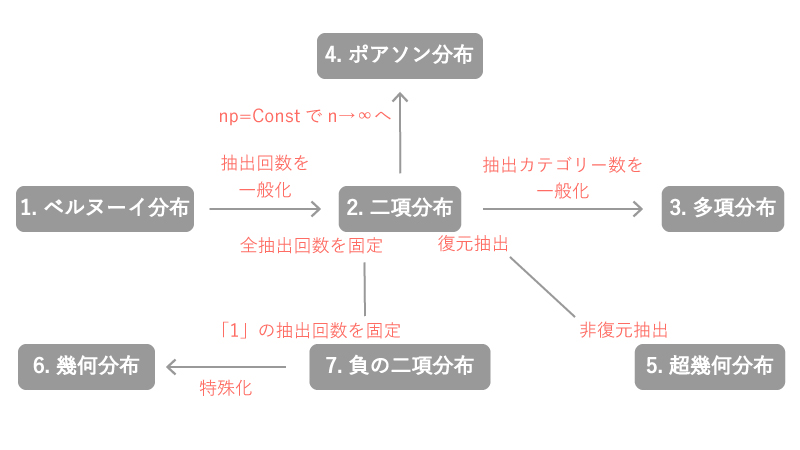
「②二項分布」が様々な分布との関係性をもつので、離散分布の中心に位置するとイメージするとよいかと思います。
以下各分布間の関係性を確認していきます。
0-1. 「①ベルヌーイ分布」と「②二項分布」
ベルヌーイ試行(確率$p ~(0 \leqq p \leqq 1)$で「$1$」を、確率$(1-p)$で「$0$」をとる)を$1$回行った時の「$1$」が出る回数が従う分布が「①ベルヌーイ分布」です。
(試行回数を一般化して)$n$回行った時の「$1$」が出る回数が従う分布が「②二項分布」です。
0-2. 「②二項分布」と「③多項分布」
ベルヌーイ試行(カテゴリー数は「$1$」または「$0$」の$2$個)を$n$回行った時の「$1$」が出る回数が従う分布が「②二項分布」でした。
カテゴリカル試行(カテゴリー数は$K$個。つまりカテゴリー数を一般化したもの。)を$n$回行った時の各カテゴリーの出る回数が従う分布が「③多項分布」です。
0-3. 「②二項分布」と「④ポアソン分布」
ベルヌーイ試行(確率$p ~(0 \leqq p \leqq 1)$で「$1$」を、確率$(1-p)$で「$0$」をとる)を$n$回行った時の「$1$」が出る回数が従う分布が「②二項分布」でした。
「②二項分布」に対して、$np = {\small Const}$の下で$n \to \infty$とした時、「$1$」が出る回数が従う分布が「④ポアソン分布」です。
つまり、「④ポアソン分布」は「②二項分布」に対して(制約条件のもとで)極限をとったものであるとみることができます。
0-4. 「②二項分布」と「⑤超幾何分布」
ベルヌーイ試行(確率$p ~(0 \leqq p \leqq 1)$で「$1$」を、確率$(1-p)$で「$0$」をとる)を$n$回行った時の「$1$」が出る回数が従う分布が「②二項分布」でした。
ところで、箱に入ったカード(「$1$」または「$0$」)の総数を$N$枚、「$1$」の枚数を$M$枚とした時、$n$枚のカードを抽出するとします。(ただし「$1$」の割合を$p$とすると$p = \frac{M}{N}$)
すると、$n$回復元抽出をした時の「$1$」が出る回数は「②二項分布」に従い、 $n$回非復元抽出をした時の「$1$」が出る回数は「⑤超幾何分布」に従います。
0-5. 「②二項分布」と「⑦負の二項分布」
ベルヌーイ試行(確率$p ~(0 \leqq p \leqq 1)$で「$1$」を、確率$(1-p)$で「$0$」をとる)を$n$回行った時の「$1$」が出る回数が従う分布が「②二項分布」でした。
一方で、「$1$」が$r$回抽出された時に全抽出回数が従う分布が「⑦負の二項分布」です。
つまり、「全抽出回数」と「「$1$」の抽出回数」のどちらがfixされているのかの違いです。
0-6. 「⑦負の二項分布」と「⑥幾何分布」
ベルヌーイ試行(確率$p ~(0 \leqq p \leqq 1)$で「$1$」を、確率$(1-p)$で「$0$」をとる)を行い、「$1$」が$r$回抽出された時の全抽出回数が従う分布が「⑦負の二項分布」でした。
(「$1$」の抽出回数を特殊化して)「$1$」が$1$回抽出された時の全抽出回数が従う分布が「⑥幾何分布」です。
- 各分布の定義をご存知ない方は、上記説明がわからないかと思いますので、引き続く各分布の説明を確認した後に再度上記を確認してみてください。
最終的には上記Fig0はすらっと書き下せることが望ましいです。 - 「再生性」という分布(の族)についての性質があります。
「再生性」とは『同じ分布族に含まれる分布に独立に従う$2$つの確率変数に対し、その和が従う分布も同じ分布族に含まれる』という性質です。
「再生性」をもつのは上記Fig中で、
「②二項分布」「③多項分布」「④ポアソン分布」「⑥幾何分布」「⑦負の二項分布」
となります。 - 「無記憶性」という「⑥幾何分布」に特有な性質がありますが、こちらは「6. 幾何分布」で説明します。
少し整理できた気がします!
ここからはいよいよ各分布についてですね。
1. ベルヌーイ分布
1-1. 定義
「確率$p ~(0 \leqq p \leqq 1)$で「$1$」を、確率$(1-p)$で「$0$」をとる確率変数」が従う分布
「確率変数$X$が分布パラメータ$p$のベルヌーイ分布に従うこと」を
「$X \sim \Bern(p)$」と表します。
1-2. 確率関数
$$\begin{aligned} p(x) (= Pr\{ X=x \}) = p^x (1-p)^{1-x} ~~ (x=0, 1) \end{aligned}$$
$p(x) = \begin{cases} 1-p ~~ &(x=0) \\ p ~~ &(x=1) \end{cases}$とも書けますが、上記の方が簡潔ですね。
1-3. 特性値
$$\begin{aligned} &{\small ①平均:}E[X] = p \\ &{\small ②分散:}V[X] = p(1 – p)\\ &{\small ③確率母関数:}G^X(s) = ps + (1 – p) \end{aligned}$$
(①〜③の証明はこちら:<補足. 離散分布_ベルヌーイ分布>)
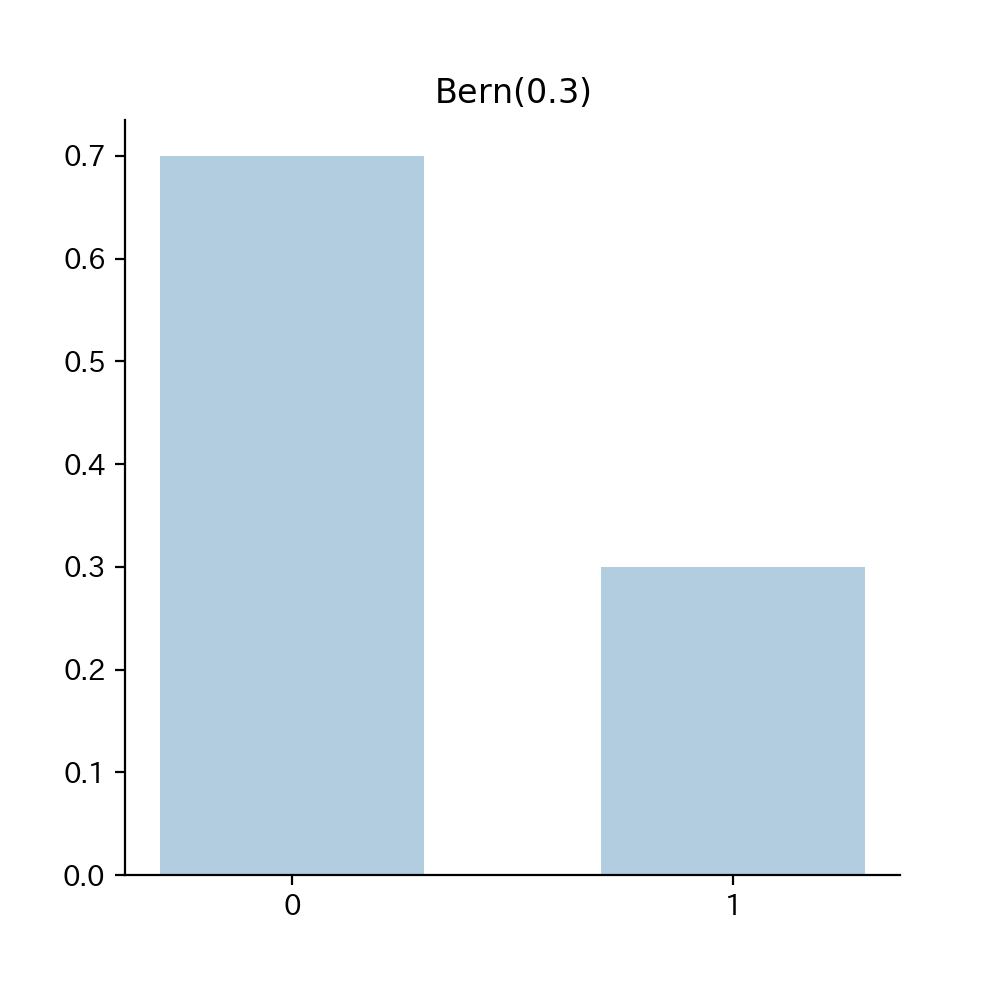
1-4. Fig
Fig1. 確率関数
2. 二項分布
2-1. 定義
『「確率$p ~(0 \leqq p \leqq 1)$で「$1$」を、確率$(1-p)$で「$0$」をとる」というベルヌーイ試行を$n {\small (\in \mathbb{N})}$回行った時に、出た「$1$」の回数(または合計)』が従う分布
「確率変数$X$が分布パラメータ$(n, p)$の二項分布に従うこと」を
「$X \sim \Bin (n, p)$」と表します。
また、ベルヌーイ分布は$\Bin (1, p)$に相当し、二項分布の特殊例です。
2-2. 確率関数
$$\begin{aligned} p(x) (= Pr\{ X=x \}) = \binom{ n }{ x } p^x (1-p)^{n – x} ~~ (x = 0, \ldots, n) \end{aligned}$$
(注意:$\displaystyle \binom{ n }{ x } = \displaystyle {}_n \mathrm{ C }_x$です。本サイトでは$\displaystyle \binom{ n }{ x }$の表記を採用します。)
$p(x)$の”$p^x (1-p)^{n – x}$”は『ある決まった$x$箇所で「$1$」が、残りの$(n-x)$箇所で「$0$」が出る確率』を表し、$p(x)$の”$\displaystyle \binom{ n }{ x }$”は$x$箇所を選ぶ組み合わせを表します。
2-3. 特性値
$$\begin{aligned} &{\small ①平均:}E[X] = np \\ &{\small ②分散:}V[X] = np(1 – p)\\ &{\small ③確率母関数:}G^X(s) = \{ps + (1 – p) \}^n \end{aligned}$$
(①〜③の証明はこちら:<補足. 離散分布_二項分布>)
2-4. Fig
Fig2. 確率関数

3. 多項分布
3-1. 定義
「確率$p_i~(0 \leqq p_i \leqq 1)$」でカテゴリー$i$を選択する$(i = 1, \ldots, K; \sum_{i=1}^K p_i = 1)$」というカテゴリカル試行を$n {\small (\in \mathbb{N})}$回行った時に、選択されたカテゴリー$i$の個数を$X_i$とする。
この時、確率ベクトル$\vec X = (X_1, \ldots, X_K)^\top$が従う分布
「確率ベクトル$\vec X$が分布パラメータ$(n, p_1, \ldots, p_K)$の多項分布に従うこと」を
「$\vec X \sim \Mn (n; p_1, \ldots, p_K)$」と表します。
また、$(X_1, X_2)^\top \sim \Mn (n; p_1, p_2)$である時、$X_1 \sim \Bin (n, p_1)$と同等です。
即ち、二項分布は多項分布の$K=2$の場合に相当し、多項分布の特殊例です。
3-2. 確率関数
$$\begin{aligned} p(\vec x) (&= Pr\{ \vec X= \vec x \} = Pr\{ X_1=x_1, \ldots, X_K=x_K \} ) \\ &= \frac{n!}{x_1! \cdots x_K!} p_1^{x_1} \cdots p_K^{x_K} \end{aligned}$$
$p(x)$の”$p_1^{x_1} \cdots p_K^{x_K}$”は『ある決まった$x_i$箇所でカテゴリー$i$が選択される確率$(i=1, \ldots, K)$』を表し、$p(x)$の”$\dfrac{n!}{x_1! \cdots x_K!}$”は箇所を選ぶ組み合わせを表します。
3-3. 特性値
$$\begin{aligned} &{\small ①平均:}E[X_i] = np_i \\ &{\small ②分散:}V[X_i] = np_i(1 – p_i)\\ &{\small ②’共分散:}\Cov[X_i, X_j] = -n p_i p_j ~~ {\small (ただしi \neq j)} \\ &{\small ③確率母関数:}G^{\vec X}(s_1, \ldots, s_K) (= E[s_1^{X_1} \cdots s_K^{X_K}]) = (p_1 s_1 + \cdots + p_K s_K )^n \end{aligned}$$
(①〜③の証明はこちら:<補足. 離散分布_多項分布>)
多項分布は確率ベクトルを扱うので、必然的に共分散も扱う必要がでてきます。
3-4. Fig
Fig3. 確率関数

- 周辺化(周辺分布)について:
例えば$(X_1, X_2, X_3, X_4, X_5)^\top \sim \Mn (n; p_1, p_2, p_3, p_4, p_5)$である時、
$\vec X_{pre} = (X_1, X_2, n-\sum_{i=1}^2 X_i)^\top, \vec X_{post} = (n-\sum_{i=3}^5 X_i, X_3, X_4, X_5)^\top$とすると、
$$\begin{aligned} \vec X_{pre} &\sim \Mn (n; p_1, p_2, 1- \sum_{i=1}^2 p_i) \\ \vec X_{post} &\sim \Mn (n;1 – \sum_{i=3}^5 p_i, p_3, p_4, p_5) \end{aligned}$$となります。 - 条件づけ(条件づき分布)について:
例えば$(X_1, X_2, X_3, X_4, X_5)^\top \sim \Mn (n; p_1, p_2, p_3, p_4, p_5)$である時、
$\vec X_{pre} = (X_1, X_2)^\top, \vec X_{post} = (X_3, X_4, X_5)^\top$とします。
$1, 2$カテゴリーの合計個数$n_{pre}$、$3, 4, 5$カテゴリーの合計個数$n_{post}$が与えられてる時(即ち、条件づけられている時)、$\vec X_{pre}, \vec X_{post}$は互いに独立で、
$$\begin{aligned} \vec X_{pre} | \sum_{i=1}^2 X_i = n_{pre} &\sim \Mn (n_{pre}; \frac{p_1}{p_{pre}}, \frac{p_2}{p_{pre}}) \\ \vec X_{post} | \sum_{i=3}^5 X_i = n_{post} &\sim \Mn (n_{post}; \frac{p_3}{p_{post}}, \frac{p_4}{p_{post}}, \frac{p_5}{p_{post}}) \end{aligned}$$となります。
(ただし、$p_{pre} = \sum_{i=1}^2 p_i, p_{post} = \sum_{i=3}^5 p_i$)
4. ポアソン分布
4-1. 定義
「単位時間に(各時点でランダムに)平均$\lambda {\small ( \gt 0)}$回生じるイベントが単位時間あたりに生じる合計回数」が従う分布
「確率変数$X$が分布パラメータ$\lambda$のポアソン分布に従うこと」を
「$X \sim \Po (\lambda)$」と表します。
ポアソン分布はなかなかイメージしにくいですよね。。
それでは$1$つ例を挙げてみます。
当時のプロイセン陸軍では『兵士が馬に蹴られて死亡する』というイベントがまれに生じていた様です。この『兵士が馬に蹴られて死亡する』というイベントはランダムに発生していたと考えられますが、$1$年間あたりの同イベント発生数は『イベントが$1$年間あたり平均$0.6$回生じるとした時のポアソン分布(即ち、$\Po (0.6)$)』と非常に類似していた様です。
4-2. 確率関数
$$\begin{aligned} p(x) (= Pr\{ X=x \}) = \frac{e^{- \lambda} \lambda^x}{x!} ~~ (x = 0, 1, \cdots) \end{aligned}$$
ポアソン分布の確率関数は対応する事象から直感的に導くことはできませんが、下のコメント『二項分布との関係性』にある通り、二項分布を利用して導くことができます。
4-3. 特性値
$$\begin{aligned} &{\small ①平均:}E[X] = \lambda \\ &{\small ②分散:}V[X] = \lambda \\ &{\small ③確率母関数:}G^X(s) = \exp[\lambda (s – 1)] \end{aligned}$$
(①〜③の証明はこちら:<補足. 離散分布_ポアソン分布>)
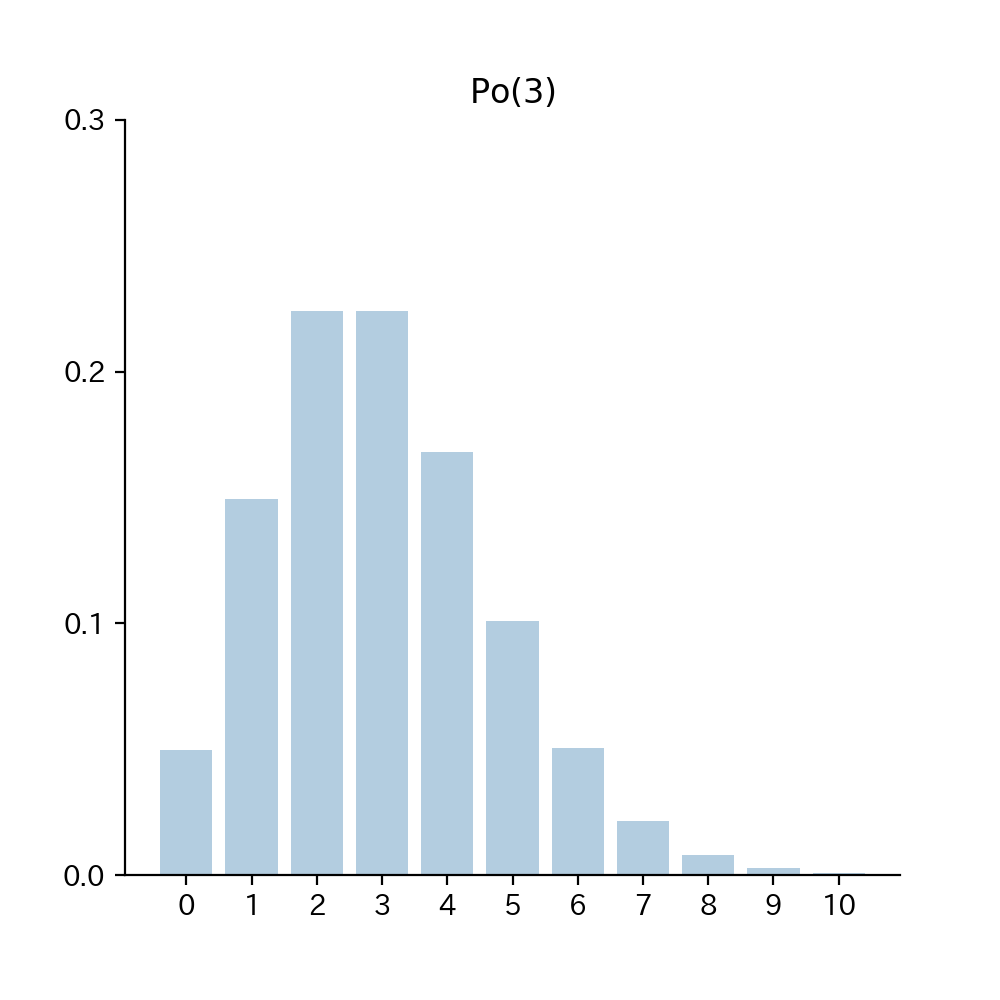
4-4. Fig
Fig4. 確率関数
- 二項分布との関係性:
「二項分布$\Bin (n,p)$に対して$np = \lambda ~ {\small (Const)}$の下で、$n \to \infty$とした時の分布」がポアソン分布$\Po (\lambda)$となっています。
(証明)
二項分布$\Bin (n,p)$に対して$np = \lambda ~ {\small (Const)}$の下で、$n \to \infty$とした時の確率関数が、ポアソン分布$\Po (\lambda)$の確率関数に一致することを示す。
二項分布$\Bin (n, p)$の確率関数$p(x)$について、
$$\begin{aligned} p(x) &= \binom{ n }{ x } p^x (1 – p)^{n – x} \\[10px] &= \binom{ n }{ x } (\frac{\lambda}{n})^x (1 – \frac{\lambda}{n})^{n – x} \\ & {\scriptsize (np=\lambdaより)} \\[10px] &= \frac{n (n-1)\cdots \{ n-(x-1) \}}{x!} \frac{\lambda^x}{n^x} (1 – \frac{\lambda}{n})^{n} (1 – \frac{\lambda}{n})^{-x} \\[10px] &= \frac{\lambda^x}{x!} \cdot 1(1-\frac{1}{n})\cdots(1- \frac{x-1}{n}) \cdot (1 – \frac{\lambda}{n})^{n} (1 – \frac{\lambda}{n})^{-x} \\[10px] &\overset{{n \to \infty}}\longrightarrow \frac{\lambda^x}{x!} \cdot 1(1-0)\cdots(1-0)\cdot e^{- \lambda} (1-0)^{-x} \\ &{\scriptsize ((1 + \frac{x^{\prime}}{n})\overset{{n \to \infty}}\longrightarrow e^{x^{\prime}}より)} \\[10px] &= \frac{\lambda^x e^{-\lambda}}{x!} \end{aligned}$$
これはポアソン分布$\Po (\lambda)$の確率関数に一致していることから、題意は示された。 - 二項分布$\Bin (n,p)$とポアソン分布$\Po (\lambda)$の関係性を示しましたが、いまいちイメージができていない方もいると思いますので、以下具体例を挙げてみます。
(具体例)
ある商品が故障しうり一定間隔で故障してるか確認する、というケースを考えます。
$1$ヶ月(一定間隔)に$\frac{1}{12}$の確率で故障するとすると$1$年での故障回数は$\Bin (12, \frac{1}{12})$に従います。スパンを短くして$1$日を一定間隔とすると故障確率は$\frac{1}{365}$であり、$1$年での故障回数は$\Bin (365, \frac{1}{365})$に従います。さらに一定間隔のスパンを短くしていくと、最終的には各瞬間瞬間で故障してるか確認することになり、これは『各瞬間瞬間で『故障』というイベントがランダムに生じる状況』となります。この最終的な状況において『$1$年での故障回数が従う分布がポアソン分布(今回の例では$\Po(1)$)になるわけです。
5. 超幾何分布
5-1. 定義
「「$1$」または「$0$」が入った箱(合計$N$枚、うち「$1$」は$M$枚)に対して、$n$回の非復元抽出をした時の、「$1$」が出る回数」が従う分布
「確率変数$X$が分布パラメータ$(N, M, n)$の超幾何分布に従うこと」を
「$X \sim \HG (N, M, n)$」と表します。($N, M, n \in \mathbb{N}$)
定義において、『非復元抽出』→『復元抽出』、とした時の「「$1$」が出る回数」が従う分布が二項分布でしたね。
そうですね。同じ箱を用いた復元抽出とすると、二項分布$\Bin (n, p)$の$p$は「$1$」の割合とみれるので$p = \dfrac{M}{N}$であり、$\Bin (n, p) = \Bin (n, \dfrac{M}{N})$となりますね。
5-2. 確率関数
$$\begin{aligned} p(x) (= Pr\{ X=x \}) = \frac{\displaystyle \binom{M}{x} \cdot \binom{N-M}{n-x}}{ \displaystyle \binom{N}{n}} \\\\ ({\small ただし}\max\{ 0, n-(N-M) \} \leqq x \leqq \min\{n, M\}) \end{aligned}$$
$p(x)$の分母は『$N$枚から$n$枚を抽出する組み合わせ』を、
$p(x)$の分子は『「$1$」を抽出する組み合わせ』$\times$『「$0$」を抽出する組み合わせ』を表します。
$x$についての制約条件として、$0 \leqq x \leqq n,~ x \leqq M, ~n-x \leqq N-M$、の$3$つがあるのでこれを整理すると上記の通りになります。
5-3. 特性値
$$\begin{aligned} &{\small ①平均:}E[X] = n(\frac{M}{N}) \\ &{\small ②分散:}V[X] = n(\frac{M}{N})(1 – \frac{M}{N}) \cdot \boldsymbol{\frac{N-n}{N-1}} \\ &{\small ③確率母関数}G^X(s) {\small はきれいな形で書くことができないので、ここでは省きます} \end{aligned}$$
(①〜③の証明はこちら:<補足. 離散分布_超幾何分布>)
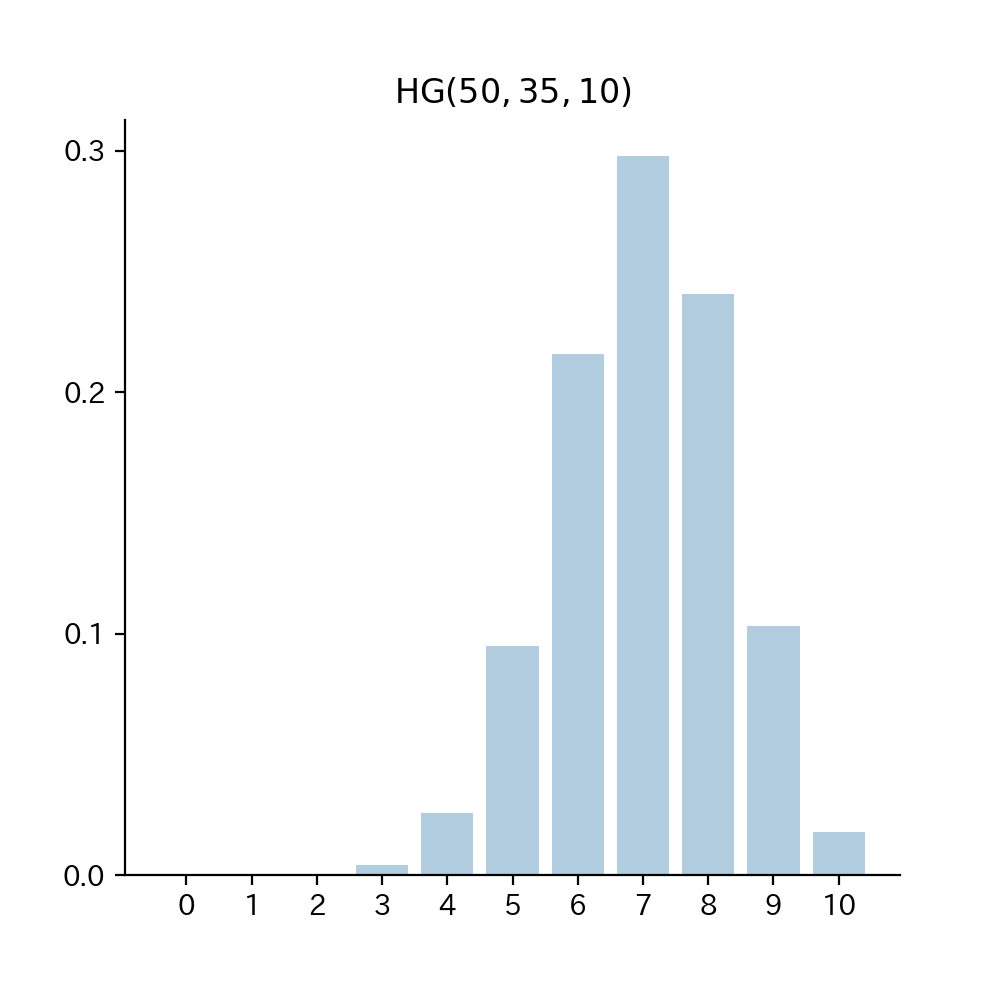
5-4. Fig
Fig5. 確率関数
- $Y \sim \Bin (n, p)$である時、$V[Y] = np(1-p)$、でした。
一方で$p = \dfrac{M}{N}, X \sim \HG (N, M, n)$である時、$V[X] = np(1-p) \cdot \dfrac{N-n}{N-1}$、でした。
両者の差分にあたる$\dfrac{N-n}{N-1}$について、
$$\begin{aligned} \frac{N-n}{N-1} = \frac{1 – \displaystyle \frac{n}{N}}{1 – \displaystyle \frac{1}{N}} \overset{{N \to \infty}}\longrightarrow 1 \end{aligned}$$となり、$N \to \infty$では$V[X]$は$V[Y]$に近づいていきます。
したがって『$N$が十分大きい状況では、非復元抽出は復元抽出と同等』と言うことができます。($N$(合計枚数)が十分大きくなると$1$枚カードを抽出したところで「$1$」の割合はほぼ変化しません)
$N$が十分大きくはない状況(有限)の分散を求める時に、$N$が十分大きい状況(無限)の分散に$\displaystyle \frac{N-n}{N-1}$を乗じる必要があったので、$\displaystyle \frac{N-n}{N-1}$は「有限修正項」と呼ばれます。
6. 幾何分布
6-1. 定義
「割合$p ~(0 \leqq p \leqq 1)$」で「$1$」が、割合$(1-p)$で「$0$」が入った箱から復元抽出をくり返す時、「$1$」が$1$回出るまでの全抽出回数(「$1$」「$0$」の合計枚数)」が従う分布*
(*:上記の『「$1$」「$0$」の合計枚数』部分を『「$0$」の合計枚数』として幾何分布を定義する流派もありますが、本サイトでは上記の流派を採用します)
「確率変数$X$が分布パラメータ$p$の幾何分布に従うこと」を
「$X \sim \Geo(p)$」と表します。
6-2. 確率関数
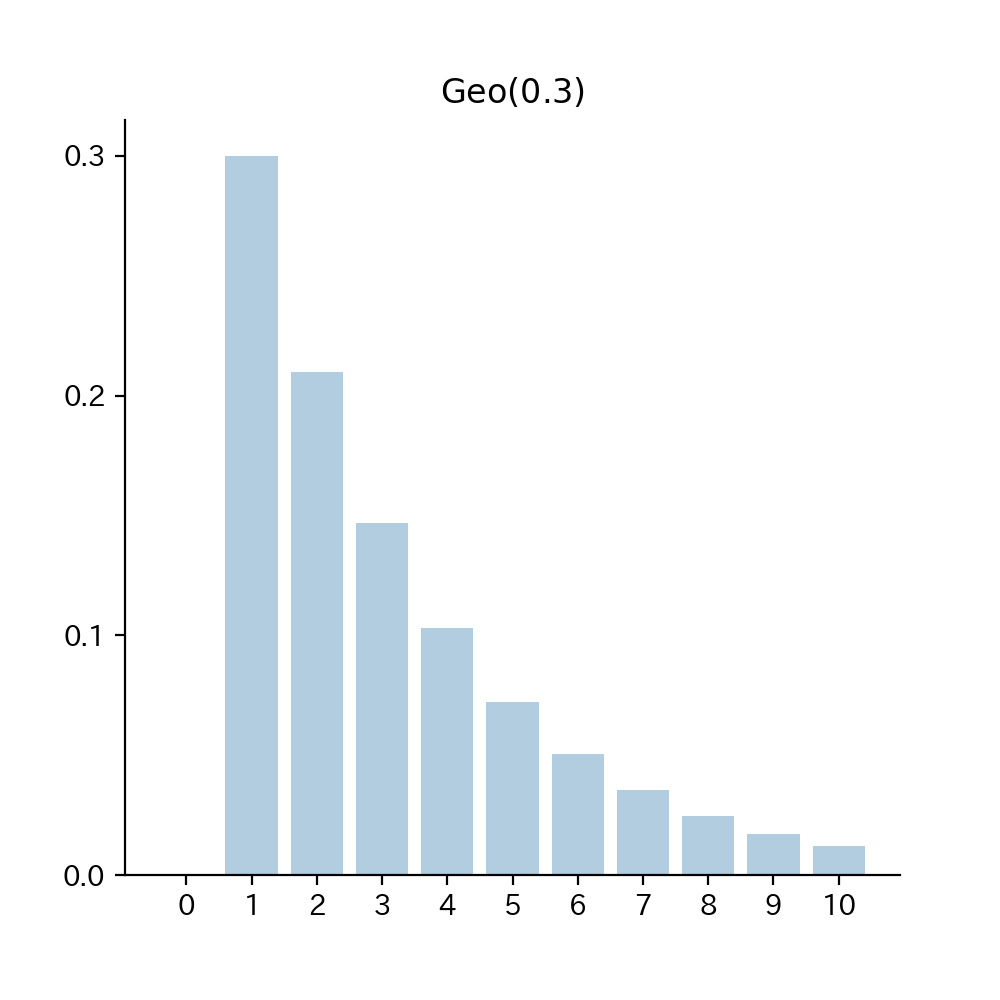
$$\begin{aligned} p(x) (= Pr\{ X=x \}) = p(1-p)^{x-1} ~~ (x=1, 2, \ldots) \end{aligned}$$
$p(x)$の”$(1-p)^{x-1}$”は『$1$回目から$(x-1)$回目まで「$0$」が出る確率』を表し、$p(x)$の”$p$”は『$x$回目で「$1$」が出る確率』を表します。
6-3. 特性値
$$\begin{aligned} &{\small ①平均:}E[X] = \frac{1}{p} \\ &{\small ②分散:}V[X] = \frac{1-p}{p^2} \\ &{\small ③確率母関数:}G^X(s) = \frac{ps}{1-(1-p)s} ~~ {\small (ただし|(1-p)s| \lt 1)} \end{aligned}$$
(①〜③の証明はこちら:<補足. 離散分布_幾何分布>)
6-4. Fig
Fig6. 確率関数
- (幾何分布の)無記憶性:
$X \sim \Geo(p)$である時、
$$\begin{aligned} Pr\{ X \geqq n_1 + n_2 | X \geqq n_1 \} = Pr\{ X \geqq n_2 \} \end{aligned}$$が成立し、これを「(幾何分布の)無記憶性」と言います。
(証明)
$$\begin{aligned} Pr\{ X \geqq n_1 + n_2 | X \geqq n_1 \} = \frac{(1-p)^{n_1 + n_2}}{(1-p)^{n_1}} = (1-p)^{n_2} \end{aligned}$$であり、一方で、
$$\begin{aligned} Pr\{ X \geqq n_2 \} = (1-p)^{n_2} \end{aligned}$$である。
よって、題意は示された。
「無記憶性」についての具体例として、スロットで当たりが出るまでにスロットを回す回数を考えてみます。
$100$回回して当たりがでなかった人の気持ちとしては『$100$回も回したんだからそろそろ当たりは出るだろう』となるかもしれませんが、回し始めた時点($0$回回した後)と当たりがでる確率は同じ(分布は同じ)です。
7. 負の二項分布
7-1. 定義
「割合$p ~(0 \leqq p \leqq 1)$」で「$1$」が、割合$(1-p)$で「$0$」が入った箱から復元抽出をくり返す時、「$1$」が$r {\small (\in \mathbb{N})}$回出るまでの全抽出回数(「$1$」「$0$」の合計枚数)」が従う分布*
(*:上記の『「$1$」「$0$」の合計枚数』部分を『「$0$」の合計枚数』として負の二項分布を定義する流派もありますが、本サイトでは上記の流派を採用します)
「確率変数$X$が分布パラメータ$(r, p)$の負の二項分布に従うこと」を
「$X \sim \NB (r, p)$」と表します。
幾何分布$\Geo(p)$は$\NB (1, p)$に相当し、負の二項分布の特殊例であることがわかります。
7-2. 確率関数
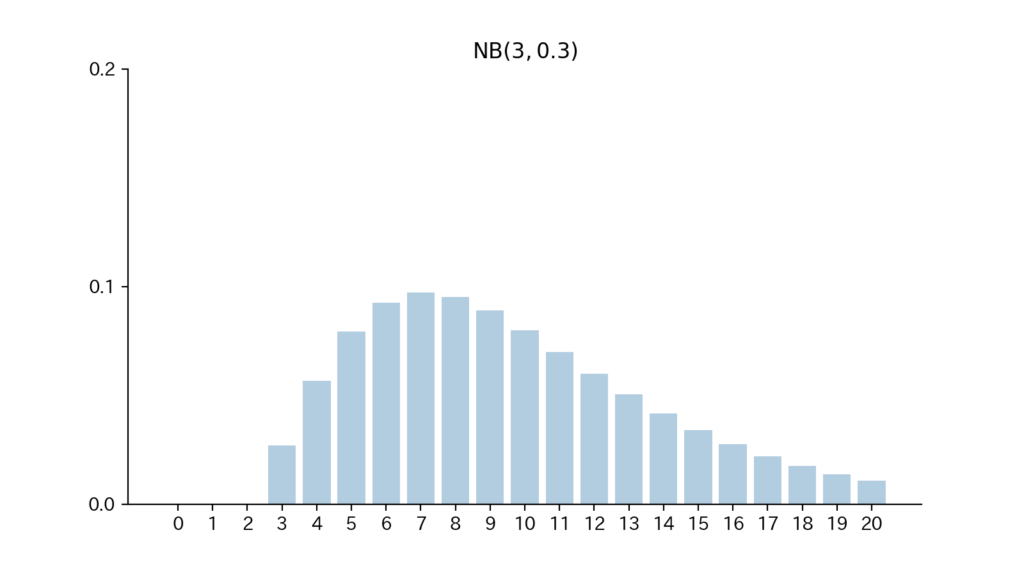
$$\begin{aligned} p(x) (= Pr\{ X=x \}) &= \binom{x-1}{r-1} p^{r-1} (1-p)^{x-r} p ~~~~~ \mathrm{(A)} \\ &= \binom{x-1}{r-1} p^r (1-p)^{x-r} ~~ {\small (x=r, r+1, \ldots)} \end{aligned}$$
$\mathrm{(A)}$の”$p^{r-1} (1-p)^{x-r}$”は『$1$回目から$(x-1)$回目までの決まった$(x-r)$箇所で「$0$」が、残りの$(r-1)$箇所で「$1$」が出る確率』を、$p(x)$の”$p$”は『$x$回目で「$1$」が出る確率』を、$p(x)$の”$\displaystyle \binom{x-1}{r-1}$”は箇所を選ぶ組み合わせを表します。
7-3. 特性値
$$\begin{aligned} &{\small ①平均:}E[X] = \frac{r}{p} \\ &{\small ②分散:}V[X] = \frac{(1-p)r}{p^2} \\ &{\small ③確率母関数:}G^X(s) = \left\{\frac{ps}{1-(1-p)s} \right\}^r ~~ {\small (ただし|(1-p)s| \lt 1)} \end{aligned}$$
(①〜③の証明はこちら:<補足. 離散分布_負の二項分布>)
7-4. Fig
Fig7. 確率関数
まとめ.
- 離散分布に属する分布間の関係性を確認し、各分布について【①分布の定義、②確率関数、③特性値、④Fig】を確認した。








