$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}} \\ \gdef \tr {\mathrm{tr}}$
重回帰モデルの回帰係数の検定には$\F$検定が用いられます。
$\F$検定は$\F$分布(参照:<連続分布>)に基づく検定です。
重回帰モデルでは回帰係数が複数個出てくると思いますが、帰無仮説$H_0$の置き方はどの様になりますか?
絶対的なものがあるわけではありませんが、統計ソフトでよく採用されているのは「$\beta_2 = \cdots = \beta_d = 0$(ただし$\beta_1$が切片項とした重回帰モデル)」や「$\beta_k=0$」といったものです。
よくある流れとしては、「$\beta_2 = \cdots = \beta_d = 0$(ただし$\beta_1$が切片項とした重回帰モデル)」という帰無仮説が棄却されれば、次に「$\beta_k=0$」という帰無仮説を検定する、といったものでしたね。
1. $\F$検定
確率変数$X_1, X_2$が
$$\begin{aligned} X_1 \sim \chi^2(n_1) \\ X_2 \sim \chi^2(n_2) \end{aligned}$$で互いに独立である時、
$$\begin{aligned} X = \frac{\frac{X_1}{n_1}}{\frac{X_2}{n_2}} \sim \F(n_1, n_2) \end{aligned}$$が成立しました。
(参照:<連続分布>:「9. $F$分布」)
ある統計量$\F$が(上記$X$の様に)$\F$分布に従う時、それを$\boldsymbol{\F}$統計量($\F$検定統計量)」と言い、それに基づく検定を「$\boldsymbol{\F}$検定」と言います。
2. 重回帰モデルにおける$\F$検定
目的変数$y_i$、説明変数$x_{i,1}, \cdots, x_{i,d} ~~ (i=1, \cdots, n)$に対して、
$$\begin{aligned} &\begin{cases} y_i &= \beta_1 x_{i,1} + \cdots + \beta_d x_{i,d} + \varepsilon_i \\ \varepsilon_i &\overset{i.i.d}\sim \N(0, \sigma^2) \end{cases} \\[20px] \iff &\begin{cases} \vec y &= \vec X \vec \beta + \vec \varepsilon \\ \vec \varepsilon &\sim \N(\vec 0, \sigma^2 I_n) \end{cases} \end{aligned}$$という重回帰モデルを考えます。
ただし、
$$\begin{aligned} \vec X &= \begin{pmatrix} x_{1,1} &\cdots &x_{1,d} \\ \vdots &\ddots &\vdots \\ x_{n,1} &\cdots &x_{n,d} \end{pmatrix} ~~ (\in \mathbb{R}^{n \times d}) \\ \vec y &= (y_1, \cdots, y_n)^{\top} ~~ (\in \mathbb{R}^{n}) \\ \vec \beta &= (\beta_1, \cdots, \beta_d)^{\top} ~~ (\in \mathbb{R}^{d}) \\ \vec \varepsilon &= (\varepsilon_1, \cdots, \varepsilon_n)^{\top} ~~ (\in \mathbb{R}^{n}) \end{aligned}$$とします。
切片項を置きたい場合には、$(x_{1,1}, \ldots, x_{n,1})^{\top} = \vec 1$、としてください。この時、$y_i = \beta_1 + \beta_2 x_{i,2} \cdots + \beta_d x_{i,d} + \varepsilon_i$、というモデルになっています。「2. 重回帰モデルにおける$F$検定」においては、切片項を置く置かないに関わらず話は同じです。ただし、「3. 重回帰モデルにおける回帰係数の検定の流れ」では切片項を置く置かないによって帰無仮説の設定が一部変わってきます。
重回帰モデルにおける回帰ベクトル$\vec \beta (\in \mathbb{R}^{d})$の検定の一般形として、
$$\begin{aligned} \begin{cases} {\small 帰無仮説} H_0: \vec \beta \in \Theta_0 \\ {\small 帰無仮説} H_1: \vec \beta \in \mathbb{R}^{d} \backslash \Theta_0 \end{cases} \end{aligned}$$という有意水準$\alpha$の検定を考えます。
(ただし、$\Theta_0$は$\mathbb{R}^{d}$内の(線形)部分空間、$\mathbb{R}^{d} \backslash \Theta_0$は$\mathbb{R}^{d}$内の$\Theta_0$を除く空間であり、$\color{red}{dim \Theta_0 = r}$$~~(<d)$とします)
もともと$\vec \beta$は自由度$d$ですが、帰無仮説$\Theta_0$では自由度が$r$となっています。これは$\beta_2 = 0$の様な制約条件がかされたことで自由度が減ったというイメージです。
帰無仮説$H_0$、フルモデル、の下での残差ベクトルの$2$乗和$R_0^2, R_1^2$は、
$$\begin{aligned} R_0^2 &= \underset{\vec \beta \in \Theta_0}{\min} \| \vec y-\vec X \vec \beta \|^2 \\ R_1^2 &= \underset{\vec \beta \in \color{red}{\mathbb{R}^{d}}}{\min} \| \vec y-\vec X \vec \beta \|^2 \end{aligned}$$となりますが、$R_0^2 >> R_1^2$、であれば帰無仮説$H_0$を棄却(対立仮説$H_1$を選択)するのが妥当です。
一般に、制約条件がつかないモデルを『フルモデル』と言います。
ここでは帰無仮説$H_0$、フルモデル、の下での残差ベクトルの$2$乗和$R_0^2, R_1^2$の大小を比較することでどちらの仮説を選択すべきか判断しました。
$\F$検定において$R_0^2, R_1^2$の大小を比較する時には、帰無仮説$H_0$が正しいという仮定の下で、
$$\begin{aligned} \F = \frac{\frac{R_0^2-R_1^2}{\color{red}{d-r}}}{\frac{R_1^2}{\color{red}{n-d}}} \sim \F(\textcolor{red}{d-r}, \textcolor{red}{n-d}) ~~~~~ \mathrm{(A)} \end{aligned}$$であること*を利用して、
⚫︎$\F \leqq \F_{\alpha}(d-r, n-d) \Rightarrow {\small H_0を選択}$
⚫︎$\F \gt \F_{\alpha}(d-r, n-d) \Rightarrow {\small H_1を選択}$
となります。
(補足)
*:ある事実とFigとを用いて説明します。
(初見の場合には難しいかもしれないので、飛ばしていただいても結構です)
(事実ここから)
①$\vec z \sim \N_n(\vec 0, I_n)$である時、
$$\begin{aligned} (\| \vec z \|^2=) ~~ \vec z^{\top} \vec z \sim \chi^2(n) \end{aligned}$$
②$A$を$a$次元空間への直交射影行列とする時、
$$\begin{aligned} (&\| A^{\top} \vec z \|^2 = \\[10px] &\vec z^{\top} A A^{\top} \vec z =) \\[10px] &\vec z^{\top} A \vec z \sim \chi^2(a) \\ &{\scriptsize (直交射影行列の性質よりA^{\top} = A, A^2 = A)} \end{aligned}$$
③$I-A$は$(n-a)$次元空間への直交射影行列となるから、
$$\begin{aligned} (&\| (I-A)^{\top} \vec z \|^2 = \\[10px] &\vec z^{\top} (I-A) (I-A)^{\top} \vec z =) \\[10px] &\vec z^{\top} (I-A) \vec z \sim \chi^2(n-a) \\ &{\scriptsize ((I-A)も直交行列であり上記と同様)} \end{aligned}$$
④$\vec z^{\top} A \vec z$と$\vec z^{\top} (I-A) \vec z$とはそれぞれ独立
(直交射影行列については<最小$2$乗法>を参照)
①〜④をまとめると、
『
$\vec z \sim \N_n(\vec 0, I_n)$である時、$\vec z^{\top} \vec z = \vec z^{\top} A \vec z + \vec z^{\top} (I-A) \vec z$、と分解され(三平方の定理の形)、
$\rank A = a$であれば、
$$\begin{aligned} \vec z^{\top} A \vec z &\sim \chi^2(a) \\[10px] \vec z^{\top} (I-A) \vec z &\sim \chi^2(n-a) \end{aligned}$$と$\chi^2$成分が分解され、それぞれ独立となる。
』
(事実ここまで)
それでは以下Fig1の通り、$\vec z = \frac{\vec y-\vec X \vec \beta}{\sigma}$とおいて、その射影を考えてみましょう。
ここではモデル空間$M(\in \mathbb{R}^{d})$を平面に、帰無仮説$H_0$のモデル空間$\Theta_0($$\Theta_0$は$\mathbb{R}^{d}$内の(線形)部分空間$)$を直線とみなしています。
Fig1.
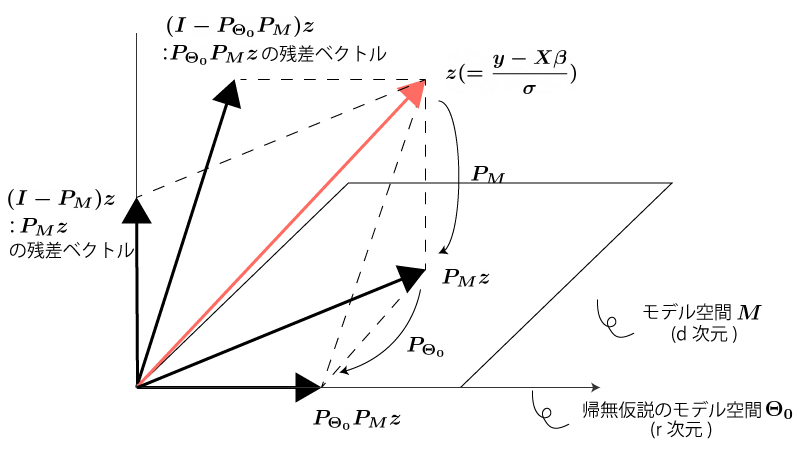
上記事実と、$P_M$が$d$次元空間への直交射影行列であることから、 $\vec z$を$P_M \vec z, (I-P_M) \vec z$に分解する場合を考えると、
$$\begin{aligned} \| \vec z\|^2 &= \| P_M \vec z \|^2 + \| (I-P_M) \vec z\|^2 \\[10px] \Rightarrow \underbrace{\vec z^{\top} \vec z}_{\sim \chi^2(n)} &= \underbrace{\vec z^{\top} P_M \vec z}_{\sim \chi^2(d)} + \underbrace{\vec z^{\top} (I-P_M) \vec z}_{\sim \chi^2(n-d)} \end{aligned}$$となる。
また、上記事実と、$P_{\Theta_0} P_M (=P_{\Theta_0})$*が$r$次元空間への直交射影行列であることから、 $\vec z$を$P_{\Theta_0} P_M \vec z, (I-P_{\Theta_0} P_M) \vec z$に分解する場合を考えると、
$$\begin{aligned} \| \vec z\|^2 &= \| P_{\Theta_0} P_M \vec z \|^2 + \| (I-P_{\Theta_0} P_M) \vec z \|^2 \\[10px] \Rightarrow \underbrace{\vec z^{\top} \vec z}_{\sim \chi^2(n)} &= \underbrace{\vec z^{\top} P_{\Theta_0} P_M \vec z}_{\sim \chi^2(r)} + \underbrace{\vec z^{\top} (I-P_{\Theta_0} P_M) \vec z}_{\sim \chi^2(n-r)} \\[10px] (\Rightarrow \underbrace{\vec z^{\top} \vec z}_{\sim \chi^2(n)} &= \underbrace{\vec z^{\top} P_{\Theta_0} \vec z}_{\sim \chi^2(r)} + \underbrace{\vec z^{\top} (I-P_{\Theta_0}) \vec z}_{\sim \chi^2(n-r)}) \end{aligned}$$となります。
*の$P_{\Theta_0} P_M =P_{\Theta_0}$について補足します。
$P_{\Theta_0} P_M$は『モデル空間$M$に直交射影してから帰無仮説のモデル空間$\Theta_0$に直交射影すること』を、$P_{\Theta_0}$は『帰無仮説のモデル空間$\Theta_0$に直交射影すること』を表すことから、Fig2を参照すると両者が等しいことが直観的にわかります。(証明は難しくないですがここでは割愛します)
以上より、Fig2の通りになります。
Fig2.
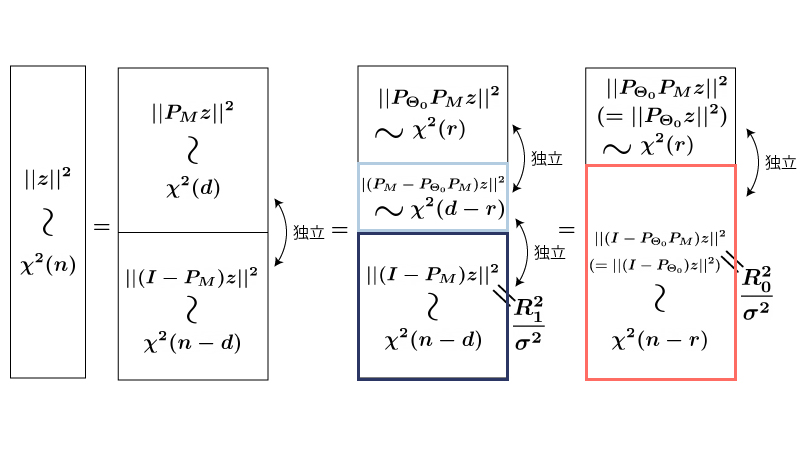
Fig2内部の$\frac{R_1^2}{\sigma^2}, \frac{R_0^2}{\sigma^2}$部分について補足します。
$(I-P_M) \vec z, (I-P_{\Theta_0} ) \vec z$について、
$$\begin{aligned} (I-P_M) \vec z &= \frac{\vec y-\vec X \vec \beta-P_M(\vec y-\vec X \vec \beta)}{\sigma} \\ &= \frac{\vec y-\vec X \vec \beta-\hat{\vec y} + \vec X \vec \beta}{\sigma} \\ &{\scriptsize(\hat{\vec y}=P_M \vec yとした。\vec X \vec \beta \in MよりP_M \vec X \vec \beta = \vec X \vec \beta)} \\ &= \frac{\vec y-\hat{\vec y}}{\sigma} \\[20px] (I-P_{\Theta_0} ) \vec z &= \frac{\vec y-\vec X \vec \beta-P_{\Theta_0}(\vec y-\vec X \vec \beta)}{\sigma} \\ &= \frac{\vec y-\vec X \vec \beta-\tilde{\vec y} + \vec X \vec \beta}{\sigma} \\ &{\scriptsize(\tilde{\vec y}=P_{\Theta_0} \vec yとした。\color{red}{帰無仮説H_0が正しい時}\vec X \vec \beta \in \Theta_0よりP_{\Theta_0} \vec X \vec \beta = \vec X \vec \beta}{\scriptsize)} \\ &= \frac{\vec y-\tilde{\vec y}}{\sigma} \end{aligned}$$であることから、
$$\begin{aligned} \| (I-P_M) \vec z \|^2 &= \frac{R_1^2}{\sigma^2} \\ \| (I-P_{\Theta_0}) \vec z \|^2 &= \frac{R_0^2}{\sigma^2} \end{aligned}$$となっています。
(独立な)濃い青領域と薄い青領域に注目すると$\mathrm{(A)}$が導かれます。
濃い青領域と赤領域に注目するとどうでしょうか?
濃い青領域と赤領域は独立ではないので$\mathrm{(A)}$の様な形を導くことはできません。
例1.
目的変数$y_i$、説明変数$x_{i,1}, x_{i,2}, x_{i,3}, x_{i,4} ~~ (i=1, \cdots, n)$に対して、
$$\begin{aligned} \begin{cases} y_i &= \beta_1 x_{i,1} + \beta_2 x_{i,2} + \beta_3 x_{i,3} + \beta_4 x_{i,4} + \varepsilon_i \\ \varepsilon_i &\overset{i.i.d}\sim \N(0, \sigma^2) \end{cases} \end{aligned}$$という重回帰モデルを考える。
ただし、$x_{i,1} = 1 ~~ (i=1, \cdots, n)$とする。
この時、回帰係数ベクトル$\vec \beta = (\beta_1, \beta_2, \beta_3, \beta_4)$に対して、
⚫︎${\small 帰無仮説} H_0: \vec \beta \in \Theta_0$
(ただし、$\Theta_0 = \{ \vec \beta \in \mathbb{R}^4 | \beta_3 = 0 \}$)
⚫︎${\small 対立仮説} H_1: \vec \beta \in \mathbb{R}^{d} \backslash \Theta_0$
という有意水準$\alpha$の検定を考える。
帰無仮説$H_0$、フルモデルの下での残差ベクトルの$2$乗和$R_0^2, R_1^2$は、
$$\begin{aligned} R_0^2 &= \underset{\vec \beta \in \Theta_0}{\min} \| \vec y-\vec X \vec \beta \|^2 \\ R_1^2 &= \underset{\vec \beta \in \color{red}{\mathbb{R}^{4}}}{\min} \| \vec y-\vec X \vec \beta \|^2 \end{aligned}$$であり、帰無仮説$H_0$、フルモデルの下での$\vec \beta$の自由度はそれぞれ$3$、$4$であるから、 帰無仮説$H_0$が正しいという仮定の下で、
$$\begin{aligned} \F = \frac{\frac{R_0^2-R_1^2}{1}}{\frac{R_1^2}{n-4}} \sim \F(1, n-4) \end{aligned}$$となる。
よって、
⚫︎$\F \leqq \F_{\alpha}(1, n-4) \Rightarrow {\small H_0を選択}$
⚫︎$\F \gt \F_{\alpha}(1, n-4) \Rightarrow {\small H_1を選択}$
となる。
3. 重回帰モデルにおける回帰係数の検定の流れ
目的変数$y_i$、説明変数$x_{i,1},\cdots, x_{i,d} ~~ (i=1, \cdots, n)$に対して、
$$\begin{aligned} \begin{cases} y_i &= \beta_1 x_{i,1} + \cdots + \beta_d x_{i,d} + \varepsilon_i \\ \varepsilon_i &\overset{i.i.d}\sim \N(0, \sigma^2) \end{cases} \end{aligned}$$という重回帰モデルを考えます。
ただしモデルには切片項$\beta_1$があるものとして、$(x_{1,1}, \cdots, x_{n,1})^{\top} = \vec 1$、とします。
この重回帰モデルにおける、よくある*回帰係数の検定の流れは以下の通りとなります。
(*:一般の統計ソフトで出力されるものを想定しています)
step1)『重回帰モデルが最低限のモデルとして成立しているか?』の検定
⚫︎${\small 帰無仮説}: \beta_{\color{red}{2}} = \cdots = \beta_d = 0$
を考え、これを棄却できれば(対立仮説が選択されれば)step2に進みます。
帰無仮説を棄却できない場合にはstep2には進まず終了です。
$\beta_{\color{red}{2}} = \cdots = \beta_d = 0$である時、モデルは$y_i = \beta_1$となります。このモデルでは流石に説明が厳しいとなった場合にstep2に進むのですね。
step2)各回帰係数の検定
個々の$\beta_i ~~ (i=\textcolor{red}{1},2, \cdots, n)$に対して、
⚫︎${\small 帰無仮説}: \beta_i = 0$
を考え、検定をします。
一般の統計ソフトで重回帰モデルの回帰係数の検定をする時、step1, step2の結果が一気に表示されるはずです。なお、step1, step2において具体的にどのような$\F$検定が行われているかについてはやや難しいので、興味のある方は<補足. F検定_回帰係数の検定>を参照してください。
まとめ.
- 重回帰モデルの回帰係数の検定に用いられる$\F$検定を紹介した。
- stepごとにどのような帰無仮説が置かれるのか?、(余裕があれば)stepごとにどのような検定が行われるのかをおさえておく。







