最小2乗法

（補足1）

誤差項に正規性の仮定を置いた場合には、最小$2$乗推定量$\hat{\vec \beta}$と最尤推定量$\check{\vec \beta}$は一致します。
以下それを説明します。


誤差項に正規性の仮定を置いた場合には$y_i \sim \N(\beta_1 x_{i,1} + \cdots + \beta_d x_{i,d}, \sigma^2)$であるから、尤度関数$L(\vec \beta, \sigma^2)$は、
$$\begin{aligned} L(\vec \beta, \sigma^2) &= \prod_{i=1}^{n} \frac{1}{\sqrt {2 \pi \sigma^2}} \exp(-\frac{\{ y_i-(\beta_1 x_{i,1} + \cdots + \beta_d x_{i,d}) \}^2}{2 \sigma^2}) \\ &{\scriptsize (y_i ~~ (i=1, \cdots, n)の独立性より)} \\[10px] &= \frac{1}{(2 \pi \sigma^2)^{\frac{n}{2}}} \exp(-\frac{1}{2 \sigma^2} \sum_{i=1}^{n} \{ y_i-(\beta_1 x_{i,1} + \cdots + \beta_d x_{i,d}) \}^2 ) \\[10px] &= \frac{1}{(2 \pi \sigma^2)^{\frac{n}{2}}} \exp(-\frac{1}{2 \sigma^2} || \vec y-\vec X \vec \beta ||^2) ~~~~~ \mathrm{(J)} \end{aligned}$$となります。


$\mathrm{(J)}$を最大化する$\vec \beta$の推定量が最尤推定量$\check{\vec \beta}$であり、$\mathrm{(J)}$内の$|| \vec y-\vec X \vec \beta ||^2$を最小化する$\vec \beta$の推定量が最小$2$乗推定量$\hat{\vec \beta}$でした。$\mathrm{(J)}$の最大化、$\mathrm{(J)}$内の$|| \vec y-\vec X \vec \beta ||^2$の最小化、は同じことを指すので、最小$2$乗推定量$\hat{\vec \beta}$と最尤推定量$\check{\vec \beta}$は一致します。

（補足2）

$P_X = \vec X (\vec X^{\top} \vec X)^{-1} \vec X^{\top}$に対して、

①$P_{X}^2 = P_{X}$
②$P_{X}^{\top} = P_{X}$
③$P_{X} \vec X = \vec X$
④$P_{X} \vec a \in Im(\vec X) ~~ (\forall a \in \mathbb{R}^{n})$

（ただし、$Im(\vec X)$は$\vec X$の列ベクトルで張られた空間）

が成立します。
証明は＜補足. 最小$2$乗法_$P_{X}$についての性質の証明＞を参照してください。

（補足3）

最小$2$乗法の幾何的なイメージを確認してみましょう。
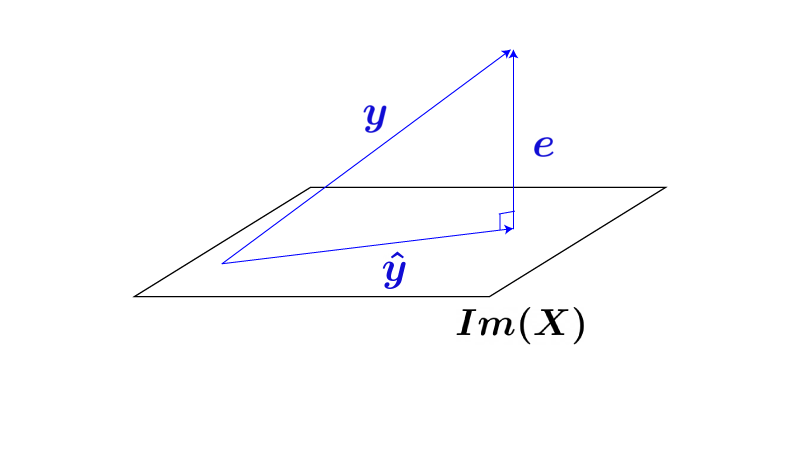
残差ベクトル$\vec e$と最小$2$乗推定量$\hat{\vec y}$の内積$\left< \vec e, \hat{\vec y} \right>$は、
$$\begin{aligned} \left< \vec e, \hat{\vec y} \right> &= \vec e^{\top} \hat{\vec y} \\[10px] &= ((I_n-P_X) \vec y)^{\top} P_X \vec y \\[10px] &= \vec y^{\top} (I_n-P_X)^{\top} P_X \vec y \\[10px] &= \vec y^{\top} (I_n-P_X^{\top}) P_X \vec y \\ &{\scriptsize (I_n^{\top} = I_n)} \\[10px] &= \vec y^{\top} (I_n-P_X) P_X \vec y \\ &{\scriptsize (P_Xの性質②より)} \\[10px] &= \vec y^{\top} (P_X-P_X^2) \vec y \\[10px] &= \vec y^{\top} (P_X-P_X) \vec y \\ &{\scriptsize (P_Xの性質①より)} \\[10px] &= 0 \end{aligned}$$となるため、残差ベクトル$\vec e$と最小$2$乗推定量$\hat{\vec y}$は直交することがわかります。


よってベクトルの位置関係としてはFig1の様になり、$\vec y$から$\hat{\vec y}$を求めることは$\vec y$を$Im(\vec X)$に直交射影することに他ならない、とわかります。
（$P_X$は「直交射影行列*」の1つです）


Fig1.

*：直交射影行列についての補足
一般に、正方行列$P$が、

①’$P^2 = P$
②’$P^{\top} = P$

の2つを満たす時、$P$は直交射影行列となります。


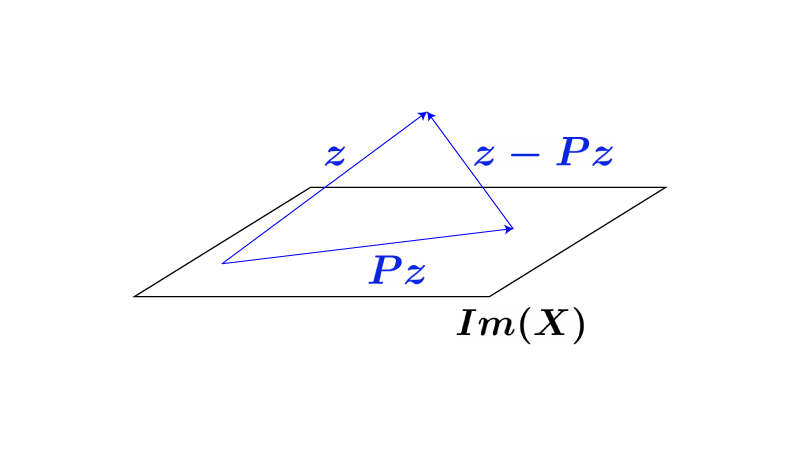
なぜなら、 ①’は『くり返し$P$を作用させても結果がかわらない』ことを意味し、それは『$P$が射影行列である』ことと同義であり、また、
$$\begin{aligned} \left< \vec z-P \vec z, P \vec z \right> &= (\vec z-P \vec z)^{\top} P \vec z \\[10px] &= \vec z^{\top} P \vec z-\vec z^{\top} P^{\top} P \vec z \\[10px] &= \vec z^{\top} P \vec z-\vec z^{\top} P^2 \vec z \\ &{\scriptsize (P_Xの性質②よりP^{\top}=P)} \\[10px] &= \vec z^{\top} P \vec z-\vec z^{\top} P \vec z \\ &{\scriptsize (P_Xの性質①りP^{2}=P)} \\[10px] &= 0 \end{aligned}$$となるため、$\vec z-P \vec z$と$P \vec z$は直交するためです。
（$\vec z-P \vec z$と$P \vec z$の位置関係は以下Fig2を参照してください）

Fig2.（本来$\vec z-P \vec z$と$P \vec z$は直交しますが、上記確認前は両者が直交することがわかっていないので、あえて直交しないかのごとく描いています）

すたどく

$P_X$では①〜④が成立しましたが、一般の直交射影行列では③④は必ずしも成立しません。

（補足4）

最小$2$乗法により最小$2$乗推定量$\hat{\vec \beta}$が求まりましたが、$\sigma^2$の推定量はまだ求まっていません。
（最小$2$乗法は$\sigma^2$の推定量を与えません）


そこで、以下では$\sigma^2$の不偏推定量を求めてみます。


（天下り的ですが）$|| \vec e ||^2$は、
$$\begin{aligned} || \vec e ||^2 &= || \vec y-\hat{\vec y} ||^2 \\[10px] &= || (I_n-P_X) \vec y ||^2 \\[10px] &= || (I_n-P_X)(\vec X \vec \beta + \vec \varepsilon) ||^2 \\[10px] &= \{ (I_n-P_X)(\vec X \vec \beta + \vec \varepsilon) \}^{\top} \{ (I_n-P_X)(\vec X \vec \beta + \vec \varepsilon) \} \\[10px] &= \{ \vec X \vec \beta + \vec \varepsilon-P_X \vec X \vec \beta-P_X \vec \varepsilon \}^{\top} \{ \vec X \vec \beta + \vec \varepsilon-P_X \vec X \vec \beta-P_X \vec \varepsilon \} \\[10px] &= \{ (I_n-P_X) \vec \varepsilon \}^{\top} \{ (I_n-P_X) \vec \varepsilon \} \\ &{\scriptsize (P_X \vec X \vec \beta = \vec X \vec \beta)} \\[10px] &= \vec \varepsilon^{\top} (I_n-P_X)^{\top} (I_n-P_X) \vec \varepsilon \\[10px] &= \vec \varepsilon^{\top} (I_n^{\top}-P_X^{\top}) (I_n-P_X) \vec \varepsilon \\[10px] &= \vec \varepsilon^{\top} (I_n-P_X) (I_n-P_X) \vec \varepsilon \\ &{\scriptsize (I_n^{\top} = I_n, P_X^{\top} = P_X)} \\[10px] &= \vec \varepsilon^{\top} (I_n^2-P_X-P_X + P_X^2) \vec \varepsilon \\[10px] &= \vec \varepsilon^{\top} (I_n-P_X) \vec \varepsilon \\ &{\scriptsize (I_n^2 = I_n, P_X^2 = P_X)} \end{aligned}$$となり、これより$E[|| \vec e ||^2]$は、
$$\begin{aligned} E[|| \vec e ||^2] &= E[\underbrace{\vec \varepsilon^{\top} (I_n-P_X) \vec \varepsilon}_{\bullet} ] \\[10px] &= E[\tr \{ \vec \varepsilon^{\top} (I_n-P_X) \vec \varepsilon \}] \\ &{\scriptsize (\bulletは二次形式より定数なので\trをつけてもイコール)} \\[10px] &= E[\tr \{ (I_n-P_X) \vec \varepsilon \vec \varepsilon^{\top} \}] \\ &{\scriptsize (\tr(ABC) = \tr(BCA))} \\[10px] &= \tr[ E[ (I_n-P_X) \vec \varepsilon \vec \varepsilon^{\top} ] ] \\ &{\scriptsize (\trとEの交換は可能)} \\[10px] &= \tr[ (I_n-P_X) E[\vec \varepsilon \vec \varepsilon^{\top}] ] \\[10px] &= \tr[ (I_n-P_X) \sigma^2 I_n ] \\[10px] &= \sigma^2 \tr[I_n-P_X] \\[10px] &= \sigma^2 (\tr I_n-\tr P_X) \\[10px] &= \sigma^2 (n-\tr P_X) \end{aligned}$$となります。


ここで$\tr P_X$は、
$$\begin{aligned} \tr P_X &= \tr \{ \vec X (\vec X^{\top} \vec X)^{-1} \vec X^{\top} \} \\[10px] &= \tr \{ (\vec X^{\top} \vec X)^{-1} \vec X^{\top} \vec X \} \\ &{\scriptsize (\tr(ABC) = \tr(BCA))} \\[10px] &= \tr I_d \\[10px] &= d \end{aligned}$$となるため、上記と合わせて、
$$\begin{aligned} E[|| \vec e ||^2] = (n-d) \sigma^2 \end{aligned}$$となります。


以上より$\sigma^2$の不偏推定量$\hat{\sigma}^2$は、
$$\begin{aligned} \hat{\sigma}^2 = \frac{1}{n-d} || \vec e ||^2 ~~~~~ \mathrm{(K)} \end{aligned}$$となります。

すたどく

ちなみに、最尤法で$\vec \beta, \sigma^2$の推定をする（最尤推定量を求める）ことも可能です。この場合は、$\mathrm{(J)}$を$\vec \beta, \sigma^2$でそれぞれ偏微分した式$=0$を解くことになります。
$\sigma^2$に対してのみ最尤法を用いる、ということはないので注意してください。

（補足）

• *¹：実は、最小$2$乗推定量は不偏推定量なのです。
  これは以下の通りに示されます。
  $$\begin{aligned} E[\hat{\vec \beta}] &= E[(\vec X^{\top} \vec X)^{-1} \vec X^{\top} \vec y] \\ &{\scriptsize(\mathrm{(I)}より)} \\[10px] &= E[(\vec X^{\top} \vec X)^{-1} \vec X^{\top} (\vec X \vec \beta + \vec \varepsilon)] \\ &{\scriptsize(\mathrm{(C)}より)} \\[10px] &= E[\vec \beta + (\vec X^{\top} \vec X)^{-1} \vec X^{\top} \vec \varepsilon] \\[10px] &= \vec \beta \\[10px] &{\scriptsize(\mathrm{(D)}より)} \end{aligned}$$
  
  
  
  
• *²：線形推定量とは、被説明変数$\vec y$の線形関数で表される推定量です。
  即ち、$\vec C \vec y$ $(\vec C:$定数ベクトル$)$、の形式で表される推定量です。
  最小$2$乗推定量$\hat{\vec \beta}$は、
  $$\begin{aligned} \hat{\vec \beta} = (\underbrace{(\vec X^{\top} \vec X)^{-1} \vec X^{\top}}_{\vec Cとみる}) \vec y \end{aligned}$$の形式で表されるので線形推定量です。
  
  
  
  
• *^３：ガウス・マルコフの定理をわかりやすく示すと、
  『最小$2$乗推定量$\hat{\vec \beta}$は、それが属するFig3斜線部のうち、分散が最小である』となります。
  
  
  Fig3.

すたどく

ちなみに、不偏な線形推定量のうち（Fig3の斜線部）分散が最小である推定量を”BLUE(Best Linear Unbiased Estimator)”と言います。

学習者

“BLUE”というワードを使うなれば、ガウス・マルコフの定理は『最小$2$乗推定量はBLUE』と主張しているのですね！

すたどく

一点注意があります。
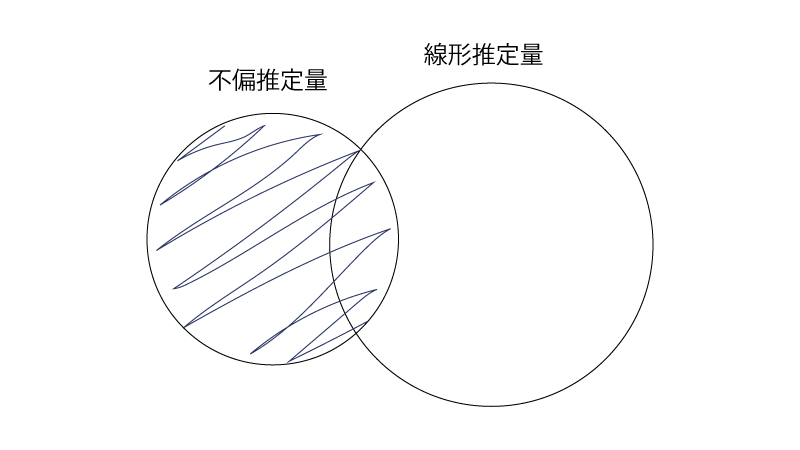
UMVUとは不偏推定量のうち分散が最小である推定量でした。（参照：＜不偏推定量＞）
即ちUMVUは、Fig4の斜線部のうち、分散が最小でした。


よって、ガウス・マルコフの定理は『最小$2$乗推定量はUMVU』と主張しているのではないことに注意してください。

Fig4.

学習者

UMVUにBLUEに横文字が続くと混乱しますね。。

すたどく

うまくFigを使って整理してください。
ついでにもう1つ情報を追加すると、
誤差項に正規性の仮定を置く場合には、最小$2$乗推定量はクラメル・ラオの下限を達成するため（例題2）、UMVUとなります。

学習者

もう勘弁。。。

例題1.
目的変数$y_i$、説明変数$x_{i,1}, x_{i,2} ~~ (i=1, \cdots, n)$に対して、
$$\begin{aligned} \begin{cases} y_i &= \beta_1 x_{i,1} + \beta_2 x_{i,2} + \varepsilon_i \\ \varepsilon_i &\overset{i.i.d}\sim \N(0, \sigma^2) \end{cases} \end{aligned}$$という重回帰モデルを考える。


この時、最小$2$乗推定量$\hat{\beta_1}, \hat{\beta_2}$を求めよ。

解答.

$$\begin{aligned} \vec y &= (y_1, \cdots, y_n)^{\top} \\ \vec \beta &= (\beta_1, \beta_2)^{\top} \\ \vec \varepsilon &= (\varepsilon_1, \cdots, \varepsilon_n)^{\top} \\ \vec X &= \begin{pmatrix} x_{1,1} &x_{1,2} \\ \vdots &\vdots \\ x_{n,1} &x_{n,2} \end{pmatrix} \end{aligned}$$と置くと、題意の重回帰モデルは、
$$\begin{aligned} \vec y = \vec X \vec \beta + \vec \varepsilon \end{aligned}$$と書ける。




正規方程式より、
$$\begin{alignat}{2} \notag &&\vec X^{\top} \vec X \vec \beta &= \vec X^{\top} \vec y \\[20px] \notag &\Rightarrow& \begin{pmatrix} x_{1,1} &\cdots &x_{n,1} \\ x_{1,2} &\cdots &x_{n,2} \end{pmatrix} \begin{pmatrix} x_{1,1} &x_{1,2} \\ \vdots &\vdots \\ x_{n,1} &x_{n,2} \end{pmatrix} \begin{pmatrix} \beta_1 \\ \beta_2 \end{pmatrix} &= \begin{pmatrix} x_{1,1} &\cdots &x_{n,1} \\ x_{1,2} &\cdots &x_{n,2} \end{pmatrix} \begin{pmatrix} y_1 \\ \vdots \\ y_n \end{pmatrix} \\[20px] \notag &\Rightarrow& \begin{pmatrix} \sum_{i=1}^{n} x_{i,1}^2 &\sum_{i=1}^n x_{i,1} x_{i,2} \\ \sum_{i=1}^{n} x_{i,1} x_{i,2} &\sum_{i=1}^{n} x_{i,n}^2 \end{pmatrix} \begin{pmatrix} \beta_1 \\ \beta_2 \end{pmatrix} &= \begin{pmatrix} \sum_{i=1}^n x_{i,1} y_i \\ \sum_{i=1}^n x_{i,2} y_i \end{pmatrix} \\[20px] \notag &\Rightarrow& \begin{pmatrix} \beta_1 \\ \beta_2 \end{pmatrix} &= \begin{pmatrix} \sum_{i=1}^{n} x_{i,1}^2 &\sum_{i=1}^n x_{i,1} x_{i,2} \\ \sum_{i=1}^{n} x_{i,1} x_{i,2} &\sum_{i=1}^{n} x_{i,n}^2 \end{pmatrix}^{-1} \begin{pmatrix} \sum_{i=1}^n x_{i,1} y_i \\ \sum_{i=1}^n x_{i,2} y_i \end{pmatrix} \\ \end{alignat}$$ （$\mathrm{(I)}$にある通り、$\hat{\vec \beta} = (\vec X^{\top} \vec X)^{-1} \vec X^{\top} \vec y$、にいきなり代入しても構いませんが、計算過程のイメージがしやすいように正規方程式から書いてみました）

（補足）

例題1では切片項を含まない重回帰モデルを扱いましたが、切片項を含む重回帰モデルについても流れは同じです。


例えば以下の様に切片項$\beta_0$を追加した重回帰モデルにおける最小$2$乗推定量$\hat{\beta_0},\hat{\beta_1},\hat{\beta_2}$を求めてみましょう。
$$\begin{aligned} \begin{cases} y_i &= \beta_0 + \beta_1 x_{i,1} + \beta_2 x_{i,2} + \varepsilon_i \\ \varepsilon_i &\overset{i.i.d} \sim \N(0, \sigma^2) \end{cases} \end{aligned}$$


この時、
$$\begin{aligned} \vec y &= (y_1, \cdots, y_n)^{\top} \\ \vec \beta &= (\beta_0, \beta_1, \beta_2)^{\top} \\ \vec \varepsilon &= (\varepsilon_1, \cdots, \varepsilon_n)^{\top} \\ \vec X &= \begin{pmatrix} \color{red}{1} &x_{1,1} &x_{1,2} \\ \color{red}{\vdots} &\vdots &\vdots \\ \color{red}{1} &x_{n,1} &x_{n,2} \end{pmatrix} \end{aligned}$$と置くと、題意の重回帰モデルは、
$$\begin{aligned} \vec y = \vec X \vec \beta + \vec \varepsilon \end{aligned}$$と書ける。




正規方程式から、
$$\begin{alignat}{2} \notag &&\vec X^{\top} \vec X \vec \beta &= \vec X^{\top} \vec y \\ \notag &\Rightarrow& \hat{\vec \beta} &= (\vec X^{\top} \vec X)^{-1} \vec X^{\top} \vec y \\ \notag &&&={\small(以下計算略)} \end{alignat}$$

すたどく

正規方程式は$|| \vec y-\vec X \vec \beta||^2$を$\vec \beta$で偏微分した式$=0$とすることで出てきたので、$\vec y = \vec X \vec \beta + \vec \varepsilon$という形でモデルを設定さえすれば正規方程式は成立するのです！

例題2.
目的変数$y_i$、説明変数$x_{i,1}, \cdots, x_{i,d} ~~ (i=1, \cdots, n)$に対して、
$$\begin{aligned} &\begin{cases} y_i &= \beta_1 x_{i,1} + \cdots + \beta_d x_{i,d} + \varepsilon_i \\ \varepsilon_i &\overset{i.i.d}\sim \N(0, \sigma^2) \end{cases} \\ \iff &\begin{cases} \vec y &= \vec X \vec \beta + \vec \varepsilon \\ \vec \varepsilon &\sim \N(\vec 0, \sigma^2 I_n) \end{cases} \end{aligned}$$という重回帰モデルを考える。


この時、最小$2$乗推定量$\hat{\vec \beta}$（これは$\vec \beta$の不偏推定量でした）はクラメル・ラオの下限を達成することを示せ。


ただし、
$$\begin{aligned} \vec X &= \begin{pmatrix} x_{1,1} &\cdots &x_{1,d} \\ \vdots &\ddots &\vdots \\ x_{n,1} &\cdots &x_{n,d} \end{pmatrix} ~~ (\in \mathbb{R}^{n \times d}) \\ \vec y &= (y_1, \cdots, y_n)^{\top} ~~ (\in \mathbb{R}^{n}) \\ \vec \beta &= (\beta_1, \cdots, \beta_d)^{\top} ~~ (\in \mathbb{R}^{d}) \\ \vec \varepsilon &= (\varepsilon_1, \cdots, \varepsilon_n)^{\top} ~~ (\in \mathbb{R}^{n}) \end{aligned}$$とした。

解答.

まずフィッシャー情報行列$I(\vec \beta, \sigma^2)$を求める。


尤度関数$L(\vec \beta, \sigma^2)$は、
$$\begin{aligned} L(\vec \beta, \sigma^2) = \frac{1}{(2 \pi \sigma^2)^{\frac{n}{2}}} \exp \{ -\frac{1}{2 \sigma^2} || \vec y-\vec X \vec \beta||^2 \} \end{aligned}$$であるから、
対数尤度関数$l(\vec \beta, \sigma^2)$は、
$$\begin{aligned} l(\vec \beta, \sigma^2) &= -\frac{n}{2} \log (2 \pi \sigma^2)-\frac{1}{2 \sigma^2} || \vec y-\vec X \vec \beta||^2 \\[10px] &= -\frac{n}{2} \log (2 \pi \sigma^2)-\frac{1}{2 \sigma^2} (\vec y^{\top} \vec y-2\vec \beta^{\top} \vec X^{\top} \vec y + \vec \beta^{\top} \vec X^{\top} \vec X \vec \beta) \\ &{\scriptsize((G)参照)} \end{aligned}$$となる。




$l(\vec \beta, \sigma^2)$を各要素で偏微分すると、
$$\begin{aligned} \frac{\partial l(\vec \beta, \sigma^2)}{\partial \vec \beta} &= -\frac{1}{2 \sigma^2} (-2 \vec X^{\top} \vec y + 2 \vec X^{\top} \vec X \vec \beta) \\[10px] &= \frac{1}{\sigma^2} (\vec X^{\top} \vec y-\vec X^{\top} \vec X \vec \beta) \\[20px] \frac{\partial l(\vec \beta, \sigma^2)}{\partial (\sigma^2)} &= -\frac{n}{2} \cdot \frac{2 \pi}{2 \pi \sigma^2} + \frac{1}{2 \sigma^4} ||\vec y-\vec X \vec \beta||^2 \\[10px] &= -\frac{n}{2 \sigma^2} + \frac{1}{2 \sigma^4} ||\vec y-\vec X \vec \beta||^2 \\[20px] \frac{\partial^2 l(\vec \beta, \sigma^2)}{\partial \vec \beta \partial \vec \beta^{\top}} &= \frac{1}{\sigma^2} (-\vec X^{\top} \vec X) \\[10px] &= -\frac{1}{\sigma^2} \vec X^{\top} \vec X \\[20px] \frac{\partial^2 l(\vec \beta, \sigma^2)}{\partial (\sigma^2)^2} &= \frac{n}{2\sigma^4}-\frac{1}{\sigma^6} ||\vec y-\vec X \vec \beta||^2 \\[20px] \frac{\partial^2 l(\vec \beta, \sigma^2)}{\partial \vec \beta \partial \sigma^2} &= -\frac{1}{\sigma^4} (\vec X^{\top} \vec y-\vec X^{\top} \vec X \vec \beta) \end{aligned}$$となる。




これらより、
$$\begin{aligned} E[\frac{\partial^2 l(\vec \beta, \sigma^2)}{\partial \vec \beta \partial \vec \beta^{\top}}] &= E[-\frac{1}{\sigma^2} \vec X^{\top} \vec X] \\[10px] &= -\frac{1}{\sigma^2} \vec X^{\top} \vec X \\[20px] E[\frac{\partial^2 l(\vec \beta, \sigma^2)}{\partial (\sigma^2)^2}] &= E[\frac{n}{2 \sigma^4}-\frac{1}{\sigma^6} ||\vec y-\vec X \vec \beta||^2] \\[10px] &= \frac{n}{2 \sigma^4}-\frac{1}{\sigma^6} E[||\vec y-\vec X \vec \beta||^2] \\[10px] &= \frac{n}{2 \sigma^4}-\frac{1}{\sigma^6} E[||\vec \varepsilon||^2] \\[10px] &= \frac{n}{2 \sigma^4}-\frac{1}{\sigma^6}(n \sigma^2) \\[10px] &= -\frac{n}{2 \sigma^4} \\[20px] E[\frac{\partial^2 l(\vec \beta, \sigma^2)}{\partial \vec \beta \partial \sigma^2}] &= E[-\frac{1}{\sigma^4} (\vec X^{\top} \vec y-\vec X^{\top} \vec X \vec \beta)] \\[10px] &= -\frac{1}{\sigma^4} \vec X^{\top} E[(\vec y-\vec X \vec \beta)] \\[10px] &= -\frac{1}{\sigma^4} \vec X^{\top} E[\vec \varepsilon] \\[10px] &= \vec 0 \\ &{\scriptsize(E[\vec \varepsilon]= \vec 0より)} \end{aligned}$$となる。




以上よりフィッシャー情報行列$I(\vec \beta, \sigma^2)$は、
$$\begin{aligned} I(\vec \beta, \sigma^2) (&= \begin{pmatrix} -E[\frac{\partial^2 l(\vec \beta, \sigma^2)}{\partial \vec \beta \partial \vec \beta^{\top}} &-E[\frac{\partial^2 l(\vec \beta, \sigma^2)}{\partial \vec \beta \partial \sigma^2}]] \\ -E[\frac{\partial^2 l(\vec \beta, \sigma^2)}{\partial \vec \beta \partial \sigma^2}]] &-E[\frac{\partial^2 l(\vec \beta, \sigma^2)}{\partial (\sigma^2)^2}] \end{pmatrix} ) \\[20px] &= \begin{pmatrix} \frac{1}{\sigma^2} \vec X^{\top} \vec X &\vec 0 \\ \vec 0 &\frac{n}{2 \sigma^4} \end{pmatrix} \end{aligned}$$となり、
クラメル・ラオの不等式は、
$$\begin{aligned} \begin{pmatrix} V[\hat{\vec \beta}] &\vec 0 \\ \vec 0 &V[\hat{\sigma}^2] \end{pmatrix} &\succeq I(\vec \beta, \sigma^2)^{-1} \\[20px] &= \begin{pmatrix} \sigma^2 (\vec X^{\top} \vec X)^{-1} &\vec 0 \\ \vec 0 &\frac{2 \sigma^4}{n} \end{pmatrix} \\[20px] \Rightarrow &\begin{cases} V[\hat{\vec \beta}] &\geqq \sigma^2 (\vec X^{\top} \vec X)^{-1} \\ V[\hat{\sigma}^2] &\geqq \frac{2 \sigma^4}{n} \end{cases} \end{aligned}$$となる。




ところで、
$$\begin{aligned} V[\hat{\vec \beta}] = \sigma^2 (\vec X^{\top} \vec X)^{-1} \end{aligned}$$であったため（『2. 推定量の性質』＞①）、最小$2$乗推定量$\hat{\vec \beta}$はクラメル・ラオの下限を達成している。

（補足）

不偏推定量$\hat{\sigma}^2$（$\mathrm{(K)}$）についても、クラメル・ラオの下限を達成するかを確認してみましょう。




『2. 推定量の性質』＞②の、
$$\begin{aligned} \frac{(n-d) \hat{\sigma}^2}{\sigma^2} \sim \chi^2(n-d) \end{aligned}$$より、
$$\begin{aligned} V[\frac{(n-d) \hat{\sigma}^2}{\sigma^2}] &= 2(n-d) \\ &{\scriptsize(Y \sim \chi^2(m)であればV[Y]=2m)} \end{aligned}$$となります。




これより、
$$\begin{aligned} V[\hat{\sigma}^2] &= \frac{(\sigma^2)^2}{(n-d)^2} \cdot 2 (n-d) \\[10px] &= \frac{2 \sigma^4}{n-d} \gt \frac{2 \sigma^4}{n} ~~ {\small(クラメル・ラオの下限)} \end{aligned}$$となり、不偏推定量$\hat{\sigma}^2$はクラメル・ラオの下限を達成しません。




しかし、実は不偏推定量$\hat{\sigma}^2$はUMVUとなっています。
なぜなら、不偏推定量$\hat{\sigma}^2$は完備十分統計量の関数となっているためです。

学習者

ある不偏推定量がUMVUであることを示す方法は、
①その推定量がクラメル・ラオの不等式の下限を達成することを示す
②その推定量が完備十分統計量（またはその関数）であることを示す
でしたね。
（参照：＜不偏推定量＞：「4. ある不偏推定量がUMVUであることの示し方」）
今回は①では示されませんでしたが、②で示されるということですね。

すたどく

その通りです。具体的には以下の通りとなります。

（不偏推定量$\hat{\sigma}^2$は完備十分統計量の関数であることの確認）

$\vec y$の確率密度関数$f(\vec y; \vec \beta, \sigma^2)$は、
$$\begin{aligned} f(\vec y; \vec \beta, \sigma^2) (&= L(\vec \beta, \sigma^2)) \\[10px] &= \frac{1}{(2 \pi \sigma^2)^{\frac{n}{2}}} \exp \{ -\frac{1}{2 \sigma^2} || \vec y-\vec X \vec \beta||^2 \} \\[10px] &= \frac{1}{(2 \pi)^{\frac{n}{2}}} \exp \{ -\frac{n}{2} \log (\sigma^2)-\frac{1}{2 \sigma^2} (\vec y^{\top} \vec y-2\vec \beta^{\top} \vec X^{\top} \vec y + \vec \beta^{\top} \vec X^{\top} \vec X \vec \beta) \} \\[10px] &= \underbrace{\frac{1}{(2 \pi)^{\frac{n}{2}}}}_{h(\vec y)} \exp \{ \underbrace{-\frac{1}{2 \sigma^2}}_{\phi_1(\vec \beta, \sigma^2)} \underbrace{\vec y^{\top} \vec y}_{T_1(\vec y)} + \underbrace{\frac{1}{\sigma^2} \vec \beta^{\top}}_{\phi_2(\vec \beta, \sigma^2)} \underbrace{\vec X^{\top} \vec y}_{T_2(\vec y)}-\{ \underbrace{\frac{n}{2} \log(\sigma^2)-\vec \beta^{\top} \vec X^{\top} \vec X \vec \beta}_{c(\vec \beta, \sigma^2)} \} \} \end{aligned}$$と変形されるため（最後の形は、＜完備十分統計量＞：「2. 指数型分布族と完備十分統計量」に形を揃えた）、$(\vec y^{\top} \vec y, \vec X^{\top} \vec y)$は$(\vec \beta, \sigma^2)$の完備十分統計量となります。




また$\hat{\sigma}^2$について、
$$\begin{aligned} \hat{\sigma}^2 &= \frac{1}{n-d} || \vec e||^2 \\[10px] &= \frac{1}{n-d} \vec e^{\top} \vec e \\[10px] &= \frac{1}{n-d} (\vec y-\hat{\vec y})^{\top} (\vec y-\hat{\vec y}) \\[10px] &= \frac{1}{n-d} (\vec y^{\top} \vec y-\vec y^{\top} \hat{\vec y}-\hat{\vec y}^{\top} \vec y + \hat{\vec y}^{\top} \hat{\vec y}) \\[10px] &= \frac{1}{n-d} (\vec y^{\top} \vec y-\vec y^{\top} \hat{\vec y}) \\ &{\scriptsize(Fig1の位置関係より\vec y^{\top} \hat{\vec y}=\hat{\vec y}^{\top} \vec y=\hat{\vec y}^{\top} \hat{\vec y}))} \\[10px] &= \frac{1}{n-d} (\vec y^{\top} \vec y-\vec y^{\top} \vec X \hat{\vec \beta}) \\[10px] &= \frac{1}{n-d} (\vec y^{\top} \vec y-(\hat{\vec \beta}^{\top} \vec X^{\top} \vec y)^{\top}) \end{aligned}$$と$(\vec y^{\top} \vec y, \vec X^{\top} \vec y)$の関数であるため、$\hat{\sigma}^2$は完備十分統計量の関数であることが示されました。

まとめ.

• 最小$2$乗推定量とは残差ベクトルの$2$乗を最小化する推定量であり、正規方程式から求められる。
  
  
  
• 最小$2$乗推定量はBLUEであり、誤差項に正規性の仮定がおける場合にはUMVUでもある。