$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}}$
ここでは十分統計量の特殊例である「完備十分統計量」を扱います。
やや抽象度の高い内容なので、一度にすべてを理解できなくても構いません。
はい、最初は雰囲気をつかむにとどめておきます。
さて、「完備十分統計量」とはざっくり言うとどの様なものでしょうか?
「完備十分統計量」とは十分統計量のうち最も情報を圧縮したものです。
定義からして直感的にはわかりにくいですが、例とともにイメージをつくりあげてください。
1. 完備十分統計量の定義
(定義)
$$\begin{aligned} 『十分統計量T(\vec X)が分布パラメータ\theta&の完備(完備十分統計量)』 \\ &\Updownarrow \\ 『\textcolor{red}{任意の関数g}に対して、E[g(T(\vec X))] ~ (&= \int g(T(\vec x)) \cdot f(\vec x; \theta) d \vec x) = 0 ~~ (\textcolor{red}{\forall \theta}) \\[15px] \Rightarrow g \equiv 0 ~~ &(\textcolor{red}{\forall \theta})』 \end{aligned}$$となります。
初見だとイマイチわからないと思いますので、例を確認してみましょう。
例題1.
$X \sim \Bin(n, p) ~~ \small{(n \in \mathbb{N}, 0 \lt p \lt 1)}$である時、統計量$T(X)=X$は$p$の完備十分統計量であることを示せ。
解答.
$E[g(T(X))] = 0 ~~ (\forall p)$を考えると、
$$\begin{alignat}{2} && E[g(T(X))] &= 0 ~~ (\forall p) \notag \\[10px] &\Rightarrow& E[g(X)] &= 0 ~~ (\forall p) \notag \\ &&&{\scriptsize (T(X)=Xより)} \notag \\[10px] &\Rightarrow& \sum_{x=0}^{n} \{ g(x) \cdot \binom{n}{x} p^x (1-p)^{n-x} \} &= 0 ~~ (\forall p) \notag \\[10px] &\Rightarrow& \sum_{x=0}^{n} \{ g(x) \cdot \binom{n}{x} (\frac{p}{1-p})^x \} &= 0 ~~ (\forall p) \notag \\ &&&{\scriptsize (両辺を(1-p)^nで割って整理した)} \notag \end{alignat}$$となる。
上式の左辺は$(\frac{p}{1-p})$の$n$次式となっており、$(\frac{p}{1-p})$は$(0, \infty)$の任意の値を取るので、上式が成立するためには、
$$\begin{alignat}{2} &&g(x) \cdot \binom{n}{x} &= 0 ~~ (x=0, \ldots, n; \forall p) \notag \\[10px] &\Rightarrow& g(x) &= 0 ~~ (x=0, \ldots, n; \forall p) \notag \end{alignat}$$が成立する必要がある。
よって$g(t(x))=0 ~~ (x=0, \ldots, n; \forall p)$が示されたため、$T(X)=X$は$p$の完備十分統計量である。
例題2.
$X_i \overset{i.i.d}\sim \Po(\lambda) ~~ \small{(i=1, \ldots, n; \lambda \gt 0)}$である時、$T(\vec X) = \sum_{i=1}^{n} X_i$は$\lambda$の完備十分統計量であることを示せ。
解答.
$X_1, \ldots, X_n$は互いに独立に$\Po(\lambda)$に従うことから、
$$\begin{aligned} T(\vec X)(=\sum_{i=1}^{n} X_i) \sim \Po(n \lambda) \end{aligned}$$となる。(参照:<分布関数と母関数>:例題1)
$E[g(T(\vec X))] = 0 ~~ (\forall \lambda)$を考えると、
$$\begin{alignat}{2} && E[g(T(\vec X))] &= 0 ~~ (\forall \lambda) \notag \\[10px] &\Rightarrow& \sum_{t=0}^{\infty} g(t) \cdot \frac{(n \lambda)^{t} e^{-(n \lambda)}}{t!} &= 0 ~~ (\forall \lambda) \notag \\ &&&{\scriptsize (\Po(n \lambda)に対応する確率関数は\frac{(n \lambda)^{t} e^{-(n \lambda)}}{t!})} \notag \\[10px] &\Rightarrow& \sum_{t=0}^{\infty} g(t) \cdot \frac{ (n \lambda)^t }{t!} &= 0 ~~ (\forall \lambda) \notag \\ &&&{\scriptsize (両辺をe^{-(n \lambda)}(\gt 0)で除した)} \notag\end{alignat}$$となる。
上式が成立するためには、
$$\begin{aligned} g(t) = 0 ~~ (t=0,1,\ldots) \end{aligned}$$が成立する必要がある。
よって$g(t(\vec x))=0 ~~ (x=0, \ldots, n; \forall \lambda)$が示されたため、$T(\vec X) = \sum_{i=1}^{n} X_i$は$\lambda$の完備十分統計量である。
- 逆に、完備十分統計量ではない例を確認してみましょう。
$$\begin{aligned} X_i \overset{i.i.d}\sim \Po(\lambda) ~~ \small{(i=1, \ldots, n)} \\ T(\vec X) = (X_1, \sum_{i=1}^{n} X_i) \end{aligned}$$である時、関数$g$として
$$\begin{aligned} g(t_1, t_2) = t_1-\frac{1}{n} t_2 ~~ \small{(t_1, t_2 \in \mathbb{N})} \end{aligned}$$を考えます。
この時、
$$\begin{aligned} E[g(T(\vec X))] &= E[X_1]-E[\frac{1}{n} \sum_{i=1}^{n} X_i] \\ &= \lambda-\lambda \\ &= 0 \end{aligned}$$が成立しますが、明らかに$g \equiv 0$ではないため、$T(\vec X) = (X_1, \sum_{i=1}^{n} X_i)$は完備十分統計量ではありません。
この$T(\vec X)$では$\lambda$についての情報を圧縮しきれていないということですね!
2. 指数型分布族と完備十分統計量
(定理)
ある分布が指数型分布族に属する時、即ち、この分布に従う確率変数$X$の確率密度関数(または確率関数)$f(x)$が($\theta$を分布パラメータとして)、
$$\begin{aligned} f(x) = h(x) \cdot \exp[ \sum_{i=1}^{s} T_i(x) \phi_i(\theta)-c(\theta) ] \end{aligned}$$の形式で書ける時、(ある条件下で*)$T=(T_1, \ldots, T_s)$は$\theta$の完備十分統計量となります。
*:その条件とは以下ですが、統計検定1級の範囲内ではこの条件はほぼ満たされてると思われます。
・$T=(T_1, \ldots, T_s)$の分散共分散行列が正則(逆行列をもつ)
かつ
・$\phi_1, \ldots, \phi_s$が線形独立(ある区間内を独立に動く)
例1.
$X \sim \Po(\lambda)$である時、その確率関数$p(x)$は、
$$\begin{aligned} p(x) = \underbrace{\frac{1}{x!}}_{h(x)} \cdot \exp [ \underbrace{x}_{T(x)} \underbrace{\log \lambda}_{\phi(\lambda)}-\underbrace{\lambda}_{c(\lambda)} ] \end{aligned}$$と書くことができるので、$T(X)=X$は$\lambda$の完備十分統計量となる。
3. おまけ
- 完備十分統計量は情報が最も圧縮された十分統計量でしたが、イメージとしては以下Fig1の通りになります。
Fig1.
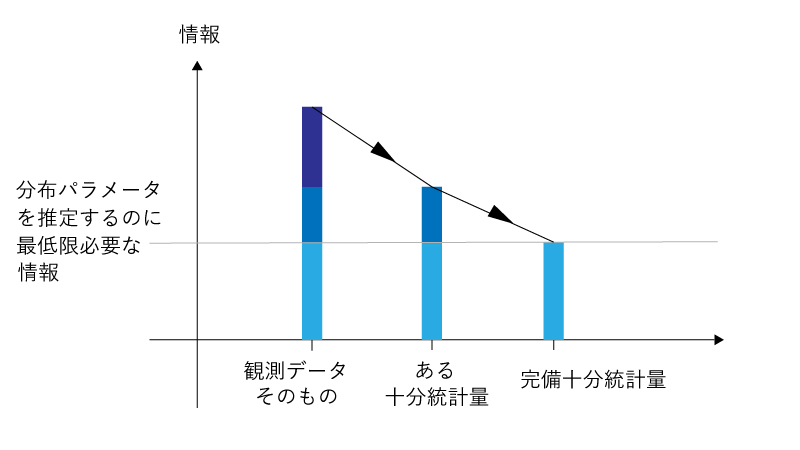
- 完備十分統計量の使い道をまだ紹介していませんが、完備十分統計量は<不偏推定量>において重要な役割を果たします。
まとめ.
- 「完備十分統計量」とは、十分統計量のうち情報を最も圧縮したものである。
- 指数型分布族においては必ず完備十分統計量は存在し、その導出は指数型分布族の定義式に変形することで行える。




