$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}}$
「推測」とは、興味のある未知の母集団について、観測データからその特徴を推し測ることです。その中に$2$種類:「推定」「検定」があります。
今回扱うのは「推定」ですね。
はい。「推定」とは未知の分布パラメータを当てにいくことです。
その道具となる「推定量」は観測データから構成する必要があるため、統計量になっています。
統計量は観測データから構成される量でしたもんね。
ここでは「推定量」がもっていると望ましい性質を扱っていきます。
0. 推定量とは?
推定量とは、分布パラメータを当てにいくための統計量、です。
以下では分布パラメータ$\theta$に対して”$\hat{\theta}$”の様に”$~\hat{}~$”をつけたものは推定量であることを表します。
また”$\hat{\theta}_{n}$”の様に右下添字”$_{n}$”をつける場合には、$n$個のサンプルデータから構成された推定量を表します。
ここからは推定量がもっていると望ましい性質$4$つを紹介します。
ただし必ずしも$4$つの性質すべてを満たすべきというものではありません。
1. 不偏性
(定義)
(真の分布パラメータを$\theta$として)
『ある推定量$\hat{\theta}_{n}$が不偏性をもつ(不偏推定量である)』とは、 $$\begin{aligned} E[\hat{\theta}_{n}] = \theta \end{aligned}$$が成立することです。
(説明)
これは、
『推定量$\hat{\theta}_{n}$は真の分布の下で一定のバラつきをもって算出されますが、そのバラつきについて期待値をとると、真のパラメータ$\theta$に一致する』ということです。
不偏性をもつ推定量$\hat{\theta}_{n}$のイメージFigは以下の様になります。
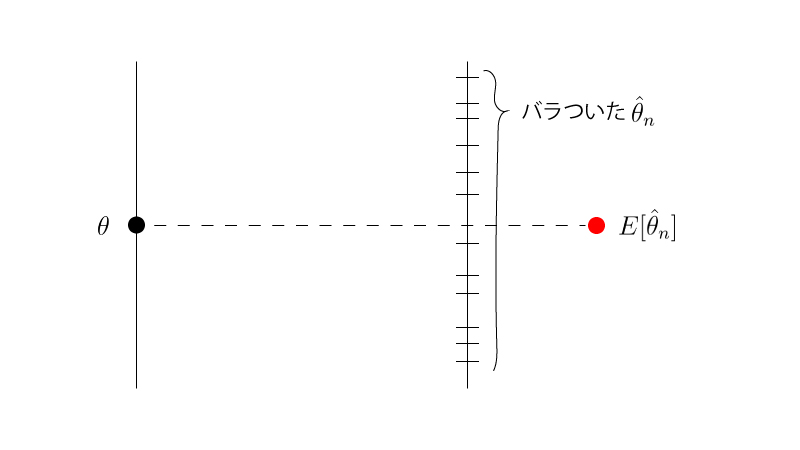
逆に不偏性をもたない推定量$\tilde{\theta}_{n}$(注意:”$~\tilde{}~$”は「チルダ」とよみます。”$~\hat{}~$”と区別してください。)のイメージFigは以下の様になります。
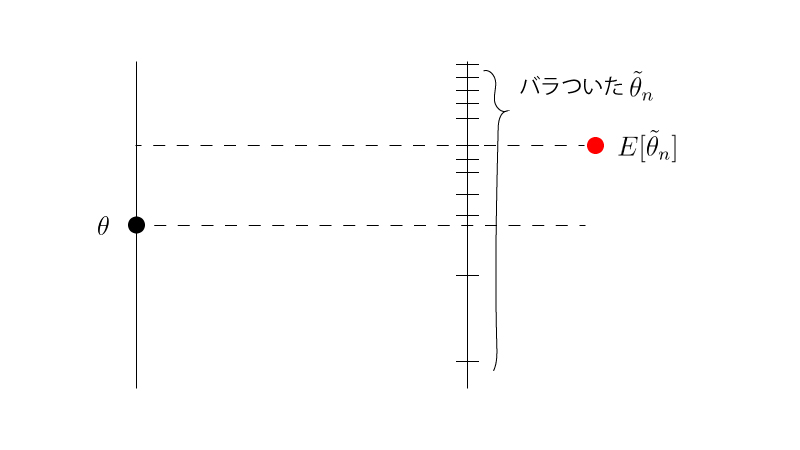
推定量の性質を覚える際には、この様なイメージFigを頭に浮かべておくとよいと思います。
例題1.
$X_i \overset{i.i.d}\sim \N(\mu, \sigma^2) ~~ {\small (i=1, \ldots, n)}$である時、標本分散$V_1^2$、不偏分散$V_2^2$は不偏性をもつか確認せよ。
ただし、
$$\begin{aligned} V_1^2 &= \frac{1}{n} \sum_{i=1}^n (X_i-\bar{X_n})^2 \\ V_2^2 &= \frac{1}{n-1} \sum_{i=1}^n (X_i-\bar{X_n})^2 \end{aligned}$$である。
解答.
一般に成立する
$$\begin{aligned} \sum_{i=1}^n (X_i-\bar{X}_n)^2 = \sum_{i=1}^n (X_i-\mu)^2-n(\bar{X}_n-\mu)^2 \end{aligned}$$の両辺について期待値をとると、
$$\begin{aligned} E[\sum_{i=1}^n (X_i-\bar{X}_n)^2] &= E[\sum_{i=1}^n (X_i-\mu)^2-n(\bar{X}_n-\mu)^2] \\[10px] &= E[\sum_{i=1}^n (X_i-\mu)^2]-n \cdot E[(\bar{X}_n-\mu)^2] \\[10px] &= \sum_{i=1}^n E[(X_i-\mu)^2]-n \cdot \frac{\sigma^2}{n} \\ &{\scriptsize (\bar{X}_n \sim \N(\mu, \frac{\sigma^2}{n})から(V[\bar{X}_n]=)E[(\bar{X}_n-\mu)^2] = \frac{\sigma^2}{n})} \\[10px] &= n \sigma^2-\sigma^2 \\ &{\scriptsize ((V[\bar{X}_n]=)E[(X_i-\mu)^2]=\sigma^2)} \\[10px] &= (n-1) \sigma^2 \end{aligned}$$となる。
よって、
$$\begin{aligned} E[\frac{1}{n-1} \sum_{i=1}^n (X_i-\bar{X_n})^2] = \sigma^2 \end{aligned}$$となるので、推定量$\hat{\sigma}^2 = \frac{1}{n-1} \sum_{i=1}^n (X_i-\bar{X_n})^2$は不偏性をもつ。
つまり、不偏分散$V_2^2$は不偏性をもち、標本分散$V_1^2$は不偏性をもたない。
お気づきの方もいらっしゃるかと思いますが、不偏分散の「不偏」とは「不偏性」から由来しています。
- 本例題では『$\mu:$ unknownである時に$\sigma^2$を推定したい』という状況を暗に想定しています。
ところで『$\mu:$ known』である時は、
$$\begin{aligned} E[\frac{1}{n} \sum_{i=1}^n (X_i-\mu)^2] =\sigma^2 \end{aligned}$$であるから、推定量$\tilde{\sigma}^2 = \frac{1}{n} \sum_{i=1}^n (X_i-\mu)^2$は不偏性をもちます。
$\mu$がknownなのかunknownなのか、即ち、推定量の中に$\mu$を組み込めるか組み込めないかを意識する必要があるのですね。
ここから先は「2. 一致性」「3. 漸近正規性」「4. 漸近有効性」を扱いますが、これら$3$つの性質は「漸近論(サンプルサイズ$n$が十分大きい時に推定量の妥当性を評価するための理論)」に含まれます。すでに扱った「1. 不偏性」はこの「漸近論」に含まれないため、別個の扱いとしました。
2. 一致性
(定義)
(真の分布パラメータを$\theta$として)
『ある推定量$\hat{\theta}_{n}$が一致性をもつ(一致推定量である)』とは、
$$\begin{aligned} \hat{\theta}_{n} \overset{\displaystyle {p}}\longrightarrow \theta \end{aligned}$$が成立することです。
(説明)
これはざっくり言うなれば、 『$n$が十分大きくなれば、推定量$\hat{\theta}_{n}$は真のパラメータ$\theta$に近づいていく』ということです。
正確に言うなれば、推定量$\hat{\theta}_{n}$が真のパラメータ$\theta$に確率収束するということで、これは『任意の$\varepsilon {\small (\gt 0)}$に対して、推定量$\hat{\theta}_{n}$と真のパラメータ$\theta$との差分が$\varepsilon$より大きくなる確率は、$n$を十分大きくすれば$0$に収束する』ということでした。(参照:<極限定理>)
イメージFigとしては以下の様になります*。
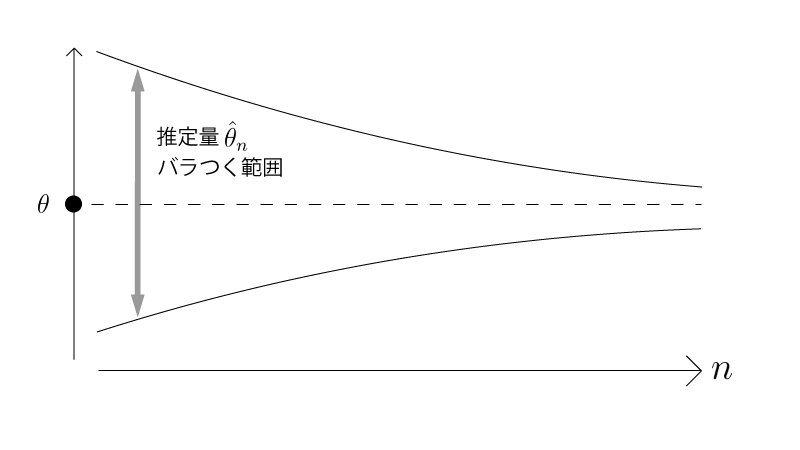
*:イメージFigでは推定量の分散が$0$に収束する様になっていますが、正確には推定量の分散は$0$に収束する必要はありません。こちらはあくまでもイメージです。
(分散が$0$に収束しないが、ある値に確率収束する例)
$$\begin{aligned} X_{n} = \begin{cases} 0 ~~ ({\small with ~ probability} ~ \frac{n-1}{n}) \\ n ~~ ({\small with ~ probability} ~ \frac{1}{n}) \end{cases} \end{aligned}$$
この時、
$$\begin{aligned} V[X_n]=n-1 \\ \Rightarrow \lim_{n \to \infty} V[X_n] = \infty \end{aligned}$$となりますが、$X_n$は$0$に確率収束します。
例題2.
$X_i \overset{i.i.d}\sim \N(\mu, \sigma^2) ~~ {\small (i=1, \ldots, n)}$である時、標本分散$V_1^2$、不偏分散$V_2^2$は一致性をもつか確認せよ。
ただし、
$$\begin{aligned} V_1^2 &= \frac{1}{n} \sum_{i=1}^n (X_i-\bar{X_n})^2 \\ V_2^2 &= \frac{1}{n-1} \sum_{i=1}^n (X_i-\bar{X_n})^2 \end{aligned}$$である。
解答.
一般に成立する
$$\begin{aligned} \sum_{i=1}^n (X_i-\bar{X}_n)^2 = \sum_{i=1}^n (X_i-\mu)^2-n(\bar{X}_n-\mu)^2 \end{aligned}$$の両辺について$n$で割ると、
$$\begin{aligned} \frac{1}{n} \sum_{i=1}^n (X_i-\bar{X}_n)^2 = \underbrace{\frac{1}{n} \sum_{i=1}^n (X_i-\mu)^2}_{(1)}-\underbrace{(\bar{X}_n-\mu)^2}_{(2)} \end{aligned}$$となる。
ここで上式の$\mathrm{(1),(2)}$について、
$$\begin{aligned} \mathrm{(1)} &\overset{\displaystyle {p}}\longrightarrow \sigma^2 \\ \mathrm{(2)} &\overset{\displaystyle {p}}\longrightarrow 0 \end{aligned}$$となる。
($\mathrm{(1)} \overset{\displaystyle {p}}\longrightarrow \sigma^2$、は大数の法則より。(←$Y_i = (X_i-\mu)^2$とおくと$\mathrm{(1)}$は$\bar{Y}_n$に相当し、大数の法則より$\bar{Y}_n\overset{\displaystyle {p}}\longrightarrow E[Y_i]$となる。))
($\mathrm{(2)} \overset{\displaystyle {p}}\longrightarrow 0$、は大数の法則($\bar{X}_n\overset{\displaystyle {p}}\longrightarrow \mu$)と連続写像定理より)
以上とスルツキーの定理$(\mathrm{plim}(X_n + Y_n) = \mathrm{plim}(X_n) + \mathrm{plim}(Y_n))$より、
$$\begin{aligned} \frac{1}{n} \sum_{i=1}^n (X_i-\bar{X}_n)^2 \overset{\displaystyle {p}}\longrightarrow \sigma^2 + 0 = \sigma^2 \end{aligned}$$となり、また、
$$\begin{aligned} \frac{1}{n-1} \sum_{i=1}^n (X_i-\bar{X}_n)^2 = \frac{n}{n-1} \cdot \frac{1}{n} \sum_{i=1}^n (X_i-\bar{X}_n)^2 \overset{\displaystyle {p}}\longrightarrow 1 \cdot \sigma^2 = \sigma^2 \end{aligned}$$となる。
よって、$V_1^2, V_2^2$ともに一致性をもつ。
本例題では$V_1^2, V_2^2$の一致性を確認しましたが、大数の法則から『$\bar{X}_n \overset{\displaystyle {p}}\longrightarrow \mu$』であるため、もちろん$\bar{X}_n$も一致性をもちます。
ここまで「不偏性」と「一致性」を扱ってきましたが、両者を明確に区別してください。「不偏性」は漸近論の枠組みに入らず「一致性」は入るので、「不偏性」では$n$の大小は不問ですが、「一致性」では$n$が十分大きい状況を想定しています。
3. 漸近正規性
(定義)
(真の分布パラメータを$\theta$として)
『ある推定量$\hat{\theta}_{n}$が漸近正規性をもつ』とは、
$$\begin{aligned} {\sqrt n} (\hat{\theta}_{n}-\theta) \overset{\displaystyle {d}}\longrightarrow \N(0, V[\theta]) ~~~~~ \mathrm{(A)} \end{aligned}$$が成立することです。
(説明)
これは『${\sqrt n} (\hat{\theta}_{n}-\theta)$が平均$0$、分散$V[\theta]$の正規分布に分布収束する』ということです。
そして、漸近正規性による嬉しさとは、 ある推定量が漸近正規性をもつ時、その推定量について正規近似ができることになり区間推定・検定の方式として正規分布のそれを用いることができるという点です。
4. 漸近有効性
(定義)
(真の分布パラメータを$\theta$として)
『ある推定量$\hat{\theta}_{n}$が漸近有効性をもつ』とは、
$$\begin{aligned} {\sqrt n} (\hat{\theta}_{n}-\theta) \overset{\displaystyle {d}}\longrightarrow \N(0, \frac{1}{I_1(\theta)}) \end{aligned}$$が成立することです。
(ただし、$I_1(\theta)$はサンプルサイズ$1$の場合のフィッシャー情報量)
(説明)
これは漸近正規性の上で、$V[\theta] = \frac{1}{I_1(\theta)}$、が成立することです。
つまり、漸近有効性は漸近正規性の特殊パターンとなります。
以下重要な事実を紹介します。
①:漸近正規性をもつ推定量は漸近的に不偏推定量とみなせます。
($\mathrm{(A)}$から$n$が十分大きい時に、$E[\hat{\theta}_{n}] \fallingdotseq \theta$、となることより)
②:(実は)不偏推定量の分散の下限はフィッシャー情報量の逆数になっています。
(参照:<不偏推定量>:「クラメル・ラオの式」)
→①②より、漸近有効性をもつ推定量の分散は、漸近正規性をもつ推定量のクラスの中で最小となります。
まとめ.
- 推定量がもっていると望ましい性質として【不偏性・一致性・漸近正規性・漸近有効性】を紹介した。
- 【不偏性】はサンプルサイズ$n$の大小を問わないが、【一致性・漸近正規性・漸近有効性】はサンプルサイズ$n$が十分大きい状況下での性質である。






