『くり返しの公式』とはどういったものでしょうか?
条件つき分布や周辺分布が出てくる時に、期待値や分散を求める公式です。
今回は『期待値のくり返しの公式』を扱い、次回は『分散のくり返しの公式』を扱います。
公式において注意すべき点はありますか?
どの確率分布に対して期待値をとっているのか、を常に意識することが大切です。<期待値のくり返しの公式><分散のくり返しの公式>では$E$や$V$の右上添字はその添字変数についての確率分布を考えるということを意味しています。
たしかに複数の変数が出てくるので、その意識は大切ですね!
1. 『期待値のくり返しの公式』
1-1. 『期待値のくり返しの公式』の説明
($X, Y$は確率変数とします)
期待値のくり返しの公式として、
$$ \begin{aligned} \boldsymbol{E^X[X] = E^Y[ E^{X|Y}[X|Y] ]} ~~~~~ \mathrm{(A)}\end{aligned}$$が成立します。
- $\mathrm{(A)}$の”$E^{X|Y}[X|Y]$”は$Y$の関数となっており、それを$Y$について期待値計算したものが$E^X[X]$になるわけです。 つまり、$\mathrm{(A)}$の右辺は「一度$Y$で条件づけた期待値を、さらに$Y$について期待値をとる」という作業をしています。
- $\mathrm{(A)}$の右辺は$$ \begin{aligned} E^Y[ E^{X|Y}[X|Y] ] = \int_y E^{X|Y}[X|Y=y] \cdot f_Y(y) dy \\ ({\small または} \sum_y E^{X|Y}[X|Y=y] \cdot Pr\{Y=y\}) \end{aligned} $$と書くことができます。
(期待値の定義の復習)
期待値のくり返しの公式はイメージがやや難しいですが、以下の例を通じてイメージを確立してください。
例1.
ある製品は国内の$2$ヶ所の工場A, Bでのみ生産されており、それぞれの製品寿命の平均は$2.5$年、$4$年であると報告されている。また、工場A, Bで生産された商品の流通割合は$4:6$であることがわかっている。
この時、手元に届いた製品の製品寿命の期待値を考える。
確率変数$X, Y$をそれぞれ製品寿命、製品が生産された工場($y=0, 1$が工場A, Bに対応)とすると、$$ \begin{aligned} E^{X|Y}[X|Y=y] &= \begin{cases} 2.5 ~~ (y=0) \\ 4.0 ~~ (y=1) \end{cases} \\ Pr\{ Y=0 \} &= 0.4 \\ Pr\{ Y=1 \} &= 0.6 \end{aligned}$$となる。
この時、$E^X[X]$は $$ \begin{aligned} E^X[X] &= E^Y[E^{X|Y}[E|Y]] \\ &{\scriptsize (期待値のくり返しの公式より)} \\[5px] &= \sum_y \{E^{X|Y}[X|Y=y] \cdot Pr\{ Y=y \}\} \\[5px] &= 2.5 \cdot Pr\{ Y=0 \} + 4.0 \cdot Pr\{ Y=1 \} \\[5px] &= 2.5 \cdot 0.4 + 4.0 \cdot 0.6 \\[5px] &= 3.4 \end{aligned}$$
この例の様に$E^{X|Y}[X|Y]$と$Y$の確率関数(確率密度関数)しか与えられない場合には、期待値のくり返しの公式が役立ちます。
イメージをより確立するためにもう1つ例を確認してみましょう!
例2.
高血圧の患者さんを対象として、薬A vs 薬B、という臨床試験を行ったとする。
この時、確率変数$X, Y$を以下の通りとする。
$$ \begin{aligned} &X: {\small (薬の内服後の)血圧} \\ &Y: \begin{cases} 1 ~~ {\small (薬\mathrm{A})} \\ 0 ~~ {\small (薬\mathrm{B})} \end{cases} \end{aligned} $$
すると、$E^X[X]$は『薬Aを内服した患者さんと薬Bを内服した患者さんを合算した全患者さん、における血圧の平均』となる。
一方で、$E^Y[E^{X|Y}[X|Y]]$は『薬Aを内服した患者さんにおける血圧の平均と、薬Bを内服した患者さんにおける平均の、重みづけ平均』となる。
1-2. 『期待値のくり返しの公式』のイメージFig
『期待値のくり返しの公式』のイメージFigは以下Fig1の様になります。
Fig1.
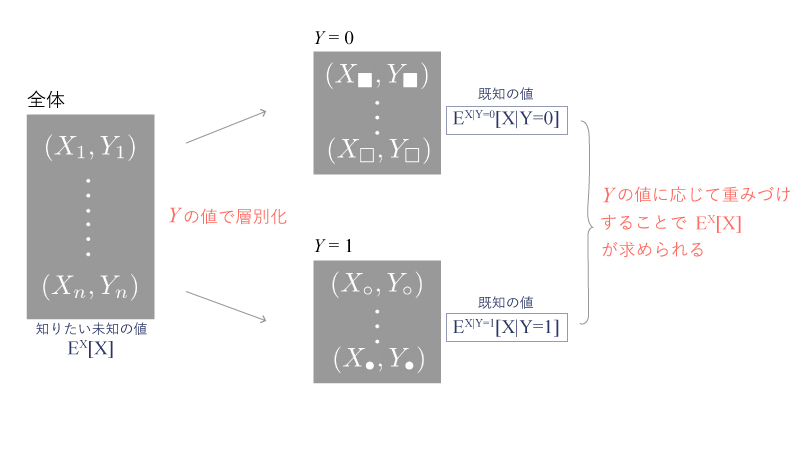
例1, 2とともにこのイメージFigも頭の中にいれておいてください!
1-3. 『期待値のくり返しの公式』の証明
(証明)
$X, Y$を(連続型の*)確率変数とし、($X,Y$の同時確率密度関数)、($X$の確率密度関数)、($Y$の確率密度関数)をそれぞれ、$f_{X, Y}(x, y), f_X(x), f_Y(y)$とする。
(*:ここでは連続型の確率変数を扱ったが、離散型の確率変数の場合には$\displaystyle \int$を$\sum$に変更するだけである)
この時、$$ \begin{aligned} E^X[X] &= \iint x \cdot f_{X, Y}(x, y) dxdy \\[10px] &= \int \left( \int x \cdot \frac{f_{X, Y}(x, y)}{f_Y(y)} dx\right) \cdot f_Y(y) dy \\[10px] &= \int E^{X|Y}[X|Y=y] \cdot f_Y(y) dy \\[10px] &= E^Y[E^{X|Y}[X|Y]] \end{aligned}$$ となる。
まとめ.
- 期待値のくり返しの公式 $$ \begin{aligned} E^X[X] = E^Y[ E^{X|Y}[X|Y] ] \end{aligned}$$





