$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}} \\ \gdef \tr {\mathrm{tr}}$
医学研究の分野だと、ポアソン回帰モデルは一定期間内における入院回数などに対して、ロジスティック回帰モデルは入院中の死亡などに対してよく用いられますね。
そうですね。
さて、今回の流れとしては、
①ポアソン回帰モデル
②ロジスティック回帰モデル
③一般化線形モデル
においてそれぞれの対数尤度関数の導出までを行います。
対数尤度関数をそれぞれの分布パラメータで微分して$=0$とした式を解析的に解くのは困難であり、フィッシャー・スコア法などで数値的に解くことになります。
④最尤推定量の導出
ではそれを簡単に紹介します。
1. ポアソン回帰
(ある観測事象の)単位時間あたりの発生回数$Y$に対して、
①(分布の仮定)
$$\begin{aligned} &\textcolor{red}{Y_i \sim \Po(\lambda_i)} ~~ {\small(i=1, \cdots, n)} \\ &{\scriptsize(即ち、確率関数f(y_i;\lambda_i) = \frac{e^{-\lambda_i} \lambda_i^{y_i}}{y_i!})} \\ &{\scriptsize(ただし、 \textcolor{red}{Y_i ~~ {\small(i=1, \cdots, n)}はそれぞれ独立} ) } \end{aligned}$$
②(分布パラメータの仮定)
$$\begin{aligned} \color{red}{\log \lambda_i} &= \beta_1 x_{i,1} + \cdots + \beta_d x_{i,d} ~~ {\small(i=1, \cdots, n)} \\ &{\scriptsize(ただし、(x_{1,1},\cdots,x_{n,1})^{\top} = \vec 1、つまり\beta_1が切片項とする)} \end{aligned}$$を仮定するモデルが『ポアソン回帰モデル』です。
尤度関数$L(\vec \beta)$、対数尤度関数$l(\vec \beta)$は、
$$\begin{aligned} L(\vec \beta) =& \prod_{i=1}^{n} (\frac{e^{-\lambda_i} \lambda_i^{y_i}}{y_i!}) \\ &{\scriptsize(Y_iの独立性より)} \\ \Rightarrow l(\vec \beta) =& \log L(\vec \beta) \\ =& \sum_{i=1}^{n} (\frac{e^{-\lambda_i} \lambda_i^{y_i}}{y_i!}) \\ =& \sum_{i=1}^{n} (-\lambda_i + y_i \log \lambda_i-\log y_i!) \\ =& \sum_{i=1}^{n} \{ -\exp(\beta_1 x_{i,1} + \cdots + \beta_d x_{i,d}) \\ &+ y_i (\beta_1 x_{i,1} + \cdots + \beta_d x_{i,d})-\log y_i! \} \end{aligned}$$となります。
2. ロジスティック回帰
$2$値変数$\{ 0,1 \}$のいずれかをとる観測事象の値$Y$に対して、
①(分布の仮定)
$$\begin{aligned} &\textcolor{red}{Y_i \sim \Bern(\pi_i)} ~~ {\small(i=1, \cdots, n)} \\ &{\scriptsize(即ち、確率関数f(y_i;\pi_i) = \pi_i^{y_i} (1-\pi_i)^{1-y_i} )} \\ &{\scriptsize(ただし、 \textcolor{red}{Y_i ~~ {\small(i=1, \cdots, n)}はそれぞれ独立} ) } \end{aligned}$$
②(分布パラメータの仮定)
$$\begin{aligned} \color{red}{\log \frac{\pi_i}{1-\pi_i}} &= \beta_1 x_{i,1} + \cdots + \beta_d x_{i,d} ~~ {\small(i=1, \cdots, n)} \\ &{\scriptsize(ただし、(x_{1,1},\cdots,x_{n,1})^{\top} = \vec 1、つまり\beta_1が切片項とする)} \end{aligned}$$を仮定するモデルが『ロジスティック回帰モデル』です。
尤度関数$L(\vec \beta)$、対数尤度関数$l(\vec \beta)$は、
$$\begin{aligned} L(\vec \beta) =& \prod_{i=1}^{n} (\pi^{y_i} (1-\pi_i)^{1-y_i}) \\ &{\scriptsize(Y_iの独立性より)} \\ \Rightarrow l(\vec \beta) =& \log L(\vec \beta) \\ =& \sum_{i=1}^{n} (\pi^{y_i} (1-\pi_i)^{1-y_i}) \\ =& \sum_{i=1}^{n} (y_i \log \pi_i + (1-y_i) \log(1-\pi_i) ) \\ =& \sum_{i=1}^{n} (y_i \log(\frac{\pi_i}{1-\pi_i}) + \log(1-\pi_i) ) \\ =& \sum_{i=1}^{n} (y_i \log(\frac{\pi_i}{1-\pi_i})-\log(1+\frac{\pi_i}{1-\pi_i}) ) \\ &{\scriptsize(\log(1-\pi_i) = -\log(\frac{1}{1-\pi_i}) = -\log(\frac{1-\pi_i}{1-\pi_i} + \frac{\pi_i}{1-\pi_i}) = -\log(1+\frac{\pi_i}{1-\pi_i}))} \\ =& \sum_{i=1}^{n} [ y_i (\beta_1 x_{i,1} + \cdots + \beta_d x_{i,d})-\log(1 + \exp(\beta_1 x_{i,1} + \cdots + \beta_d x_{i,d})) ] \end{aligned}$$となります。
3. 一般化線形モデル
これまで扱ってきた重回帰モデル、ポアソン回帰モデル、ロジスティック回帰モデルは『一般化線形モデル(GLM: Generalized Linear Model)』という枠組みで統一的に扱うことが可能です。
観測事象の値$Y$に対して、
①(分布の仮定)
$$\begin{aligned} &\textcolor{red}{f(y_i; \theta_i, \phi) = \exp \{ \frac{y_i \theta_i-b(\theta_i)}{a(\phi)}-c(y_i,\phi) \}} ~~ {\small(i=1, \cdots, n)} ~~~~~ \mathrm{(A)} \\ &{\scriptsize(ただし、\textcolor{red}{\mu_i = E[Y_i] }と定める ) } \\ &{\scriptsize(ただし、 \textcolor{red}{Y_i ~~ {\small(i=1, \cdots, n)}はそれぞれ独立} ) } \end{aligned}$$
②(分布パラメータの仮定)
$$\begin{aligned} \color{red}{ g(\mu_i)} &= \beta_1 x_{i,1} + \cdots + \beta_d x_{i,d} ~~ {\small(i=1, \cdots, n)} ~~~~~ \mathrm{(B)} \\ &{\scriptsize(ただし、(x_{1,1},\cdots,x_{n,1})^{\top} = \vec 1、つまり\beta_1が切片項とする)} \end{aligned}$$を仮定するモデルが『一般化線形モデル』です。
関数$g$は『リンク関数』と言い、単調性をもつ関数が採用されます。 単調性をもつ関数は逆関数をもつので、$\vec \beta$が与えられた時、
$$\begin{aligned} \mu_i = g^{-1}(\beta_1 x_{i,1} + \cdots + \beta_d x_{i,d}) \end{aligned}$$と$1$つに定まります。
また『$\theta_i$と$\mu_i$は1:1対応(結果のみ)』であるため、$\mu_i$が与えられた時、$\theta_i$は$1$つに定まります。 つまり、$\theta_i$は$\vec \beta$の関数です。
対数尤度関数は、
$$\begin{aligned} &\log \prod_{i=1}^n f(y_i; \theta_i, \phi) \\ &= {\small(\vec \betaと\phiの関数)} \\ &{\scriptsize(\theta_iは\vec \betaの関数であるため)} \end{aligned}$$より$l(\vec \beta, \phi)$と書くことができます。
(『1. ポアソン回帰』『2. ロジスティック回帰』では対数尤度関数は$l(\vec \beta)$と書きましたが、これは『①分布の仮定』において実質的に$\phi$がなかったためです)
なお、対数尤度関数$l(\vec \beta, \phi)$を$\vec \beta$で偏微分してみると、
$$\begin{aligned} \frac{\partial l(\vec \beta, \phi)}{\partial \vec \beta} &= \frac{\partial \theta_i}{\partial \vec \beta} \cdot \frac{\partial l(\vec \beta, \phi)}{\partial \theta_i} \\ &= \frac{\partial \theta_i}{\partial \vec \beta} \cdot \frac{\partial}{\partial \theta_i} \sum_{i=1}^n f(y_i; \theta_i, \phi) \\ &= \frac{\partial \theta_i}{\partial \vec \beta} \cdot \frac{\sum_{i=1}^n (y_i-b^{\prime}(\theta_i))}{a(\phi)} \end{aligned}$$となり、これを$= \vec 0$とすると、
$$\begin{aligned} \frac{\partial \theta_i}{\partial \vec \beta} \cdot \frac{\sum_{i=1}^n (y_i-b^{\prime}(\theta_i))}{a(\phi)} &= \vec 0 \\ \Rightarrow \frac{\partial \theta_i}{\partial \vec \beta} \cdot \sum_{i=1}^n (y_i-b^{\prime}(\theta_i)) &= \vec 0 \end{aligned}$$となり、この式に$\phi$は関与しません。
よって、この式のみから最尤推定値$\hat{\vec \beta}$は求まります。
(補足)
- $\mathrm{(A)}$は指数型分布族の形に似ています。実は$\mathrm{(A)}$は$\phi$がfixされている場合には指数型分布族となりますが、$\phi$がfixされていない場合には指数型分布族ではありません。
- $\mathrm{(A)}$から、$E[Y_i] = b'(\theta_i), V[Y_i] = b^{”}(\theta_i) a(\phi)$、が導かれます。
これまで扱ってきた重回帰モデル、ポアソン回帰モデル、ロジスティック回帰モデルが本当に一般化線形モデルの枠組みに入るのか納得できていません。。
それでは以下例を通じてそれを確認していきましょう。
例1. 重回帰モデル
$\mathrm{(A),(B)}$において、
$$\begin{aligned} \begin{cases} \theta_i &= \mu_i \\ \phi &= \sigma^2 \\ a(\phi) &= \phi \\ b(\theta_i) &= \dfrac{\theta_i^2}{2} \\ c(y_i, \phi) &= \dfrac{y^2}{2 \phi} + \dfrac{1}{2} \log (2 \pi \phi) \\ g(\mu_i) &= \mu_i \end{cases} \end{aligned}$$とおくと、
$$\begin{aligned} \begin{cases} f(y_i; \theta_i, \phi) &= \dfrac{1}{\sqrt{2 \pi \sigma^2}} \exp (-\dfrac{|y_i-\mu|^2}{2 \sigma^2}) \\ &{\scriptsize(①(分布の仮定))} \\ \mu_i &= \beta_1 x_{i,1} + \cdots + \beta_d x_{i,d} \\ &{\scriptsize(②(分布パラメータの仮定))} \end{cases} \end{aligned}$$となる。
例2. ポアソン回帰モデル
$\mathrm{(A),(B)}$において、
$$\begin{aligned} \begin{cases} \theta_i &= \log \mu_i \\ a(\phi) &= 1 \\ b(\theta_i) &= e^{\theta_i} \\ c(y_i, \phi) &= \log y_i! \\ g(\mu_i) &= \log \mu_i \end{cases} \end{aligned}$$とおくと、
$$\begin{aligned} \begin{cases} f(y_i; \theta_i, \phi) &= \dfrac{\mu_i^{y_i} e^{-\mu_i}}{y_i!} \\ &{\scriptsize(①(分布の仮定))} \\ \log \mu_i &= \beta_1 x_{i,1} + \cdots + \beta_d x_{i,d} \\ &{\scriptsize(②(分布パラメータの仮定))} \end{cases} \end{aligned}$$となる。
(注意:統一的に話を進めるために分布パラメータは$\mu$のままとしていますが、『1. ポアソン回帰』に話をあわせるとなると$\mu = \pi$とおくことになります)
例3. ロジスティック回帰モデル
$\mathrm{(A),(B)}$において、
$$\begin{aligned} \begin{cases} \theta_i &= \log \dfrac{\mu_i}{1-\mu_i} \\ a(\phi) &= 1 \\ b(\theta_i) &= \log (1 + e^{\theta_i}) \\ c(y_i, \phi) &= 0 \\ g(\mu_i) &= \log \dfrac{\mu_i}{1-\mu_i} \end{cases} \end{aligned}$$とおくと、
$$\begin{aligned} \begin{cases} f(y_i; \theta_i, \phi) &= \mu_i^{y_i} (1-\mu_i)^{1-y_i} \\ &{\scriptsize(①(分布の仮定))} \\ \log \dfrac{\mu_i}{1-\mu_i} &= \beta_1 x_{i,1} + \cdots + \beta_d x_{i,d} \\ &{\scriptsize(②(分布パラメータの仮定))} \end{cases} \end{aligned}$$となる。
(注意:統一的に話を進めるために分布パラメータは$\mu$のままとしていますが、『2. ロジスティック回帰』に話をあわせるとなると$\mu = \pi$とおくことになります)
各モデルにおける$\theta_i, a(\phi)$などの設定を覚える必要は一切ありません。重要なのは、これまで扱ってきた代表的なモデルは一般化線形モデルの枠組みで統一的に扱うことができ、その際には①観測データ$Y$が従う分布、②リンク関数、を決めれば良いということです。
主な統計ソフトでは各モデルに対するパッケージを使うこともできるし、一般化線形モデルのパッケージにおいて①②を指定することで各モデルを使うことも可能です。
4. 最尤推定量の導出
(注意:対数尤度関数$l(\vec \beta, \phi)$の$\vec \beta$についての最大化には$\phi$は関わってこないため、ここでは$l(\vec \beta, \phi)$を単純に$l(\vec \beta)$と記載します)
『1. ポアソン回帰モデル』『2. ロジスティック回帰モデル』『3. 一般化線形モデル』では対数尤度関数までを求めましたが、対数尤度関数をそれぞれの分布パラメータで微分して$=0$とした式を解析的に解くのは困難です。
そこでニュートン・ラフソン法やフィッシャー・スコア法を用いて、数値的に解くことになります。 『解析的に解く』とは、対数尤度関数をそれぞれの分布パラメータで微分して$=0$とした式を連立方程式で解くとうことです。一方の『数値的に解く*』とは以下Figのイメージで計算を進めるものです。
(*:コンピュータを用いて近似的に解く、というのが正確な解釈です。必ずしも以下の様に反復法を使ったものだけを数値的解法というわけではありません。)
Fig.
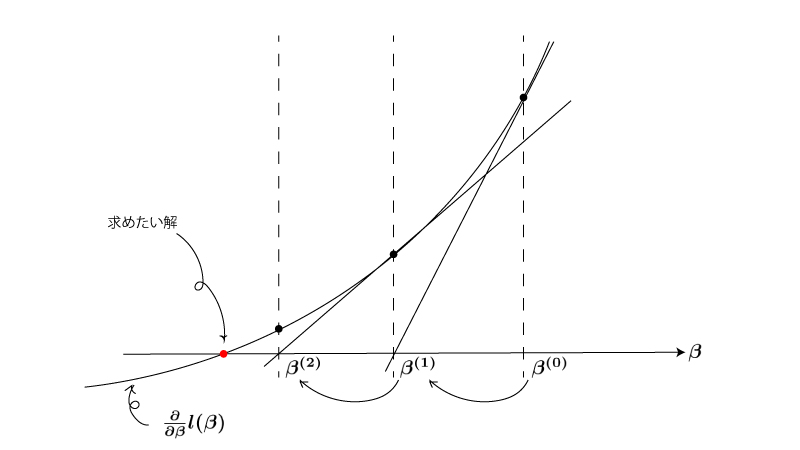
この曲線が対数尤度関数$l(\vec \beta)$を$\vec \beta$で微分した$\frac{\partial}{\partial \vec \beta} l(\vec \beta)$を表すものとすると、求めたい$\frac{\partial}{\partial \vec \beta} l(\vec \beta) = \vec 0$の解は赤丸の値となります。
(Figでは$1$次元の$\vec \beta$を扱っています)
ある$\vec \beta^{(0)}$から開始して、曲線の$\vec \beta = \vec \beta^{(0)}$における接線と$y=0$との交点の$\vec \beta$を$\vec \beta^{(1)}$とします。 続いて、曲線の$\vec \beta = \vec \beta^{(1)}$における接線と$y=0$との交点の$\vec \beta$を$\vec \beta^{(2)}$とします。 これを繰り返すと最終的には赤丸付近に到達します。
実際には$| \vec \beta^{(k+1)}-\vec \beta^{(k)} |$がある微小な値$\delta$を下回ったら更新を終了するという様なルールを定めておきます。
4-1. ニュートン・ラフソン法
上記で紹介した内容がニュートン・ラフソン法そのものになります。
つまり、以下の反復式を用いることになります。
$$\begin{aligned} \vec \beta^{(k+1)} = \vec \beta^{(k)}\textcolor{red}{-(\frac{\partial^2}{\partial \vec \beta^2} l(\vec \beta^{(k)}))^{-1}} (\frac{\partial}{\partial \vec \beta} l(\vec \beta^{(k)} )) \end{aligned}$$
上Figから、$\vec \beta^{(k+1)}-\vec \beta^{(k)}$、を計算してみると$-(\frac{\partial^2}{\partial \vec \beta^2} l(\vec \beta^{(k)}))^{-1} (\frac{\partial}{\partial \vec \beta} l(\vec \beta^{(k)}))$になることがわかります。つまりこの式は自然な式となります。
曲線の$\vec \beta = \vec \beta^{(k)}$における接線は、$y-\frac{\partial}{\partial \vec \beta} l(\vec \beta^{(k)}) =(\frac{\partial^2}{\partial \vec \beta^2} l(\vec \beta^{(k)})) (\vec \beta-\vec \beta^{(k)})$、であり、この式に$y=0$を代入した解$\vec \beta$が$\vec \beta^{(k+1)}$となることから導出できますね。
4-2. フィッシャー・スコア法
ニュートン・ラフソン法における赤文字部分$-(\frac{\partial^2}{\partial \vec \beta^2} l(\vec \beta^{(k)}))^{-1}$をその期待値(フィッシャー情報行列$I(\vec \beta^{(k)})$)で置換して、以下の反復式を用います。
$$\begin{aligned} \vec \beta^{(k+1)} = \vec \beta^{(k)}\textcolor{red}{+I(\vec \beta^{(k)})^{-1}} (\frac{\partial}{\partial \vec \beta} l(\vec \beta^{(k)})) \end{aligned}$$
こちらの反復式の方が計算が楽であることが多いです。なお、フィッシャー情報行列についてわからない方は<フィッシャー情報量>を参照ください。
まとめ.
- ポアソン回帰モデル、ロジスティック回帰モデルにおける【①(分布の仮定), ②(分布パラメータの仮定)】を確認した。
- 重回帰モデル、ポアソン回帰モデル、ロジスティック回帰モデルは一般化線形モデルの枠組みで統一的に扱うことができることを確認した。







