$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}} \\ \gdef \indep {\mathop{\perp\!\!\!\!\perp}} \\ \gdef \tr {\mathrm{tr}}$
1. サンプリングとは?
ここで言う『サンプリング』とは、標本抽出の文脈におけるものではなく、『ある分布に従う乱数を得る』ことを指します。
例. 標準正規分布$\N(0,1)$から乱数を得る場合
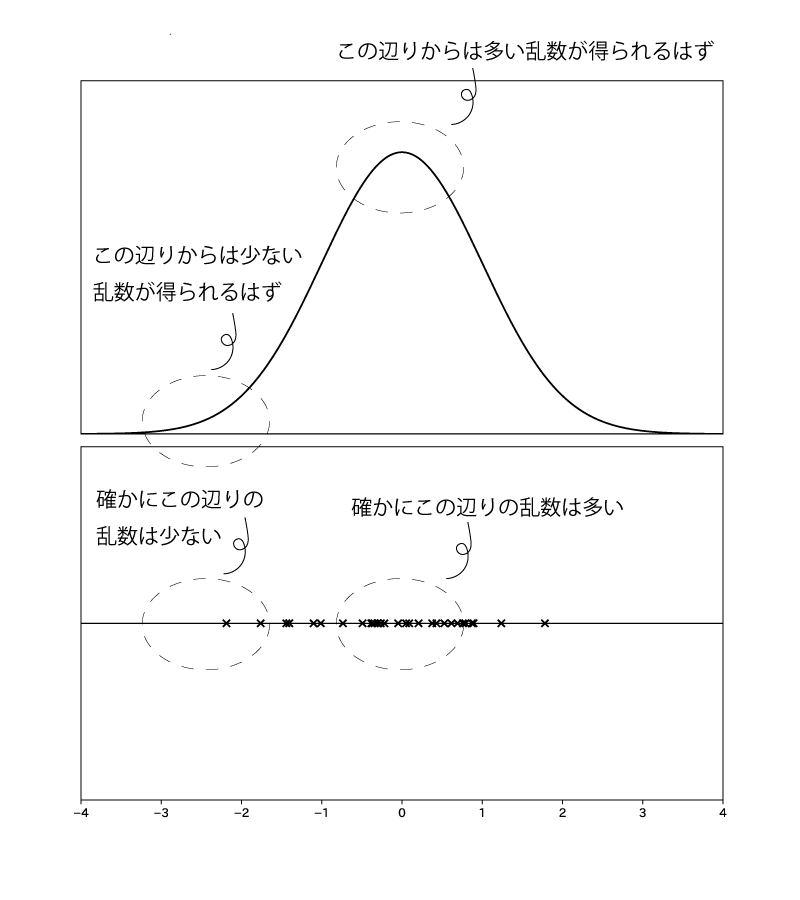
ところで、サンプリングによる嬉しさは何でしょうか?
それは、解析的に期待値計算をする(積分する)ことが困難な場合においても、サンプリングによって得られた乱数から近似的な期待値計算をすることができるということです。なお、サンプリングで得られた乱数による近似的な期待値計算を『モンテカルロ法』と言います。
ちょっとまだ具体的なイメージができてません。。
以下の補足でイメージを確立してください。
補足1.
『解析的な期待値計算』、『サンプリングで得られた乱数による近似的な期待値計算』について具体的にイメージできてない方も多いと思うので、以下確認していきます。
確率関数$X \sim \N(5,1)$とします。
つまり、確率密度関数$f(x)$が、
$$\begin{aligned} f(x) &= \frac{1}{\sqrt{2 \pi}} \exp [-\frac{(x-5)^2}{2}] ~~ \small{(-\infty \lt x \lt \infty)} \end{aligned}$$とします。
以下、ある関数$A()$を準備した上で、期待値$E[A(X)]$を計算するとします。
まず、$A(X) = X$、の場合を考えます。
$$\begin{aligned} E[A(X)] &= E[X] \\ &= \int_{-\infty}^{\infty} x f(x) dx \\ &= \int_{-\infty}^{\infty} x \cdot \frac{1}{\sqrt{2 \pi}} \exp [-\frac{(x-5)^2}{2}] dx \end{aligned}$$となりますが、これを直接計算するのが『解析的な期待値計算』です。
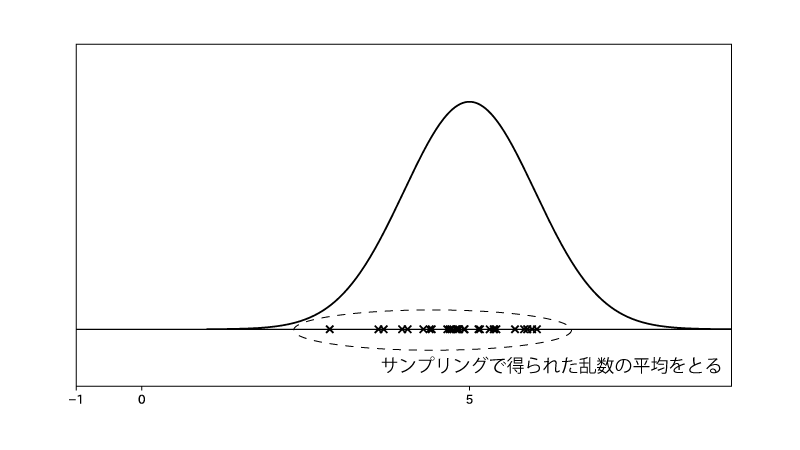
一方で、$X_1, \cdots, X_N \overset{i.i.d}\sim \N(5,1)$、と乱数を得た上で、
$$\begin{aligned} E[A(X)] &= E[X] \\ &\fallingdotseq \frac{1}{N} \sum_{k=1}^{N} X_k \end{aligned}$$と計算するのが『サンプリングで得られた乱数による近似的な期待値計算』です。
『サンプリングで得られた乱数による近似的な期待値計算』ではサンプリングで得られた乱数の平均をとってるのですね。
次に、$A(X)=\sin X$、の場合を考えます。
$$\begin{aligned} E[A(X)] &= E[\sin X] \\ &= \int_{-\infty}^{\infty} \sin x f(x) dx \\ &= \int_{-\infty}^{\infty} \sin x \cdot \frac{1}{\sqrt{2 \pi}} \exp [-\frac{(x-5)^2}{2}] dx \end{aligned}$$となりますが、これを直接計算するのが『解析的な期待値計算』です。
この計算は簡単にはできなさそうですね。。
一方で、$X_1, \cdots, X_N \overset{i.i.d}\sim \N(5,1)$、と乱数を得た上で、
$$\begin{aligned} E[A(X)] &= E[\sin X] \\ &\fallingdotseq \frac{1}{N} \sum_{k=1}^{N} \sin X_k \end{aligned}$$と計算するのが『サンプリングで得られた乱数による近似的な期待値計算』です。
ここまでは分布として$\N(5,1)$という『解析的な期待値計算』がかろうじて可能そうな分布を扱いました。
しかしながら『解析的な期待値計算』が到底不可能である分布についても、その分布からのサンプリングは比較的容易であることが多く、故に『サンプリングで得られた乱数による近似的な期待値計算』が可能であることが多いです。
ベイズ統計の事後分布は複雑な形になることが多く、『解析的な期待値計算』が到底不可能であることが多いです。
補足2.
$X_1, \cdots, X_N \overset{i.i.d}\sim \F$、と乱数を得た上で(ただし分布$\F$の確率密度関数を$f(x)$とする)、
$$\begin{aligned} E[A(X)] (&= \int A(x) f(x) dx )\\ &\fallingdotseq \frac{1}{N} \sum_{k=1}^{N} A(X_k) \end{aligned}$$と近似計算できるとしてました。
これは大数の法則から、
$$\begin{aligned} \frac{1}{N} \sum_{k=1}^{N} A(X_k) \overset{\displaystyle {p}}\longrightarrow E[A(X)] \end{aligned}$$が成立することを根拠としています。
(”$\overset{\displaystyle {p}}\longrightarrow$”は確率収束を表します。こちらがわからないかたは<極限定理>を参照ください。)
2. 具体的なサンプリング法
サンプリング法には沢山の種類がありますが、ここでは代表的なものを紹介します。
●逆関数法
●受容棄却法
●MCMC
2-1. 逆関数法
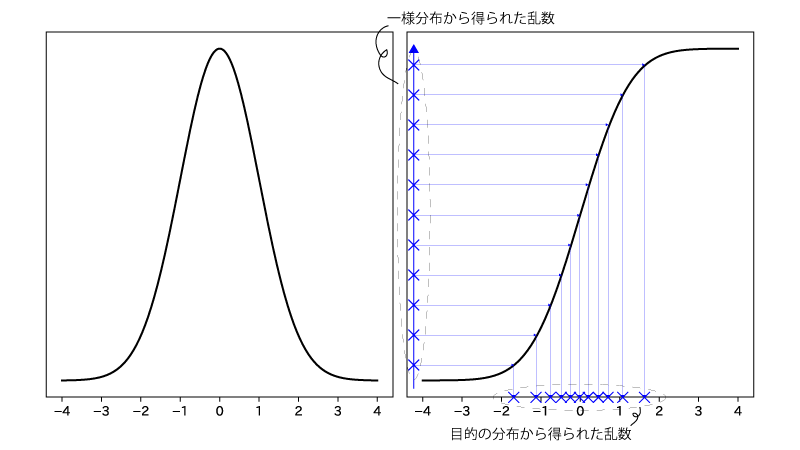
逆関数法では、目的の分布の分布関数(累積分布関数)の逆関数$F^{-1}$を用いて乱数を生成します。
具体的には、まず一様分布に従う乱数を生成し、その乱数を$F^{-1}$に入力することで目的の乱数を得ます。
2-2. 受容棄却法
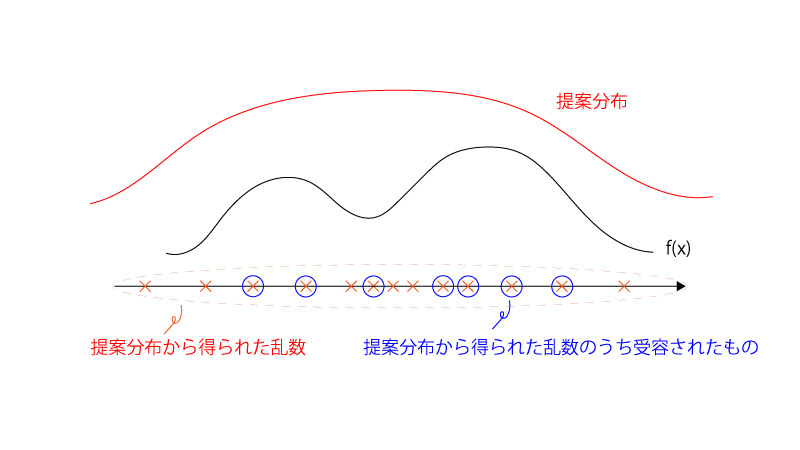
受容棄却法では、目的の分布$f(x)$を上から覆うことができる別の分布(『提案分布』という)から乱数を生成し、条件に応じてその乱数を受容するか棄却するかを決定することで、最終的な乱数が得られます。
2-3. MCMC
MCMCとは”Markov chain Monte Carlo”の略であり、日本語で言うと『マルコフ連鎖を用いたモンテカルロ法』です。(マルコフ連鎖がわからない方は<マルコフ連鎖>を参照ください)
MCMCでは、目的の分布が定常分布になる様にマルコフ連鎖を設定することで乱数を得ます。
MCMCを初めて聞いた方はこれだけではイメージがわかないかと思いますが、マルコフ連鎖によって逐次的にサンプリングされていく様なイメージだけ持っていただければ結構です。
MCMCの中には、
○MH(Metropolis–Hastings)
○GS(Gibbs sampling)
といった細かい手法があります。
2-4. 代表的なサンプリング法の使い分け
まず、目的の分布の分布関数の逆関数を陽に書くことができれば逆関数法で構いません。
もし、それができなければ受容棄却法で構いません。
ただし、受容棄却法では提案分布を準備する必要がありますが、適切な提案分布が見つからなかったり、確率ベクトルの次元が大きくなった時に効率的なサンプリングができないという問題があります。
そういった場合には、汎用的なサンプリング法であるMCMCが使えます。
そもそもすべてMCMCでよいのでは?と思われるかもしれませんが、状況や手間に応じてサンプリング法を決めるのが実際のところです。







