デルタ法

• 「1-1. デルタ法の説明」とのつながりがわからなくなった方もいるかもしれませんが、 $W \sim \mathrm{N}(0, \sigma^2)$とすれば$g^{\prime}(\mu)W \sim \mathrm{N}(0, \{ g^{\prime}(\mu) \}^2 \sigma^2)$となっており、上記はデルタ法を応用したものとわかります。
  
  
• 中心極限定理によると、
  確率変数列$\{ X_n \}$に対して、$X_i \overset{i.i.d}\sim F~~(E[X_i] = \mu, V[X_i] = \sigma^2) ~ {\small (i=1, \ldots, n)}$である時、
  $$ \begin{aligned} \displaystyle \frac{\bar{X_n} – \mu}{\displaystyle \frac{\sigma}{\sqrt n}} &\overset{\displaystyle {d}}\longrightarrow \mathrm{N}(0, 1) \\[20px] \Rightarrow \displaystyle \frac{\bar{X_n} – \mu}{\displaystyle \frac{1}{\sqrt n}} &\overset{\displaystyle {d}}\longrightarrow \mathrm{N}(0, \sigma^2) \\[20px] \Rightarrow \sqrt n (\bar{X_n} – \mu) &\overset{\displaystyle {d}}\longrightarrow \mathrm{N}(0, \sigma^2) \end{aligned}$$
  でした。（参照：＜極限定理＞：「4. 中心極限定理」）
  
  これは$\mathrm{(A)}$において$U_n = \bar{X_n}$とおいたものになっています。
  （より一般には、$U_n$は『漸近正規性をもつ量』（後出の最尤推定量など）とみることができます）

例題1.
確率変数列$\{ X_n \}$に対して、$X_i \overset{i.i.d}\sim F ~~ (E[X_i] = \mu, V[X_i] = \sigma^2) ~ {\small (i=1, \ldots, n)}$であるとする。
この時、$\sqrt n ( \bar{X_n}^2 – \mu^2)$の分布収束先を求めよ。
（ただし$\bar{X_n} = \displaystyle \frac{1}{n} \sum_{i=1}^n X_i$）

解答.
中心極限定理より、
$$ \begin{aligned} \sqrt n (\bar{X_n} – \mu) &\overset{\displaystyle {d}}\longrightarrow \mathrm{N}(0, \sigma^2) \end{aligned}$$が成立する。


ここで$g(X) = X^2$とすると、$g^{\prime}(X) = 2 X$である。


よってデルタ法より、
$$ \begin{aligned} \sqrt n (g(\bar{X_n}) – g(\mu)) &\overset{\displaystyle {d}}\longrightarrow \mathrm{N}(0, \{ g^{\prime}(\mu) \}^2\sigma^2) \\ \Rightarrow \sqrt n (\bar{X_n}^2 – \mu^2) &\overset{\displaystyle {d}}\longrightarrow \mathrm{N}(0, 4 \mu^2 \sigma^2) \end{aligned}$$

（示すべき内容）
確率変数列$\{ U_n \}$、確率変数$W$、定数$\theta$、数列$a_n$（ただし$a_n \to \infty ~ {\small (n \to \infty)}$）に対して、

$$ \begin{aligned} a_n (U_n – \theta) \overset{\displaystyle {d}}\longrightarrow W \end{aligned}$$
である時、連続微分可能な関数$g$（ただし$g^{\prime}(\theta)$が存在し$g^{\prime}(\theta) \neq 0$）に対して、

$$ \begin{aligned} a_n (g(U_n) – g(\theta)) \overset{\displaystyle {d}}\longrightarrow g^{\prime}(\theta) W \end{aligned}$$

（証明）

以下のFig1を考える。

Fig1.

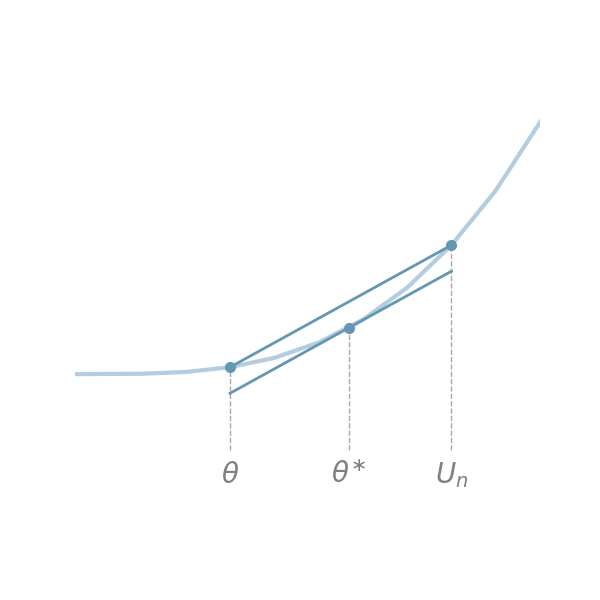
$U_n, \theta$の間にある$\theta \ast$に対して、Fig中の2直線の傾きの一致から、$$ \begin{aligned} \frac{g(U_n) – g(\theta)}{U_n – \theta} &= g^{\prime}(\theta^{\ast}) \\ \Rightarrow g(U_n) – g(\theta) &= g^{\prime}(\theta^{\ast})(U_n – \theta) ~~~~~\mathrm{(C)} \end{aligned}$$が成立する。


よって、$$\begin{aligned} a_n (g(U_n) – g(\theta)) &= a_n g^{\prime}(\theta^{\ast})(U_n – \theta) \\ &= g^{\prime}(\theta^{\ast}) \{ a_n (U_n – \theta) \} ~~~~~\mathrm{(D)} \end{aligned}$$となるので、以下右辺の分布収束先を考える。


$\mathrm{(D)}$内の$(U_n – \theta)$に注目して、$$ \begin{aligned} &U_n – \theta = (\frac{1}{a_n}) \cdot a_n(U_n – \theta) \overset{\displaystyle {d}}\longrightarrow 0 \cdot W = 0 \\ &{\scriptsize (仮定とスルツキーの定理から。＜補足. スルツキーの定理＞）} \end{aligned}$$ $$ \begin{aligned} \Rightarrow U_n – \theta \overset{\displaystyle {p}}\longrightarrow 0 \end{aligned}$$ $$ \begin{aligned} {\scriptsize (分布収束先が定数であるため同じ定数に確率収束する。＜補足. 確率収束と分布収束の関係＞）} \end{aligned}$$ $$\begin{aligned} \Rightarrow U_n \overset{\displaystyle {p}}\longrightarrow \theta \end{aligned}$$となる。


$\theta^{\ast}$は$U_n, \theta$の間にあるので、$$ \begin{aligned} \theta^{\ast} \overset{\displaystyle {p}}\longrightarrow \theta \end{aligned}$$となり、$g^{\prime}$が連続関数であるから、$$\begin{aligned} g^{\prime}(\theta^{\ast}) \overset{\displaystyle {p}}\longrightarrow g^{\prime}(\theta) ~~~~~\mathrm{(E)} \\ {\scriptsize (＜補足. 確率収束と分布収束の関係＞)} \end{aligned}$$となる。


よって$\mathrm{(D), (E)}$とスルツキーの定理より、$$ \begin{aligned} a_n (g(U_n) – g(\theta)) \overset{\displaystyle {d}}\longrightarrow g^{\prime}(\theta) W \end{aligned}$$が成立する。


（参照：＜補足. スルツキーの定理＞、＜補足. 確率収束と分布収束の関係＞）

（解答にでてくる記号を引き継ぐ）
$g(X)$を$\mu$まわりでTaylor展開すると、
$$ \begin{aligned} g(X) &= g(\mu) + \frac{g^{\prime}(\mu)}{1!}(X – \mu) + \frac{g^{\prime\prime}(\mu)}{2!}(X – \mu)^2 + \cdots \\ &\fallingdotseq g(\mu) + \frac{g^{\prime}(\mu)}{1!}(X – \mu)~~~~~\mathrm{(F)} \end{aligned}$$
両辺について期待値、分散をとると、
$$ \begin{aligned} E[g(X)] &\fallingdotseq g(\mu) \\ V[g(X)] &\fallingdotseq (g^{\prime}(\mu))^2 \cdot V[X] \\ &= (g^{\prime}(\mu))^2 \cdot \sigma^2 \end{aligned}$$

• この結果は例題1の解答と一致していますね！
  実は$\mathrm{(F)}$（Taylor展開で1次の項までの採用）は、「1-3. デルタ法の証明」における$\mathrm{(C)}$と同等です。
  
  というのも$\mathrm{(C)}$の$\theta$を$\mu$に置換した式は、$$\begin{aligned} g(U_n) &= g(\mu) + g^{\prime}(\mu^{\ast})(U_n – \mu) \\ &\fallingdotseq g(\mu) + g^{\prime}(\mu)(U_n – \mu) \\ &{\scriptsize (「1-3. デルタ法の証明」よりg^{\prime}(\mu^{\ast}) \overset{\displaystyle {p}}\longrightarrow g^{\prime}(\mu)でした)} \end{aligned}$$となっているからです。
  
  
• さらに少しだけつっこんで説明します。$$ \begin{aligned} \sqrt n \{ g(U_n) – g(\mu) \} &= \sqrt n \{ \frac{g^{\prime}(\mu)}{1!}(U_n – \mu) + \frac{g^{\prime\prime}(\mu)}{2!}(U_n – \mu)^2 + \cdots \} \\ &\overset{\displaystyle {d}}\longrightarrow {\small (ある確率変数)} \end{aligned}$$となっているので、右辺の$\{\}$内の$(U_n – \mu)$はおおよそ$\displaystyle \frac{1}{\sqrt n}$と同じスピードで収束する必要があります。（もし例えば$(U_n – \mu)$がおおよそ$\displaystyle \frac{1}{n^{\frac{1}{4}}}$と同じスピードで収束するとした場合、右辺はおおよそ$n^{\frac{1}{4}}$と同じスピードで発散することになるため、ある確率変数には収束できません）
  
  すると、右辺の$\{\}$内の第2項以降はおおよそ$(\displaystyle \frac{1}{\sqrt n})^2$と同じスピードで収束することになり、第1項に対して無視できることになります。

まとめ.

• デルタ法とは、（ある分布に分布収束することがわかっている）確率変数$X$と微分可能な連続関数$g$に対して、$g(X)$の分布収束先を求める方法である。
  
  
• デルタ法のよくある応用例として以下：
  $\sqrt n (U_n – \mu) \overset{\displaystyle {d}}\longrightarrow \mathrm{N}(0, \sigma^2)$、ならば $\sqrt n (g(U_n) – g(\mu)) \overset{\displaystyle {d}}\longrightarrow \mathrm{N}(0, \{ g^{\prime}(\mu) \}^2 \sigma^2)$