$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}}$
今回は(<推定量の性質>で扱った)「不偏性」をもつ推定量、即ち「不偏推定量」を扱います。
真の分布パラメータを$\theta$とした時、不偏推定量$\hat{\theta}_n$について$E[\hat{\theta}_n] = \theta$でしたね。
今回の概略を教えてください。
今回は、不偏推定量の中でより望ましい推定量、即ち、分散の小さい推定量、が主たるトピックです。
『不偏推定量の望ましさを比較するにあたって、分散が小さい方がよい』のでしょうか?
その通りです!ちなみに、不偏推定量の中で最も望ましい(分散が最小)推定量を「UMVU」と言います。この「UMVU」は非常に重要な概念で、今後もよく出てくるので覚えておいてください。
UMVU。。。
0. 不偏推定量
(真の分布パラメータを$\theta$として)
『ある推定量$\hat{\theta}_{n}$が不偏性をもつ(不偏推定量である)』とは、
$$\begin{aligned} E_{\theta}[\hat{\theta}_{n}] = \theta \end{aligned}$$が成立することでした。(参照:<推定量の性質>)
(注意)
$E_{\theta}[\hat{\theta}_{n}]$の右下添字”$_{\theta}$”は、期待値をとる時の分布パラメータが$\theta$であることを明示するためのものです。必ずしもつける必要はありませんが、今回はつける様に統一します。
1. バイアスとバリアンス
1-1. バイアスとバリアンスの定義
(定義)
(真の分布パラメータを$\theta$として)
推定量$\hat{\theta}_{n}$の「バイアス(偏り)」$b_{\theta}(\hat{\theta}_{n})$、「バリアンス(分散)」$V_{\theta}(\hat{\theta}_{n})$は、
$$\begin{aligned} b_{\theta}(\hat{\theta}_{n}) &= E_{\theta}[\hat{\theta}_{n}]-\theta \\[10px] V_{\theta}(\hat{\theta}_{n}) &= E_{\theta}[(\hat{\theta}_{n}-E_{\theta}[\hat{\theta}_{n}])^2] \end{aligned}$$と定義されます。
- 不偏推定量$\hat{\theta}_{n}$については、$E_{\theta}[\hat{\theta}_{n}]=\theta$より$b_{\theta}(\hat{\theta}_{n})=0$、となります。つまり、不偏推定量はバイアス$0$の推定量なのです。またバリアンスは新しい概念ではなく、これまで扱ってきた「分散」そのものです。
- バイアス、バリアンスのイメージFigは以下の様になります。
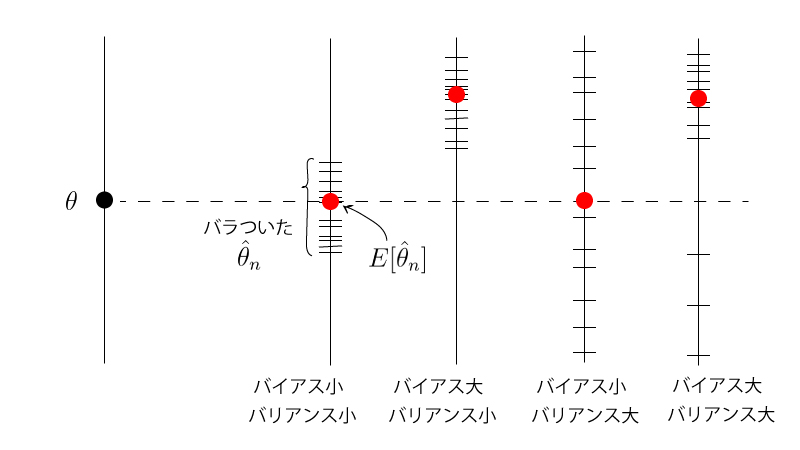
1-2. 平均2乗誤差とバイアス・バリアンス分解
1-2-1. 平均$2$乗誤差の定義
(定義)
(真の分布パラメータを$\theta$として)
推定量$\hat{\theta}_{n}$の「平均$2$乗誤差」$MSE[\theta, \hat{\theta}_{n}]$(MSE: Mean Squared Error)は、
$$\begin{aligned} MSE[\theta, \hat{\theta}_{n}] = E_{\theta}[(\hat{\theta}_{n}-\theta)^2] \end{aligned}$$と定義されます。
- 平均$2$乗誤差$MSE[\theta, \hat{\theta}_{n}]$は、真の分布パラメータ$\theta$を固定した時に、推定量$\hat{\theta}_{n}$との『離れ具合*』を平均化したものであり、『推定量としての望ましさ』を表す一般的指標です。
*:『離れ具合』を表す指標は他にもあります。(例:$E_{\theta}[|\hat{\theta}_{n}-\theta|]$)
1-2-2. (平均$2$乗誤差の)バイアス・バリアンス分解
以下の式が成立しています。
$$\begin{aligned} (MSE[\theta, \hat{\theta}_{n}]=) ~ E_{\theta}[(\hat{\theta}_{n}-\theta)^2] = (b_{\theta}(\hat{\theta}_{n}))^2 + V_{\theta}(\hat{\theta}_{n}) \end{aligned}$$
平均$2$乗誤差がバイアス・バリアンスからなる項に分解されるので、この式を『(平均$2$乗誤差の)バイアス・バリアンス分解』と言います。
(証明)
$$\begin{aligned} E_{\theta}[(\hat{\theta}_{n}-\theta)^2] &= E_{\theta}[\{(\hat{\theta}_{n}-E_{\theta}[\hat{\theta}_{n}]) + (E_{\theta}[\hat{\theta}_{n}]-\theta)\}^2] \\ &{\scriptsize (無理やりE_{\theta}[\hat{\theta}_{n}]を組み込んだ)} \\[10px] &= E_{\theta}[(\hat{\theta}_{n}-E_{\theta}[\hat{\theta}_{n}])^2] + 2 (E_{\theta}[\hat{\theta}_{n}]-\theta) \cdot E_{\theta}[\hat{\theta}_{n}-E_{\theta}[\hat{\theta}_{n}]] + (E_{\theta}[\hat{\theta}_{n}]-\theta)^2 \\[10px] &= V_{\theta}[\hat{\theta}_{n}] + 0 + (b_{\theta}(\hat{\theta}_{n}))^2 \\ &{\scriptsize (E_{\theta}[\hat{\theta}_{n}-E_{\theta}[\hat{\theta}_{n}]] = E_{\theta}[\hat{\theta}_{n}]-E_{\theta}[\hat{\theta}_{n}]=0)} \\[10px] &= (b_{\theta}(\hat{\theta}_{n}))^2 + V_{\theta}[\hat{\theta}_{n}] \end{aligned}$$
- バイアス・バリアンス分解が意味するところは、『推定量としての望ましさを表す平均$2$乗誤差は、推定量の偏り具合(バイアス)と散らばり具合(バリアンス)に分解される』ということです。
- 不偏推定量のバイアスは$0$なので、$\hat{\theta}_{n}$が$\theta$の不偏推定量である時、バイアス・バリアンス分解の式より、
$$\begin{aligned} E_{\theta}[(\hat{\theta}_{n}-\theta)^2] = V_{\theta}[\hat{\theta}_{n}] \end{aligned}$$となります。つまり、『不偏推定量という階級に限定した場合には、推定量としての望ましさを考えるにあたりバリアンスのみを考えればよい』ということです。
2. UMVU
(定義)
『不偏推定量$\hat{\theta}_{n}^{*}$がUMVU(Uniformly Minimum Variance Unbiased Estimator: 一様最小分散不偏推定量)』とは、任意の不偏推定量$\hat{\theta}_{n}$に対して、
$$\begin{aligned} V_{\theta}[\hat{\theta}_{n}^{*}] \leqq V_{\theta}[\hat{\theta}_{n}] ~~ (\textcolor{red}{\forall \theta}) \end{aligned}$$が成立することです。
つまりUMVUとは、不偏推定量という階級において最もバリアンスの小さい推定量、即ち最も望ましい推定量となります。
3. クラメル・ラオの不等式
確率ベクトル$\vec X=(X_1, \ldots, X_n)$の同時確率関数(同時確率密度関数)を$f_n(\vec x;\theta)$と表した時(ただし$\theta$は分布パラメータ)、フィッシャー情報量$I_n(\theta)$は
$$\begin{aligned} I_n(\theta) = E [ (\dfrac{\partial \log f_n(\vec X;\theta)}{\partial \theta})^2 ] ~(= E[-\dfrac{\partial^2 \log f_n(\vec X; \theta)}{\partial \theta^2}]) \end{aligned}$$となりました。
(参照:<フィッシャー情報量>:「性質1」)
フィッシャー情報量が正である時、不偏推定量$\hat{\theta}_{n}$に対して、
$$\begin{aligned} V_{\theta}[\hat{\theta}_{n}] \geqq \frac{1}{I_n(\theta)} ~~~~~ \mathrm{(A)} \end{aligned}$$が成立して、この不等式を「クラメル・ラオの不等式」と言います。
- クラメル・ラオの不等式は、不偏推定量のバリアンス(分散)とフィッシャー情報量の間に成立する式で、『不偏推定量の分散の最小値はフィッシャー情報量の逆数を下回らない』と主張するものです。
- $X_i \overset{i.i.d}\sim F~~{\small (i=1, \ldots, n)}$である時、$I_n(\theta) = n I_1(\theta)$であったので(参照:<フィッシャー情報量>:「性質2」)、$\mathrm{(A)}$は、
$$\begin{aligned} V_{\theta}[\hat{\theta}_{n}] \geqq \frac{1}{n I_1(\theta)} \end{aligned}$$と書き換えることができます。 - 証明はややテクニカルです。興味ある方は<補足. クラメル・ラオの不等式の証明>を参照してください。
よってサンプルサイズ$n$が大きくなると、クラメル・ラオの下限値$(\frac{1}{n I_1(\theta)})$が小さくなってゆくことがわかりますね。
4. ある不偏推定量がUMVUであることの示し方
ある不偏推定量がUMVUであることを示したい時、以下の$2$通りの方法が考えられます。
・①その推定量がクラメル・ラオの不等式の下限を達成することを示す
・②その推定量が完備十分統計量(またはその関数)であることを示す
- ①は、クラメル・ラオの不等式の主張(不偏推定量の分散の最小値はフィッシャー情報量の逆数を下回らない)とUMVUの定義(UMVUは不偏推定量の中で分散が最小)に基づくものです。
- ②は、『ある推定量が不偏推定量、かつ、完備十分統計量(またはその関数)であればその推定量はUMVU』という定理に基づくものです。(以下参照)
UMVUは統計検定$1$級の題材としてよく使われており、この$2$通りの示し方は必ず覚えておいてください。
(『ある推定量が不偏推定量、かつ、完備十分統計量(またはその関数)であればその推定量はUMVU』の証明)
『証明のための準備1』→『証明のための準備2』→『パート1』→『パート2』→『パート3』という流れで進めていきます。
(証明のための準備1:「ラオ・ブラックウェルの定理」)
「ラオ・ブラックウェルの定理」とは、 推定量$\hat{\theta}_{n}$、十分統計量$T$について、
$$\begin{aligned} \hat{\theta}_{n}^{*} = E_{\theta}[\hat{\theta}_{n}|T] \end{aligned}$$として新たな推定量$\hat{\theta}_{n}^{*}$を産み出した時、
$$\begin{aligned} E_{\theta}[(\hat{\theta}_{n}^{*}-\theta)^2] \leqq E_{\theta}[(\hat{\theta}_{n}-\theta)^2] ~~ (\textcolor{red}{\forall \theta}) \end{aligned}$$が成立する、という定理です。
ラオ・ブラックウェルの定理の主張は、『十分統計量を用いると推定量を改善できる(平均$2$乗誤差をより小さい推定量を産み出すことができる)』というものです。証明は<補足. ラオ・ブラックウェルの定理>を参照ください。
(証明のための準備2:完備十分統計量の関数である不偏推定量の一意性)
完備十分統計量$T$の関数である($\theta$の)不偏推定量$\hat{\theta}_{n}^{*}, \tilde{\theta}_{n}^{*}$に対して、
$$\begin{aligned} E_{\theta}[\underbrace{\hat{\theta}_{n}^{*}-\tilde{\theta}_{n}^{*}}_{=g(T)とする}] &= E_{\theta}[\hat{\theta}_{n}^{*}]-E_{\theta}[\tilde{\theta}_{n}^{*}] \\ &= \theta-\theta \\ &{\scriptsize (\hat{\theta}_{n}^{*}, \tilde{\theta}_{n}^{*}は\thetaの不偏推定量)} \\ &= 0 \end{aligned}$$となる。
$T$は完備十分統計量なのでその定義から、
$$\begin{aligned} (g(T)&=) ~ \hat{\theta}_{n}^{*}-\tilde{\theta}_{n}^{*} = 0 \\ &\Rightarrow \hat{\theta}_{n}^{*} = \tilde{\theta}_{n}^{*} \end{aligned}$$となる。
(パート$1$:任意の不偏推定量$\hat{\theta}_{n}$と完備十分統計量$T$から作成された推定量$E_{\theta}[\hat{\theta}_{n}|T]$は$\theta$の不偏推定量)
任意の($\theta$の)不偏推定量$\hat{\theta}_{n}$、完備十分統計量$T$に対して、
$$\begin{aligned} \hat{\theta}_{n}^{*} = E_{\theta}[\hat{\theta}_{n}|T] \end{aligned}$$とおくと、
$$\begin{aligned} E_{\theta}^{\vec X}[\hat{\theta}_{n}^{*}] &= E_{\theta}^{T}[E_{\theta}^{\vec X|T}[\hat{\theta}_{n}|T]] \\ &= E_{\theta}^{\vec X}[\hat{\theta}_{n}] \\ &{\scriptsize (期待値の繰り返しの公式を用いた)} \\ &= \theta \\ &{\scriptsize (\hat{\theta}_{n}は\thetaの不偏推定量)} \end{aligned}$$
(参照:<期待値の繰り返しの公式>) となるため、$\hat{\theta}_{n}^{*}$は$\theta$の不偏推定量である。
(パート$2$:$\hat{\theta}_{n}^{*}=E_{\theta}[\hat{\theta}_{n}|T]$が$\hat{\theta}_{n}$によらず一意に決まる)
産み出された$\hat{\theta}_{n}^{*}=E_{\theta}[\hat{\theta}_{n}|T]$は完備十分統計量$T$の関数、かつ、$\theta$の不偏推定量であったため、上記『完備十分統計量の関数である不偏推定量の一意性』により$\hat{\theta}_{n}$の取り方によらず一意に決まる。
(異なる不偏推定量$\tilde{\theta}_{n}, \check{\theta}_{n}$から生み出された$E_{\theta}[\tilde{\theta}_{n}|T], E_{\theta}[\check{\theta}_{n}|T]$は一致する)
(パート$3$:$\hat{\theta}_{n}^{*}=E_{\theta}[\hat{\theta}_{n}|T]$は平均$2$乗誤差(分散)を最小にする)
任意の$\theta$の不偏推定量$\tilde{\theta}_{n}$に対して、
$$\begin{aligned} E_{\theta}[(\tilde{\theta}_{n}-\theta)^2] &\geqq E_{\theta}[(E_{\theta}[\tilde{\theta}_{n}|T]-\theta)^2] \\ &{\scriptsize (ラオ・ブラックウェルの定理より)} \\ &= E_{\theta}[(\hat{\theta}_{n}^{*}-\theta)^2] \\ \Rightarrow V_{\theta}[\tilde{\theta}_{n}] \geqq V_{\theta}[\hat{\theta}^{*}_{n}] \\ &{\scriptsize (\hat{\theta}_{n}^{*}, \hat{\theta}_{n}はともに\thetaの不偏推定量)} \end{aligned}$$
例題1.
$X_i \overset{i.i.d} \sim \Po(\lambda)~~{\small (i=1, \ldots, n)}$である時、$\lambda$の不偏推定量$\hat{\lambda}_{n} = \frac{1}{n} \sum_{i=1}^{n} X_i$がUMVUであることを$2$通りの方法で示せ。
ただし$\Po(\lambda)$の確率関数$p(x)$は
$$\begin{aligned} p(x) = \frac{\lambda^x e^{-\lambda}}{x!} \end{aligned}$$である。
解答. (方法1. $\hat{\lambda}_{n}$がクラメル・ラオの不等式の下限を達成することを示す方法)
$\hat{\lambda}_{n}$の分散$V_{\lambda}[\hat{\lambda}_{n}]$がクラメル・ラオの不等式の下限に一致することを示す。
まずフィッシャー情報量$I_{1}(\lambda)$は、
$$\begin{aligned} I_{1}(\lambda) &= E_{\lambda}[- \frac{\partial^2 \log p(X)}{\partial \lambda^2}] \\[10px] &= E_{\lambda}[- \frac{\partial^2}{\partial \lambda^2} (X \log \lambda-\lambda-\log X!)] \\[10px] &= E_{\lambda}[\frac{X}{\lambda^2}] \\[10px] &= \frac{1}{\lambda} \\ &{\scriptsize (E_{\lambda}[X] = \lambda)} \end{aligned}$$となるから、$I_{n}(\lambda)$は、
$$\begin{aligned} I_n(\lambda) &= n I_1(\lambda) \\ &{\scriptsize (X_i (i=1, \ldots, n)の独立性より)} \\[10px] &= \frac{n}{\lambda} \end{aligned}$$となり、
$$\begin{aligned} {\small (クラメル・ラオの不等式の下限)} &= \frac{1}{I_n(\lambda)} \\[10px] &= \frac{\lambda}{n} \end{aligned}$$となる。
一方で$V_{\lambda}[\hat{\lambda}_{n}]$は、
$$\begin{aligned} V_{\lambda}[\hat{\lambda}_{n}] &= V_{\lambda}[\frac{1}{n} \sum_{i=1}^{n} X_i] \\[10px] &= (\frac{1}{n})^2 \cdot V_{\lambda}[\sum_{i=1}^{n} X_i] \\[10px] &= (\frac{1}{n})^2 \cdot n V_{\lambda}[X_i] \\ &{\scriptsize (X_i (i=1, \ldots, n)の独立性より)} \\[10px] &= \frac{\lambda}{n} \\ &{\scriptsize (V[X_i]=\lambda)} \end{aligned}$$となる。
よって$V_{\lambda}[\hat{\lambda}_{n}]$はクラメル・ラオの不等式の下限に一致するため、$\hat{\lambda}_{n}$はUMVUである。
解答. (方法2. $\hat{\lambda}_{n}$が完備十分統計量(またはその関数)であることを示す方法)
$\sum_{i=1}^{n} X_i$は$\lambda$の完備十分統計量であるから(参照:<完備十分統計量>:「例題2」)、
$\hat{\lambda}_{n} = \frac{1}{n} \sum_{i=1}^{n} X_i$は完備十分統計量の関数である。
よって$\hat{\lambda}_{n}$は($\lambda$の)不偏推定量、かつ、完備十分統計量の関数であるため、$\hat{\lambda}_{n}$はUMVUである。
まとめ.
- 推定量としての望ましさは平均$2$乗誤差に基づき、これはバイアス、バリアンスからなる項に分解される。
- 不偏推定量は(バイアス)$=0$なので、(平均$2$乗誤差)$=$(バリアンス)となり、バリアンスを最小とする推定量が最も望ましい。
- 不偏推定量の分散の最小はクラメル・ラオの不等式の下限であり、それはフィッシャー情報量の逆数である。
- ある不偏推定量がUMVUであることを示すには以下の$2$通りがある。
①その不偏推定量がクラメル・ラオの不等式の下限を達成することを示す
②その不偏推定量が完備十分統計量(またはその関数)であることを示す







