$\gdef \vec#1{\boldsymbol{#1}} \\ \gdef \rank {\mathrm{rank}} \\ \gdef \det {\mathrm{det}} \\ \gdef \Bern {\mathrm{Bern}} \\ \gdef \Bin {\mathrm{Bin}} \\ \gdef \Mn {\mathrm{Mn}} \\ \gdef \Cov {\mathrm{Cov}} \\ \gdef \Po {\mathrm{Po}} \\ \gdef \HG {\mathrm{HG}} \\ \gdef \Geo {\mathrm{Geo}}\\ \gdef \N {\mathrm{N}} \\ \gdef \LN {\mathrm{LN}} \\ \gdef \U {\mathrm{U}} \\ \gdef \t {\mathrm{t}} \\ \gdef \F {\mathrm{F}} \\ \gdef \Exp {\mathrm{Exp}} \\ \gdef \Ga {\mathrm{Ga}} \\ \gdef \Be {\mathrm{Be}} \\ \gdef \NB {\mathrm{NB}}$
今回は「連続分布」に該当する分布を$1$つずつ確認していきます。
【①確率密度関数、②特性値、③Fig】を各分布について確認していきましょう。
連続分布に属する分布も多いので大変ですね。なんとか乗り切りたいと思います!
がんばりましょう。<離散分布>の時と同じく、分布間の関係性を総括してから$1$つずつ分布を確認しましょう。
0. 連続分布に属する分布間の関係性
連続分布に属する主な分布間の関係性は以下のFig0の通りになっています。
Fig0.
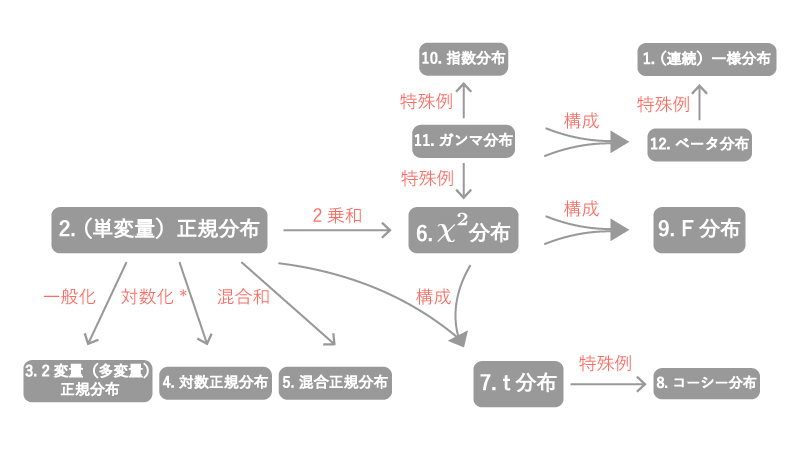
*:『対数化』とはあくまでイメージを表すものです
「②正規分布」「⑥$\chi^2$分布」が様々な分布との関係性をもつので、離散分布の中心に位置するとイメージするとよいかと思います。
以下各分布間の関係性を確認していきます。
0-1. 「②(単変量)正規分布」と「③2変量(多変量)正規分布」
(単一の)確率変数に対する正規分布が「(単変量)正規分布」、確率ベクトルに対する正規分布が「2変量(多変量)正規分布」です。
0-2. 「②正規分布」と「④対数正規分布」
$X \sim$ (対数正規分布)である時、$\log X \sim$(正規分布)、です。
0-3. 「②正規分布」と「⑤混合正規分布」
(混合正規分布) $= \pi_1 \cdot$(正規分布$1$) $\cdots + \pi_K \cdot$(正規分布$K$)、です。
(ただし、$\sum_{k=1}^K \pi_k = 1$)
0-4. 「②正規分布」と「⑥$\chi^2$分布」
$Z_i \overset{i.i.d}\sim \N(0, 1) ~~{\small (i=1, \ldots, n)}$である時、
$X = \sum_{i=1}^n Z_i^2$が従う分布が「(自由度$n$の)$\chi^2$分布」です。
0-5. 「⑥$\chi^2$分布」と「⑦$t$分布」
$X (\sim$ (自由度$n$の)$\chi^2$分布)$, ~ Z (\sim \N(0, 1))$が互いに独立である時、
$T = \displaystyle \frac{Z}{\sqrt{\frac{X}{n}}}$が従う分布が「(自由度$n$の)$t$分布」です。
0-6. 「⑥$\chi^2$分布」と「⑨$F$分布」
$X_1 (\sim$ (自由度$n_1$の)$\chi^2$分布)$, ~ X_2 (\sim$ (自由度$n_2$の)$\chi^2$分布)が互いに独立である時、
$X = \displaystyle \frac{\frac{X_2}{n_2}}{\frac{X_1}{n_1}}$が従う分布が「(自由度$(n_1, n_2)$の)$F$分布」です。
0-7. 「⑪ガンマ分布」と「⑥$\chi^2$分布」
$($自由度$(\frac{n}{2}, 2)$のガンマ分布$) = ($自由度$n$の$\chi^2$分布)、です。
0-8. 「⑪ガンマ分布」と「⑩指数分布」
$($自由度$(1, \frac{1}{\lambda})$のガンマ分布$) = ($パラメータ$\lambda$の指数分布$)$、です。
0-9. 「⑪ガンマ分布」と「⑫ベータ分布」
$X_1 \sim$((自由度$(a_1, b)$の)ガンマ分布)$, ~ X_2 \sim$ ((自由度$(a_2, b)$の)ガンマ分布)が互いに独立である時、
$X = \displaystyle \frac{X_1}{X_1 + X_2}$が従う分布が「自由度$(a_1, a_2)$のベータ分布」です。
0-10. 「⑫ベータ分布」と「①(連続)一様分布」
(自由度$(1, 1)$のベータ分布) $=$ ((連続)一様分布)、です。
- 各分布の定義をご存知ない方は、上記説明がわからないかと思いますので、引き続く各分布の説明を確認した後に再度上記を確認してみてください。最終的には上記Fig0はすらっと書き下せることが望ましいです。
- (離散分布と同じく)連続分布においても再生性・無記憶性をもつ分布があり、以下の通りです。
再生性をもつ分布:「②(単変量)正規分布」、「③2変量(多変量)正規分布」、「⑥$\chi^2$分布」、「⑪ガンマ分布」
無記憶性をもつ分布:「⑩指数分布」
少し整理できたでしょうか?
ここからは各分布について見ていきます。
1. (連続)一様分布
「確率変数$X$が分布パラメータ$(a, b)$の(連続)一様分布に従うこと」を
「$X \sim \U(a, b)$」と表します。(ただし、$a, b \in \mathbb{R}, a \lt b$で、$X$は区間$[a,b]$上の値をとります)
1-1. 確率密度関数
$$\begin{aligned} f(x) = \dfrac{1}{b-a} ~~ (a \leqq x \leqq b) \end{aligned}$$
1-2. 特性値
$$\begin{aligned} &{\small ①平均:}E[X] = \dfrac{1}{2} (a+b) \\ &{\small ②分散:}V[X] = \dfrac{1}{12} (b-a)^2 \\ &{\small ③積率母関数:}M^X(\theta) = \begin{cases} \dfrac{e^{b\theta} – e^{a\theta}}{(b-a)\theta} ~~ &{\small (\theta \neq 0)} \\[5px] 1 ~~ &{\small (\theta = 0)} \end{cases} \end{aligned}$$
(①〜③の証明はこちら:<補足. 連続分布_一様分布>)
1-3. Fig
Fig1. 確率密度関数
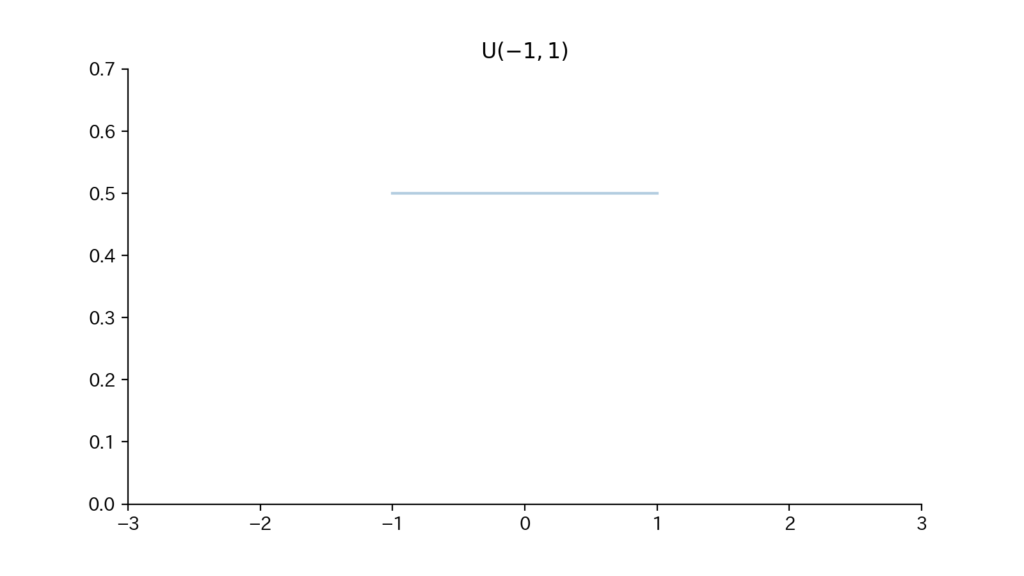
2. (単変量)正規分布
「確率変数$X$が分布パラメータ$(\mu, \sigma^2)$の(単変量)正規分布に従うこと」を
「$X \sim \N(\mu, \sigma^2)$」と表します。(ただし、$\mu \in \mathbb{R}, \sigma^2 \gt 0$)
2-1. 確率密度関数
$$\begin{aligned} f(x) = \dfrac{1}{\sqrt{2 \pi \sigma^2}} \exp[- \dfrac{(x-\mu)^2}{2\sigma^2}] ~~ (- \infty \lt x \lt \infty) \end{aligned}$$
2-2. 特性値
$$\begin{aligned} &{\small ①平均:}E[X] = \mu \\ &{\small ②分散:}V[X] = \sigma^2 \\ &{\small ③積率母関数:}M^X(\theta) = \exp [\mu \theta + \dfrac{1}{2}\sigma^2 \theta^2] \end{aligned}$$
(①〜③の証明はこちら:<補足. 連続分布_(単変量)正規分布>)
2-3. Fig
Fig2. 確率密度関数
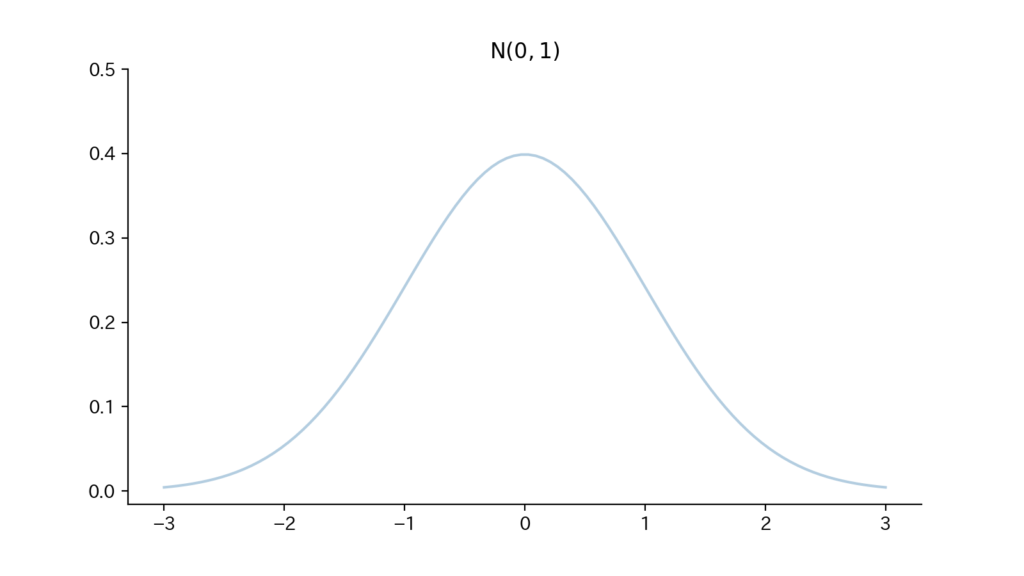
- 前述のとおり、正規分布には再生性があります。即ち、確率変数$X_1, X_2$が互いに独立に正規分布に従う時(注意:パラメータは異なっても構いません)、$(X_1 + X_2)$も正規分布に従います。
(証明)
$X_1 (\sim \N(\mu_1, \sigma_1^2)), ~X_2 (\sim \N(\mu_2, \sigma_2^2))$が互いに独立である時、それぞれの積率母関数$M^{X_1}(\theta), M^{X_2}(\theta)$について、
$$\begin{aligned} M^{X_1}(\theta) &= \exp [\mu_1 \theta + \dfrac{1}{2} \sigma_1^2 \theta^2] \\ M^{X_2}(\theta) &= \exp [\mu_2 \theta + \dfrac{1}{2} \sigma_2^2 \theta^2] \end{aligned}$$であるから、
$$\begin{aligned} M^{X_1 + X_2}(\theta) &= E[e^{\theta (X_1 + X_2)}] \\[5px] &= E[e^{\theta X_1}] \cdot E[e^{\theta X_2}] \\[5px] &= M^{X_1}(\theta) \cdot M^{X_2}(\theta) \\[5px] &= \exp [\mu_1 \theta + \dfrac{1}{2} \sigma_1^2 \theta^2] \cdot \exp [\mu_2 \theta + \dfrac{1}{2} \sigma_2^2 \theta^2] \\[5px] &= \exp [(\mu_1 + \mu_2)\theta + \dfrac{1}{2}(\sigma_1^2 + \sigma_2^2)\theta^2] \end{aligned}$$となる。
$M^{X_1 + X_2}(\theta)$は$\N(\mu_1+\mu_2, \sigma_1^2 + \sigma_2^2)$の積率母関数に一致しているため、
$$\begin{aligned} X_1 + X_2 \sim \N(\mu_1+\mu_2, \sigma_1^2 + \sigma_2^2) \end{aligned}$$が成立する。 - 確率変数$X$が正規分布に従う時、$X$を線形変換した$aX + b ~~{\small (a,bは定数)}$も正規分布に従います。
(証明)
$X \sim \N (\mu, \sigma^2)$である時、その積率母関数$M^X(\theta)= \exp [\mu \theta + \dfrac{1}{2}\sigma^2 \theta^2]$であるから、 $$\begin{aligned} M^{aX+b} (\theta) &= E[e^{\theta (aX+b)}] \\[5px] &= E[e^{a \theta X}] \cdot e^{\theta b} \\[5px] &= M^X (a \theta) \cdot e^{\theta b} \\[5px] &= \exp [\mu (a \theta) + \dfrac{1}{2}\sigma^2 (a \theta)^2] \cdot e^{\theta b} \\[5px] &= \exp [(a\mu + b)\theta + \dfrac{1}{2}(a \sigma)^2 \theta^2] \end{aligned}$$となる。
$M^{aX+b} (\theta)$は$\N(a\mu + b, a \sigma^2)$の積率母関数に一致しているため、
$$\begin{aligned} aX + b \sim \N(a \mu + b, a^2 \sigma^2) \end{aligned}$$が成立する。
3. 2変量(多変量)正規分布
(注意)
ここではベクトル・行列がたくさん出てきてadvancedなので、一旦飛ばしていただいても結構です。
以下ではまず多変量正規分布について総括し、具体例として2変量正規分布を扱います。
「確率ベクトル$\vec X (= (X_1, \ldots, X_n)^\top)$が分布パラメータ$(\vec \mu, \vec \Sigma)$の($n$変量)正規分布に従うこと」を「$\vec X \sim \N_n(\vec \mu, \vec \Sigma)$」と表します。
(ただし、$\vec \mu (= (\mu_1, \ldots, \mu_n)^\top) \in \mathbb{R^n}, \vec \Sigma$は$n \times n$正定値行列)
3-1. 確率密度関数
$$\begin{aligned} f(\vec x) = \dfrac{1}{(2 \pi)^\frac{n}{2} (\det \vec \Sigma)^{\frac{1}{2}}} \exp[- \dfrac{1}{2} (\vec x – \vec \mu)^\top \vec \Sigma^{-1} (\vec x – \vec \mu)] ~~ (\vec x \in \mathbb{R^n}) \end{aligned}$$
3-2. 特性値
$$\begin{aligned} &{\small ①平均ベクトル:}E[\vec X] = \vec \mu \\ &{\small ②分散共分散行列:}V[\vec X] (= E[(\vec X – \vec \mu)(\vec X – \vec \mu)^\top]) = \vec \Sigma \\ &{\small ③積率母関数:}M^{\vec X}(\vec \theta) = \exp [\vec \theta^\top \vec \mu + \vec \theta^\top \vec \Sigma \vec \theta \cdot \dfrac{1}{2}] \end{aligned}$$
(①〜③の証明はこちら:<補足. 連続分布_(多変量)正規分布>)
ベクトル・行列について現時点で知識不足の方は、証明をすべて追う必要はないかと思います。本質的には単変量正規分布における証明と同じことをやっているだけです。
3-3. Fig
(2変量正規分布の場合のFigです)
Fig3. 確率密度関数
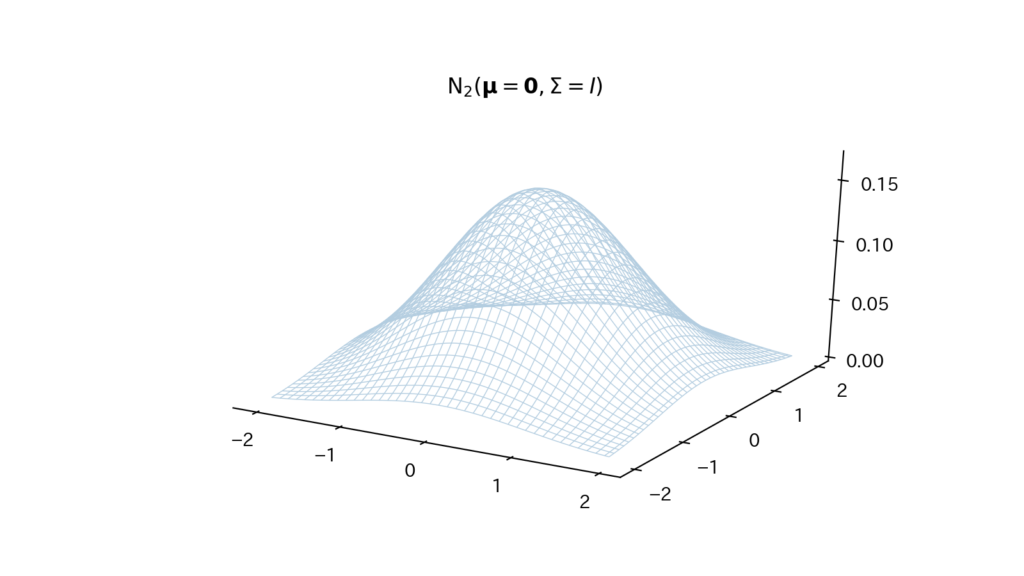
3-4. 多変量正規分布の具体例:2変量正規分布
統計検定1級には出題されるとしても$2$変量までかと思われます。
以下の例題1-3は解ける様にしておくことが望ましいです。
(例題1-3の準備)
確率ベクトル$\vec X = (X_1, X_2)^\top$、平均ベクトル$\vec \mu = (\mu_1, \mu_2)^\top$、分散共分散行列$\vec \Sigma = \begin{pmatrix} \sigma_1^2 & \rho \sigma_1 \sigma_2 \\ \rho \sigma_1 \sigma_2 & \sigma_2^2 \end{pmatrix}$とする。
この時、
$\vec \Sigma$の$(1,1)$成分である”$\sigma_1^2$”は$X_1$の分散を、
$\vec \Sigma$の$(2,2)$成分である”$\sigma_2^2$”は$X_2$の分散を、
$\vec \Sigma$の$(1,2), (2,1)$成分である”$\rho \sigma_1 \sigma_2$”は$X_1, X_2$の共分散を表します。
また、”$\rho$”は$X_1, X_2$の相関係数です。
そして多変量正規分布の記法に従うと、「確率ベクトル$\vec X$が分布パラメータ$(\vec \mu, \vec \Sigma)$の2変量正規分布に従うこと」は「$\vec X \sim \N_2(\vec \mu, \vec \Sigma)$」と表されますね。
例題1.
$\vec X \sim \N_2(\vec \mu, \vec \Sigma)$である時、確率密度関数$f(\vec x)$を$x_1, x_2, \mu_1, \mu_2, \sigma_1, \sigma_2, \rho$を用いて表せ。
解答.
$$\begin{aligned} f(\vec x) = \dfrac{1}{(2 \pi)^{\frac{2}{2}}(\det \vec \Sigma)^{\frac{1}{2}}} \exp[- \dfrac{1}{2} (\vec x – \vec \mu)^\top \vec \Sigma^{-1} (\vec x – \vec \mu)] \end{aligned}$$であるから、この右辺の要素を計算する。
まず$\det \vec \Sigma$について、
$$\begin{aligned} \det \vec \Sigma &= \det \begin{pmatrix} \sigma_1^2 & \rho \sigma_1 \sigma_2 \\[5px] \rho \sigma_1 \sigma_2 & \sigma_2^2 \end{pmatrix} \\[5px] &= \sigma_1^2 \sigma_2^2 – (\rho \sigma_1 \sigma_2)^2 \\[5px] &= (1 – \rho^2)(\sigma_1 \sigma_2)^2 \end{aligned}$$となる。
また$(\vec x – \vec \mu)^\top \vec \Sigma^{-1} (\vec x – \vec \mu)$について、
$$\begin{aligned} (\vec x – \vec \mu)^\top \vec \Sigma^{-1} (\vec x – \vec \mu) &= \begin{pmatrix}x_1 – \mu_1 & x_2 – \mu_2\end{pmatrix} \dfrac{1}{\det \vec \Sigma} \begin{pmatrix} \sigma_2^2 & -\rho \sigma_1 \sigma_2 \\ – \rho \sigma_1 \sigma_2 & \sigma_1^2 \end{pmatrix} \begin{pmatrix} x_1 – \mu_1 \\ x_2 – \mu_2 \end{pmatrix} \\[10px] &= \dfrac{1}{\det \vec \Sigma} \{ (x_1 – \mu_1)^2 \sigma_2^2 – (x_1 – \mu_1)(x_2 – \mu_2)(2 \rho \sigma_1 \sigma_2) + (x_2 – \mu_2)^2 \sigma_1^2 \} \\[10px] &= \dfrac{1}{1 – \rho^2} \{ \dfrac{(x_1 – \mu_1)^2}{\sigma_1^2} – \dfrac{2 \rho (x_1 – \mu_1) (x_2 – \mu_2)}{\sigma_1 \sigma_2} + \dfrac{(x_2 – \mu_2)^2}{\sigma_2^2} \} \end{aligned}$$となる。
よって、
$$\begin{aligned} f(\vec x) = \dfrac{1}{2 \pi \sigma_1 \sigma_2 \sqrt{1 – \rho^2}} \exp [- \dfrac{1}{2(1 – \rho^2)} \{ \dfrac{(x_1 – \mu_1)^2}{\sigma_1^2} – \dfrac{2 \rho (x_1 – \mu_1) (x_2 – \mu_2)}{\sigma_1 \sigma_2} + \dfrac{(x_2 – \mu_2)^2}{\sigma_2^2} \}] ~~~~~ \mathrm{(A)} \end{aligned}$$
- $\mathrm{(A)}$において相関係数$\rho=0$とすると、
$$\begin{aligned} f(\vec x) &= \dfrac{1}{2 \pi \sigma_1 \sigma_2} \exp [- \dfrac{1}{2} \{ (\dfrac{x_1 – \mu_1}{\sigma_1})^2 + (\dfrac{x_2 – \mu_2}{\sigma_2})^2 \}] \\ &= \dfrac{1}{\sqrt{2 \pi \sigma_1^2}} \exp [- \dfrac{(x_1 – \mu_1)^2}{2 \sigma_1^2}] \times \dfrac{1}{\sqrt{2 \pi \sigma_2^2}} \exp [- \dfrac{(x_2 – \mu_2)^2}{2 \sigma_2^2}] \end{aligned}$$と、$f(\vec x)$は$X_1, X_2$の周辺密度関数の積に変形されます。
即ち、
$$\begin{aligned} 「X_1, X_2{\small が無相関(\rho=0)}」 \Rightarrow 「X_1, X_2{\small は独立}」 \end{aligned}$$が成立します。 - (上記の補足)
一般には、「独立」→「無相関」は成立しますが、「無相関」→「独立」は成立しません。
例.
$X \sim \N(0,1), Y=X^2$である時、
$$\begin{aligned} \Cov[X,Y] &= E[(X-E[X])(Y-E[Y])] \\ &{\scriptsize (\Covの定義より)} \\[5px] &= E[X \cdot X^2] – 0 \\ &{\scriptsize (E[X]=0より)} \\[5px] &= E[X^3] \\[5px] &= \int_{- \infty}^{\infty} x^3 f(x) dx \\[5px] &= 0 \\ &{\scriptsize (x^3は奇関数、f(x)は偶関数であるため、x^3 f(x)は奇関数)} \end{aligned}$$となり、$X,Y$は無相関となる。
だが、明らかに独立ではない。
なるほどです。それにしても例題の計算が重いですね。。
しんどいですが、何とか耐えてがんばりましょう。
例題2.
(例題1からの続き)
$X_2$の周辺分布(確率密度関数)を求めよ。
解答.
$X_2$の確率密度関数$g(x_2)$を求める。
$$\begin{aligned} g(x_2) &= \int_{-\infty}^{\infty} f(\vec x) dx_1 \\[10px] &= \dfrac{1}{2 \pi \sigma_1 \sigma_2 \sqrt{1 – \rho^2}} \int_{- \infty}^{\infty} \exp [- \dfrac{1}{2(1 – \rho^2)} \{ \dfrac{(x_1 – \mu_1)^2}{\sigma_1^2} – \dfrac{2 \rho (x_1 – \mu_1) (x_2 – \mu_2)}{\sigma_1 \sigma_2} + \dfrac{(x_2 – \mu_2)^2}{\sigma_2^2} \}] dx_1 \\[10px] &= \dfrac{1}{2 \pi \sigma_1 \sigma_2 \sqrt{1 – \rho^2}} \int_{- \infty}^{\infty} \exp[- \dfrac{1}{2(1 – \rho^2)} [\{ (\dfrac{x_1 – \mu_1}{\sigma_1}) – \rho (\dfrac{x_2 – \mu_2}{\sigma_2}) \}^2 + (1 – \rho^2)(\dfrac{x_2 – \mu_2}{\sigma_2})^2]] dx_1 \\[10px] &= \dfrac{1}{2 \pi \sigma_1 \sigma_2 \sqrt{1 – \rho^2}} \exp[- \dfrac{1}{2(1 – \rho^2)}(1- \rho^2)(\dfrac{x_2 – \mu_2}{\sigma_2})^2] \cdot \int_{- \infty}^{\infty} \exp[- \dfrac{1}{2(1 – \rho^2)} \{ (\dfrac{x_1 – \mu_1}{\sigma_1}) – \rho (\dfrac{x_2 – \mu_2}{\sigma_2}) \}^2] dx_1 \\ &{\scriptsize (x_1に依存しない部分を\intの前に出した)} \\[10px] &= \dfrac{1}{\sqrt{2 \pi \sigma_2^2}} \exp [- \dfrac{(x_2 – \mu_2)^2}{2 \sigma_2^2}] \times \boldsymbol{\dfrac{1}{\sqrt{2 \pi (\sigma_1 \sqrt{1 – \rho^2})^2}} \int_{- \infty}^{\infty} \exp [- \dfrac{1}{2}(\dfrac{x_1 – \bullet}{\sigma_1 \sqrt{1 – \rho^2})^2})^2] dx_1} \\ &{\scriptsize (\bulletにx_1に関係ない項をまとめた)} \\[10px] &= \dfrac{1}{\sqrt{2 \pi \sigma_2^2}} \exp [- \dfrac{(x_2 – \mu_2)^2}{2 \sigma_2^2}] \\ &{\scriptsize (ガウス積分を用いると、太文字部分は1になる)} \end{aligned}$$
この結果は自然ですね!
例題3.
(例題1,2からの続き)
$X_2 = x_2$が与えられた時の$X_1$の条件つき分布(確率密度関数)を求めよ。
解答.
確率密度関数$f(x_1 | x_2)$を求める。
$$\begin{aligned} f(x_1 | x_2) &= \dfrac{{\small (X_1, X_2の同時密度関数)}}{{\small(X_2の周辺確率密度関数)}} \\[10px] &= \dfrac{f(\vec x)}{g(x_2)} \\[10px] &= \dfrac{\dfrac{1}{2 \pi \sigma_1 \sigma_2 \sqrt{1 – \rho^2}} \exp [- \dfrac{1}{2(1 – \rho^2)} \{ \dfrac{(x_1 – \mu_1)^2}{\sigma_1^2} – \dfrac{2 \rho (x_1 – \mu_1) (x_2 – \mu_2)}{\sigma_1 \sigma_2} + \dfrac{(x_2 – \mu_2)^2}{\sigma_2^2} \}]}{\dfrac{1}{\sqrt{2 \pi \sigma_2^2}} \exp [- \dfrac{(x_2 – \mu_2)^2}{2 \sigma_2^2}]} \\[10px] &= \dfrac{1}{\sqrt{2 \pi \sigma_1^2 (1 – \rho^2)}} \exp [- \dfrac{1}{2 (1 – \rho^2)} \{ (\dfrac{x_1 – \mu_1}{\sigma_1}) – \rho (\dfrac{x_2 – \mu_2}{\sigma_2}) \}^2] \\[10px] &= \dfrac{1}{\sqrt{2 \pi \sigma_1^2 (1 – \rho^2)}} \exp [- \dfrac{1}{2 \sigma_1^2 (1 – \rho^2)} \{ x_1 – (\mu_1 + \rho (\dfrac{\sigma_1}{\sigma_2})(x_2 – \mu_2)) \}^2] \end{aligned}$$
求めた確率密度関数の形から、
$$\begin{aligned} E[X_1 | X_2 = x_2] &= \mu_1 + \rho (\dfrac{\sigma_1}{\sigma_2})(x_2 – \mu_2) \\ V[X_1 | X_2 = x_2] &= (\sqrt{1 – \rho^2} \sigma_1)^2 \end{aligned}$$とわかります。この結果は覚えておいても良いかと思います。
4. 対数正規分布
ある確率変数$X$に対して$\log X$が正規分布に従う時、$X$は対数正規分布に従います。
「確率変数$X$が分布パラメータ$(\mu, \sigma^2)$の対数正規分布に従うこと」を
「$X \sim \LN(\mu, \sigma^2)$」と表します。(ただし、$\mu \in \mathbb{R}, \sigma^2 \gt 0$、$X$は$X \gt 0$の値をとります)
4-1. 確率密度関数
$$\begin{aligned} f(x) = \dfrac{1}{\sqrt{2 \pi \sigma^2} \boldsymbol{x}} \exp[- \dfrac{(\boldsymbol{\log x}-\mu)^2}{2 \sigma^2}] ~~ (x \gt 0) \end{aligned}$$
4-2. 特性値
$$\begin{aligned} &{\small ①平均:}E[X] = \exp [\mu + \dfrac{1}{2} \sigma^2] \\ &{\small ②分散:}V[X] = \exp [ 2 \mu + \sigma^2] \cdot \{ \exp(\sigma^2) – 1 \} \\ &{\small ③積率母関数}M^X(\theta){\small は} \theta=0 {\small まわりで(} \theta \gt 0 {\small で) 存在しません} \end{aligned}$$
(①〜③の証明はこちら:<補足. 連続分布_対数正規分布>)
4-3. Fig
Fig4. 確率密度関数
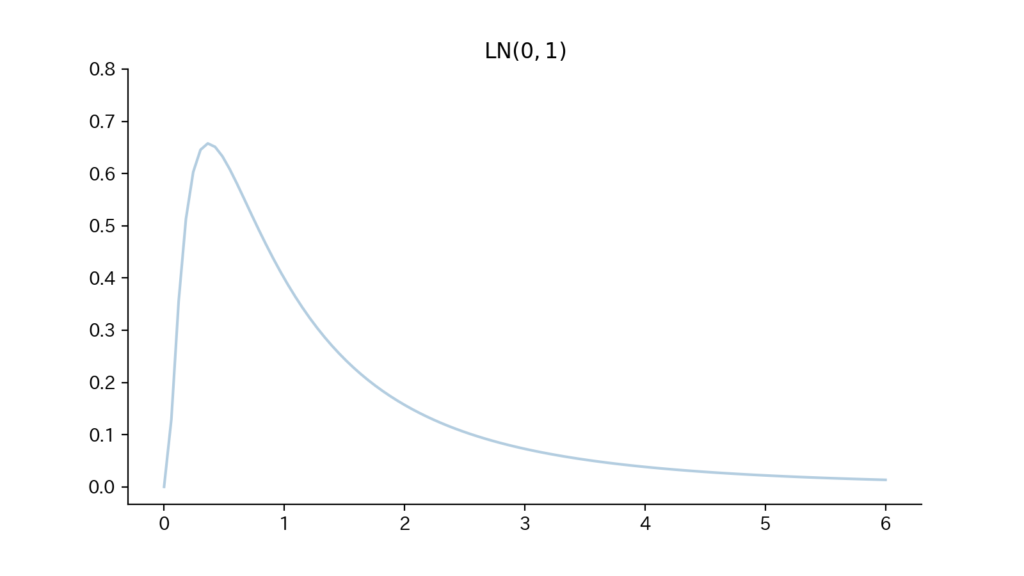
5. 混合正規分布
混合正規分布は複数の正規分布を一定割合ずつ足し合わせたものです。
「確率変数$X$が混合正規分布に従うこと」を「$X \sim \sum_{k=1}^K \pi_k \N(\mu_k, \sigma_k^2)$」と表します。また、”$\N(\mu_k, \sigma_k^2)$”を「混合要素」と言い、”$\pi_k$”を「混合比率(負担率、混合係数とも)」と言います。
(ただし、$\mu_k \in \mathbb{R}, \sigma_k^2 \gt 0, 0 \leqq \pi_k \leqq 1 ~~ {\small (k=1,\ldots,K)}, \sum_{k=1}^K \pi_k=1$)
5-1. 確率密度関数
$$\begin{aligned} f(x) = \sum_{k=1}^K \pi_k \cdot \dfrac{1}{\sqrt{2 \pi \sigma_k^2}} \exp[- \dfrac{(x-\mu_k)^2}{2 \sigma_k^2}] ~~ (- \infty \lt x \lt \infty) \end{aligned}$$
5-2. 特性値
$$\begin{aligned} &{\small ①平均:}E[X] = \sum_{k=1}^K \pi_k \mu_k \\ &{\small ②分散:}V[X] = \sum_{k=1}^K \pi_k ( \mu_k^2 + \sigma_k^2) – (\sum_{k=1}^K \pi_k \mu_k)^2 \\ &{\small ③積率母関数:}M^X(\theta) = \sum_{k=1}^K \pi_k \cdot \exp [ (\mu_k \theta + \dfrac{1}{2}\sigma_k^2 \theta^2)] \end{aligned}$$
(①〜③の証明はこちら:<補足. 連続分布_混合正規分布>)
5-3. Fig
Fig5. 確率密度関数
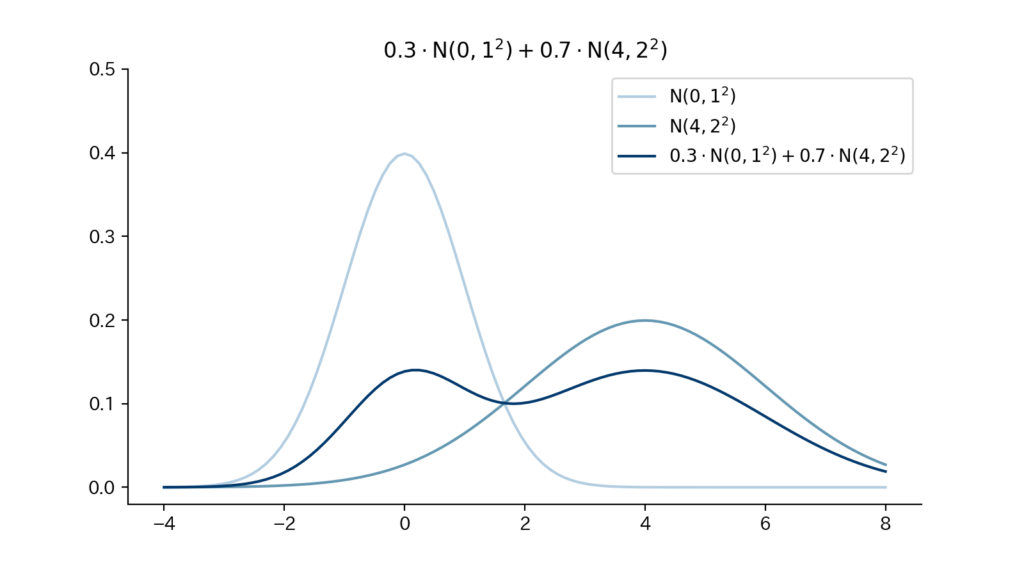
6. $\chi^2$分布
「確率変数$X$が分布パラメータ(自由度)$n {\small (\in \mathbb{N})}$の$\chi^2$分布に従うこと」を
「$X \sim \chi^2(n)$」と表します。(ただし、$X$は$X \gt 0$の値をとります)
6-1. 確率密度関数
$$\begin{aligned} f(x) = \dfrac{1}{\Gamma(\frac{n}{2}) 2^{\frac{n}{2}}} x^{\frac{n}{2} – 1} e^{- \frac{x}{2}} ~~ (x \gt 0) \end{aligned}$$
6-2. 特性値
$$\begin{aligned} &{\small ①平均:}E[X] = n \\ &{\small ②分散:}V[X] = 2n \\ &{\small ③積率母関数:}M^X(\theta) = (1 – 2 \theta)^{-\frac{n}{2}} ~~ {\small (ただし1-2\theta \gt 0)} \end{aligned}$$
(①〜③の証明はこちら:<補足. 連続分布_chi2乗分布>)
6-3. Fig
Fig6. 確率密度関数
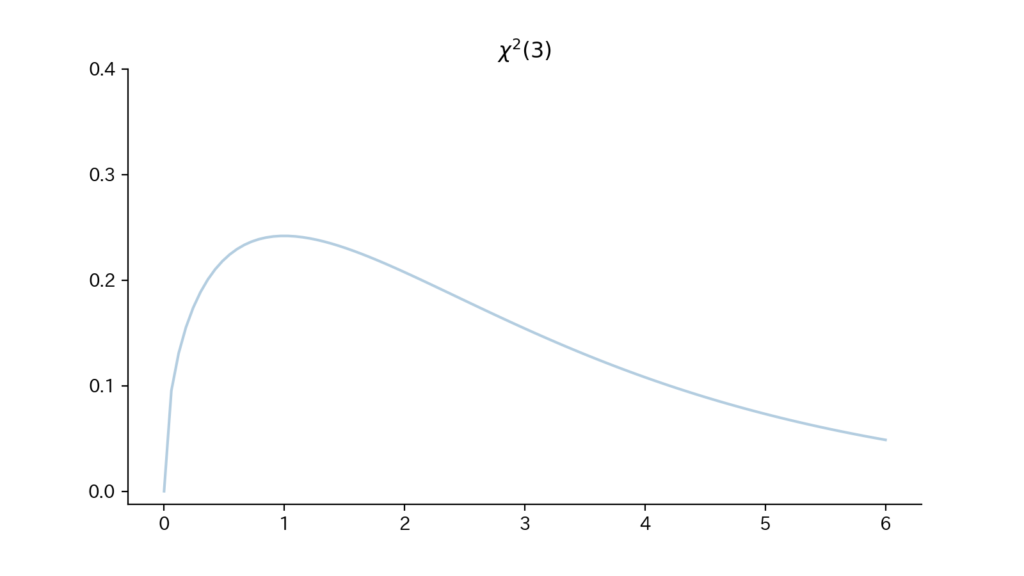
- (重要)$Z_i \overset{i.i.d}\sim \N(0,1) ~~{\small (i=1, \ldots, n)}$に対して、$X ( = \sum_{i=1}^n Z_i^2)$が従う分布が$\chi^2(n)$となります。
(証明)
積率母関数を用いて示す。ただし、$Y (\sim \chi^2(n))$の積率母関数$M^Y(\theta)$が
$M^Y(\theta) = (1-2\theta)^{-\frac{n}{2}}$であることは既知とする。
$Z_i \overset{i.i.d}\sim \N(0,1) ~~{\small (i=1, \ldots, n)}$に対して$X = \sum_{i=1}^n Z_i^2$とおくと、
$$\begin{aligned} M^X(\theta) &= E[e^{\theta X}] \\[5px] &= E[e^{\theta \sum_{i=1}^{n} Z_i^2}] \\[5px] &= \prod_{i=1}^n E[e^{\theta Z_i^2}] \\[5px] &= \{ E[e^{\theta Z_1^2}] \}^n \\ &{\scriptsize (独立性より)} \end{aligned}$$となる。
ここで$E[e^{\theta Z_1^2}]$について、
$$\begin{aligned} E[e^{\theta Z_1^2}] &= \int_{- \infty}^{\infty} e^{\theta z_1^2} \cdot {\small (\N(0,1)の確率密度関数)}dz_1 \\[10px] &= \int_{- \infty}^{\infty} e^{\theta z_1^2} \cdot \dfrac{1}{\sqrt{2 \pi}} \exp(- \dfrac{z_1^2}{2}) dz_1 \\[10px] &= \dfrac{1}{\sqrt{2 \pi}} \int_{- \infty}^{\infty} \exp(- \dfrac{1 – 2\theta}{2} z_1^2)dz_1 \\[10px] &= \dfrac{1}{\sqrt{2 \pi}} \cdot \sqrt{\frac{\pi}{(\frac{1-2\theta}{2})}} \\ &{\scriptsize (ガウス積分より)} \\[10px] &= (1-2 \theta)^{-\frac{1}{2}} \end{aligned}$$である。
よって$M^X(\theta) = (1-2 \theta)^{-\frac{n}{2}}$となり、$X, Y$の積率母関数が一致することから$X \sim \chi^2(n)$となる。 - 前述のとおり、$\chi^2$分布には再生性があります。即ち、確率変数$X_1, X_2$が互いに独立に$\chi^2$分布に従う時(注意:パラメータは異なっても構いません)、$(X_1 + X_2)$も$\chi^2$分布に従います。
(証明)
$X_1 (\sim \chi^2(n_1)), ~X_2 (\sim \chi^2(n_2))$が互いに独立である時、それぞれの積率母関数$M^{X_1}(\theta), M^{X_2}(\theta)$について、
$$\begin{aligned} M^{X_1}(\theta) &= (1-2\theta)^{- \frac{n_1}{2}} \\ M^{X_2}(\theta) &= (1-2\theta)^{- \frac{n_2}{2}} \end{aligned}$$であるから、
$$\begin{aligned} M^{X_1 + X_2}(\theta) &= E[e^{\theta (X_1 + X_2)}] \\[5px] &= E[e^{\theta X_1}] \cdot E[e^{\theta X_2}] \\[5px] &= M^{X_1}(\theta) \cdot M^{X_2}(\theta) \\[5px] &= (1 – 2\theta)^{- \frac{n_1}{2}} \cdot (1 – 2\theta)^{- \frac{n_2}{2}} \\[5px] &= (1 – 2\theta)^{- \frac{n_1+n_2}{2}} \end{aligned}$$となる。
$M^{X_1 + X_2}(\theta)$は$\chi^2(n_1+n_2)$の積率母関数に一致しているため、
$$\begin{aligned} X_1 + X_2 \sim \chi^2(n_1+n_2) \end{aligned}$$が成立する。
7. $t$分布
「確率変数$T$が分布パラメータ(自由度)$n {\small (\gt 0)}$の$t$分布に従うこと」を
「$T \sim \t(n)$」と表します。
7-1. 確率密度関数
$$\begin{aligned} f(t) = \dfrac{\Gamma(\frac{n+1}{2})}{\sqrt{\pi n} \cdot \Gamma(\frac{n}{2})} (1 + \dfrac{t^2}{n})^{-\frac{n+1}{2}} ~~ (- \infty \lt t \lt \infty) \end{aligned}$$
7-2. 特性値
$$\begin{aligned} &{\small ①平均:}E[T] = 0 ~~ {\small (ただしn \gt 1)} \\ &{\small ②分散:}V[T] = \dfrac{n}{n-2} ~~ {\small (ただしn \gt 2)} \\ &{\small ③積率母関数}M^T(\theta){\small は\theta \neq 0 で存在しません} \end{aligned}$$
(注意:$E[T] ~{\small (n=1)}, V[T] ~ {\small (n=1, 2)}$は存在しません)
(①〜③の証明はこちら:<補足. 連続分布_t分布>)
7-3. Fig
Fig7. 確率密度関数
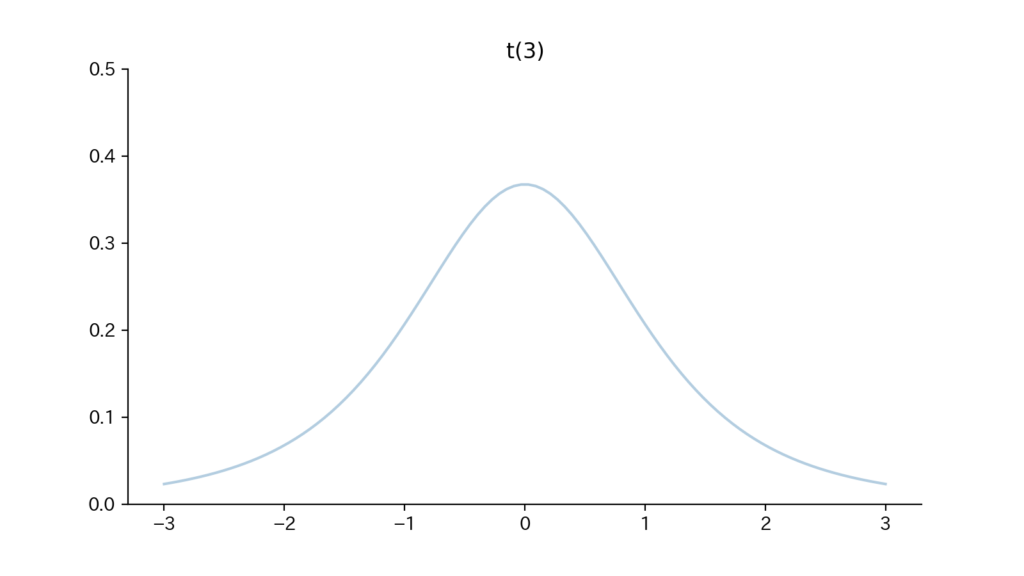
- (重要)$X (\sim \chi^2(n)), Z (\sim \N(0,1))$が互いに独立である時、$T(= \dfrac{Z}{\sqrt{\frac{X}{n}}})$が従う分布が$\t(n)$となります。
(証明)
$X, Z$の同時確率密度関数$f_{X,Z}(x,z)$は$X, Z$の独立性から互いの確率密度関数の積で表され、
$$\begin{aligned} f_{X,Z}(x,z) = (\dfrac{1}{\Gamma(\frac{n}{2})2^{\frac{n}{2}}}x^{\frac{n}{2} – 1}e^{-\frac{x}{2}}) \cdot (\dfrac{1}{\sqrt{2 \pi}}e^{-\frac{z^2}{2}}) \end{aligned}$$となる。
$\vec P = \begin{pmatrix} X \\ Z \end{pmatrix}, \vec Q = \begin{pmatrix} X^{\prime} \\ T \end{pmatrix}$として、
$$\begin{aligned} X^{\prime} &= X \\ T &= \dfrac{Z}{\sqrt{\frac{X}{n}}} \end{aligned}$$なる$1:1$の変数変換を考えると、ヤコビアン$\det J(\dfrac{\partial \vec Q}{\partial \vec P})$は、
$$\begin{aligned} \det J(\dfrac{\partial \vec Q}{\partial \vec P}) &= \det \begin{pmatrix} \dfrac{\partial x^{\prime}}{\partial x} & \dfrac{\partial x^{\prime}}{\partial z} \\[5px] \dfrac{\partial t}{\partial x} & \dfrac{\partial t}{\partial z} \end{pmatrix} \\[10px] &= \begin{pmatrix} 1 & 0 \\ \sqrt{n}z(- \dfrac{1}{2} x^{-\frac{3}{2}}) & \sqrt{n}x^{-\frac{1}{2}} \end{pmatrix} \\[10px] &= \sqrt{n}x^{-\frac{1}{2}} \end{aligned}$$となる。
よって、$X, Z$の同時確率密度関数$f_{X,Z}(x,z)$は、
$$\begin{aligned} f_{X^{\prime}, T}(x, t) &= f_{X,Z}(x, z) \cdot |\det J(\dfrac{\partial \vec Q}{\partial \vec P})| \\[10px] &= f_{X,Z}(x, z) \cdot |\dfrac{1}{\det J(\dfrac{\partial \vec P}{\partial \vec Q})}| \\ &{\scriptsize (<確率変数の変数変換>:5. おまけ. ヤコビアンの便利な性質)} \\[10px] &= (\dfrac{1}{\Gamma(\frac{n}{2})2^{\frac{n}{2}}}x^{\frac{n}{2} – 1}e^{-\frac{x}{2}}) \cdot (\dfrac{1}{\sqrt{2 \pi}}e^{-\frac{z^2}{2}}) \cdot \dfrac{1}{\sqrt{n}x^{-\frac{1}{2}}} \\[10px] &= \dfrac{1}{\Gamma(\frac{n}{2})2^{\frac{n}{2}} \cdot \sqrt{2 \pi} \cdot \sqrt{n}} \cdot x^{\prime \frac{n}{2}-1} e^{-\frac{x^{\prime}}{2}} \cdot e^{-\frac{t^2}{2}(\frac{x^{\prime}}{n})} \cdot x^{\prime \frac{1}{2}} \\ &{\scriptsize (一部を前に出してx,zにx^{\prime},tの式を代入した)} \\[10px] &= \dfrac{1}{\Gamma(\frac{n}{2}) \cdot 2^{\frac{n+1}{2}} \cdot \sqrt{\pi n}} \cdot x^{\prime \frac{n-1}{2}} \cdot \exp[-\dfrac{x^{\prime}}{2}(1 + \dfrac{t^2}{n})] \end{aligned}$$となる。(参照:<確率変数の変数変換>:5. おまけ. ヤコビアンの便利な性質)
これより、
$$\begin{aligned} {\small (Tの周辺分布)} &= \int_0^{\infty} f_{X^{\prime},T}(x^{\prime}, t) dx^{\prime} \\[10px] &= \int_0^{\infty} \dfrac{1}{\Gamma(\frac{n}{2}) \cdot 2^{\frac{n+1}{2}} \cdot \sqrt{\pi n}} \cdot x^{\prime \frac{n-1}{2}} \cdot \exp[-\dfrac{x^{\prime}}{2}(1 + \dfrac{t^2}{n})] dx^{\prime} \\[10px] &= \dfrac{1}{\Gamma(\frac{n}{2}) \cdot 2^{\frac{n+1}{2}} \cdot \sqrt{\pi n}} \cdot \int_0^{\infty} (\dfrac{2 x^{\prime\prime}}{1 + \frac{t^2}{n}})^{\frac{n-1}{2}} \cdot e^{-x^{\prime\prime}} \cdot \dfrac{2}{1+ \frac{t^2}{n}} dx^{\prime\prime} \\ &{\scriptsize (x^{\prime\prime} = \dfrac{x^{\prime}}{2} (1 + \dfrac{t^2}{n})とおいた )} \\[10px] &= \dfrac{1}{\Gamma(\frac{n}{2}) \cdot 2^{\frac{n+1}{2}} \cdot \sqrt{\pi n}} \cdot (\dfrac{2}{1 + \frac{t^2}{n}})^{\frac{n-1}{2}} \cdot (\dfrac{2}{1 + \frac{t^2}{n}}) \cdot \int_0^{\infty} x^{\prime\prime \frac{n+1}{2} – 1 } e^{-x^{\prime\prime}} dx^{\prime\prime} \\[10px] &= \dfrac{1}{\Gamma(\frac{n}{2}) \cdot \sqrt{\pi n}} \cdot (1 + \dfrac{t^2}{n})^{- \frac{n+1}{2}} \cdot \int_0^{\infty} x^{\prime\prime \frac{n+1}{2} – 1 } e^{-x^{\prime\prime}} dx^{\prime\prime} \\[10px] &=\dfrac{1}{\Gamma(\frac{n}{2}) \cdot \sqrt{\pi n}} \cdot (1 + \dfrac{t^2}{n})^{- \frac{n+1}{2}} \cdot \Gamma(\tfrac{n+1}{2}) \\ &{\scriptsize (ガンマ関数の定義より)} \\[10px] &= \dfrac{ \Gamma(\tfrac{n+1}{2}) }{\Gamma(\frac{n}{2}) \cdot \sqrt{\pi n}} \cdot (1 + \dfrac{t^2}{n})^{- \frac{n+1}{2}} \end{aligned}$$となる。これは$\t(n)$の確率密度関数と一致している。 - $\t(1)$(自由度1のt分布)は後出の「コーシー分布」であり、$\t(\infty)$(自由度$\infty$のt分布)は$\N(0,1)$(標準正規分布)となります*。
(*:正確に書くと、$\t(n) \overset{\displaystyle {d}}\longrightarrow \N(0,1)$、です)
($\t(\infty)$(自由度$\infty$のt分布)は$\N(0,1)$(標準正規分布)、の証明)
$\t(n)$の確率密度関数が$n \to \infty$で$\N(0,1)$の確率密度関数に(各$t$において)収束することを示す。 (注意:正確にはこれを示したからと言って「$\t(n) \overset{\displaystyle {d}}\longrightarrow \N(0,1)$」が示されるわけではありませんが、「$\t(n) \overset{\displaystyle {d}}\longrightarrow \N(0,1)$」は事実として成立します)
$\t(n)$の確率密度関数については、
$$\begin{aligned} {\small (t(n)の確率密度関数)} &= \dfrac{\Gamma(\frac{n+1}{2})}{\sqrt{\pi n} \cdot \Gamma(\frac{n}{2})} (1 + \dfrac{t^2}{n})^{-\frac{n+1}{2}} \\[10px] &= \dfrac{1}{\sqrt{\pi n}} \cdot \dfrac{\Gamma(\tfrac{n+1}{2} + 1)}{\frac{n+1}{2}} \cdot \dfrac{\frac{n}{2}}{\Gamma(\frac{n}{2} + 1)} \cdot (1 + \dfrac{t^2}{n})^{-\frac{n+1}{2}} \\ &{\scriptsize (一般に、\Gamma(z+1)=z \Gamma(z)、が成立しこれを2回用いた)} \\[10px] &= \dfrac{1}{\sqrt{\pi n}} \cdot \boldsymbol{\dfrac{n}{n+1} \cdot \dfrac{\Gamma(\tfrac{n+1}{2} + 1)}{\circ} \cdot \dfrac{\bullet}{\Gamma(\frac{n}{2} + 1)}} \cdot \dfrac{\overbrace{\sqrt{2 \pi (\frac{n+1}{2})} \cdot (\frac{n+1}{2})^{\frac{n+1}{2}} \cdot e^{- \frac{n+1}{2}}}^{\circ}}{\underbrace{\sqrt{2 \pi (\frac{n}{2})} \cdot (\frac{n}{2})^{\frac{n}{2}} \cdot e^{- \frac{n}{2}}}_{\bullet}} \cdot (1 + \dfrac{t^2}{n})^{-\frac{n+1}{2}} \\ &{\scriptsize (以下のスターリングの公式を利用できる形に無理やり変形した)} \end{aligned}$$と変形される。
スターリングの公式($\dfrac{\Gamma(a+1)}{\sqrt{2 \pi a} \cdot a^a e^{-a}} \overset{ a \to \infty}\longrightarrow 1$)より、上式の太字部分の$\dfrac{n}{n+1} , \dfrac{\Gamma(\tfrac{n+1}{2} + 1)}{\circ} , \dfrac{\bullet}{\Gamma(\frac{n}{2} + 1)}$はいずれも$n \to \infty$で$1$に収束するので、以下は上式の太字部分以外を考える。
$$\begin{aligned} {\small (上式の太字部分以外)} &= \dfrac{1}{\sqrt{\pi n}} \cdot \sqrt{\dfrac{n+1}{n}} \cdot \dfrac{(\frac{n+1}{2})^{\frac{n+1}{2}} \cdot e^{- \frac{n+1}{2}}}{(\frac{n}{2})^{\frac{n}{2}} \cdot e^{- \frac{n}{2}}} (1 + \dfrac{t^2}{n})^{-\frac{n+1}{2}} \\[10px] &= \dfrac{1}{\sqrt{\pi n}} \cdot \sqrt{\dfrac{n+1}{n}} \cdot \sqrt{\dfrac{n+1}{2}} \cdot (\dfrac{n+1}{n})^{\frac{n}{2}} \cdot e^{-\frac{1}{2}} \cdot (1 + \dfrac{t^2}{n})^{-\frac{n+1}{2}} \\[10px] &= \dfrac{1}{\sqrt{2 \pi}} \cdot \boldsymbol{\dfrac{1}{\sqrt{n}} \cdot \sqrt{\dfrac{n+1}{n}} \cdot \sqrt{n+1}} \cdot \underbrace{(1 + \frac{1}{n})^{\frac{n}{2}}}_{\circ} \cdot e^{-\frac{1}{2}} \cdot \underbrace{(1 + \dfrac{t^2}{n})^{-\frac{n}{2}}}_{\bullet} \cdot \boldsymbol{(1 + \dfrac{t^2}{n})^{-\frac{1}{2}}} \\[10px] &\overset{ n \to \infty}\longrightarrow \dfrac{1}{\sqrt{2 \pi}} \cdot e^{\frac{1}{2}} \cdot e^{-\frac{1}{2}} \cdot e^{- \frac{t^2}{2}} \\ &{\scriptsize (太字部分は1に、\circはe^{\frac{1}{2}}に、\bulletはe^{- \frac{t^2}{2}}に収束する)} \\[10px] &= \dfrac{1}{\sqrt{2 \pi}} e^{- \frac{t^2}{2}} \end{aligned}$$となるので題意は示された。
8. コーシー分布
コーシー分布は「自由度1の$t$分布」に相当します。
$t$分布の特殊例であり取り扱う必要性は低いですが、この分布自体が有名なので取り扱います。
8-1. 確率密度関数
$$\begin{aligned} f(x) = \dfrac{1}{\pi (1 + x^2)} ~~ (- \infty \lt x \lt \infty) \end{aligned}$$
8-2. 特性値
平均$E[X]$、分散$V[X]$、積率母関数$M^X(\theta)$はいずれも存在しません。
8-3. Fig
Fig8.
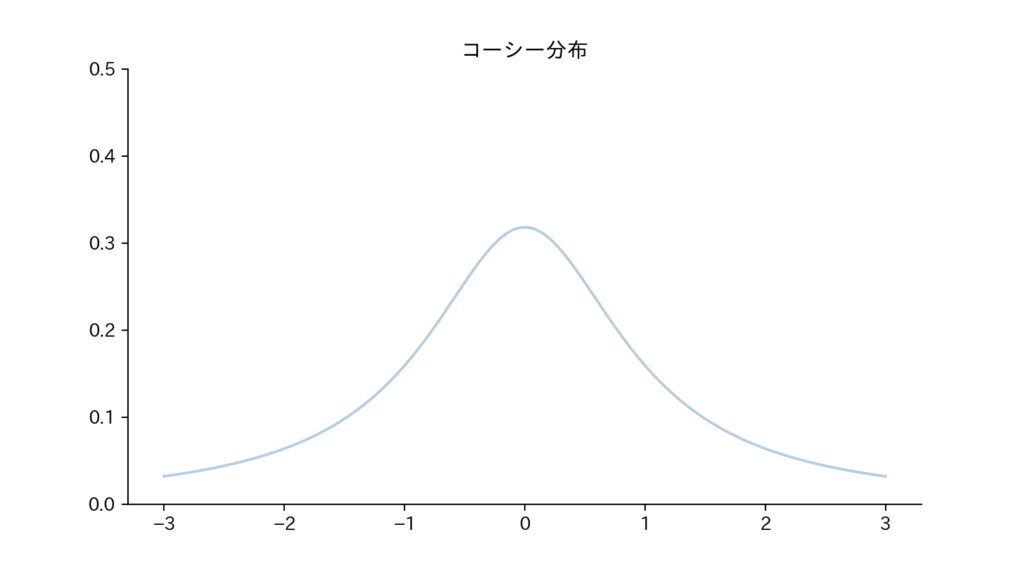
- コーシー分布で平均が存在しないことを確認してみましょう。
平均$E[X]$が存在することの定義は$E[|X|] \lt \infty$ですが、
$$\begin{aligned} E[|X|] &= \int_{-\infty}^{\infty} |x| \cdot \dfrac{1}{\pi (1 + x^2)} dx \\[10px] &= \dfrac{2}{\pi} \int_{0}^{\infty} x \cdot \dfrac{1}{1+x^2} dx \\[10px] &= \dfrac{1}{\pi} \left[ \log(1+x^2) \right]_0^{\infty} \\[10px] &= \infty \end{aligned}$$であるため、平均$E[X]$は存在しません。
(また、分散についてもその計算に平均を用いる必要があるため、存在しません) - コーシー分布で平均が存在しないことについて直感的な理解を獲得しましょう。
$$\begin{aligned} E[|X|] &= \int_{-\infty}^{\infty} \underbrace{\overbrace{|x|}^{\text{(2)}} \cdot \overbrace{\dfrac{1}{\pi (1 + x^2)}}^{\text{(3)}}}_{\text{(1)}} dx \end{aligned}$$について、$x \to \pm \infty$において$\mathrm{(1)}$は$0$に収束するもののその収束が遅いために、$E[X] = \infty$となってしまうのです。『$x \to \pm \infty$において$\mathrm{(1)}$の収束が遅い』とは、『$\mathrm{(2)}$を$\mathrm{(3)}$が抑え込む力が弱い($\mathrm{(3)}$が$x \to \pm \infty$で大きさを持ちすぎている)』とも言い換えられ、この様な分布を「すそが厚い分布」と言います。
対比として標準正規分布を考えてみると、
$$\begin{aligned} E[|X|] &= \int_{- \infty}^{\infty} \overbrace{|x|}^{(4)} \cdot \overbrace{\dfrac{1}{\sqrt{2 \pi}} e^{- \frac{x^2}{2}}}^{(5)} dx \\[10px] &= 2 \int_0^{\infty} x \cdot \dfrac{1}{\sqrt{2 \pi}} e^{- \frac{x^2}{2}} dx \\[10px] &= 2 \cdot \dfrac{1}{\sqrt{2 \pi}} \left[ – e^{- \frac{x^2}{2}} \right]_0^{\infty} \\[10px] &= \sqrt{\dfrac{2}{\pi}} \lt \infty \end{aligned}$$より平均$E[X]$は存在します。
これは、『$\mathrm{(4)}$を$\mathrm{(5)}$が抑え込む力が強い($\mathrm{(5)}$が$x \to \pm \infty$で大きさを持ちすぎていない)』ためです。
9. $\F$分布
「確率変数$X$が分布パラメータ(自由度)$(n_1, n_2)$の$F$分布に従うこと」を
「$X \sim \F(n_1, n_2)$」と表します。(ただし、$n_1, n_2 \in \mathbb{N}$、$X$は$X \gt 0$の値をとります)
9-1. 確率密度関数
$$\begin{aligned} f(x) = \dfrac{\Gamma(\frac{n_1+n_2}{2})}{\Gamma(\frac{n_1}{2}) \Gamma(\frac{n_2}{2})} \cdot \dfrac{(\frac{n_1}{n_2})^{\frac{n_1}{2}} \cdot x^{\frac{n_1}{2}-1}}{(1 + \frac{n_1}{n_2} x)^{\frac{n_1+n_2}{2}}} ~~ (x \gt 0) \end{aligned}$$
(注意:$f(x)$の中身を見ると$n_1, n_2$は対称ではないため、一般に$\F(n_1, n_2) \neq \F(n_2, n_1)$です)
9-2. 特性値
$$\begin{aligned} &{\small ①平均:}E[X] = \dfrac{n_2}{n_2 – 2} ~~ {\small (ただしn_2 \gt 2)} \\ &{\small ②分散:}V[X] = \dfrac{2 n_2^2 (n_1+n_2-2)}{n_1 (n_2-2)^2 (n_2-4)} ~~ {\small (ただしn_2 \gt 4)} \\ &{\small ③積率母関数}M^X(\theta){\small は\theta \neq 0 で存在しません} \end{aligned}$$
(①〜③の証明はこちら:<補足. 連続分布_F分布>)
9-3. Fig
Fig9.
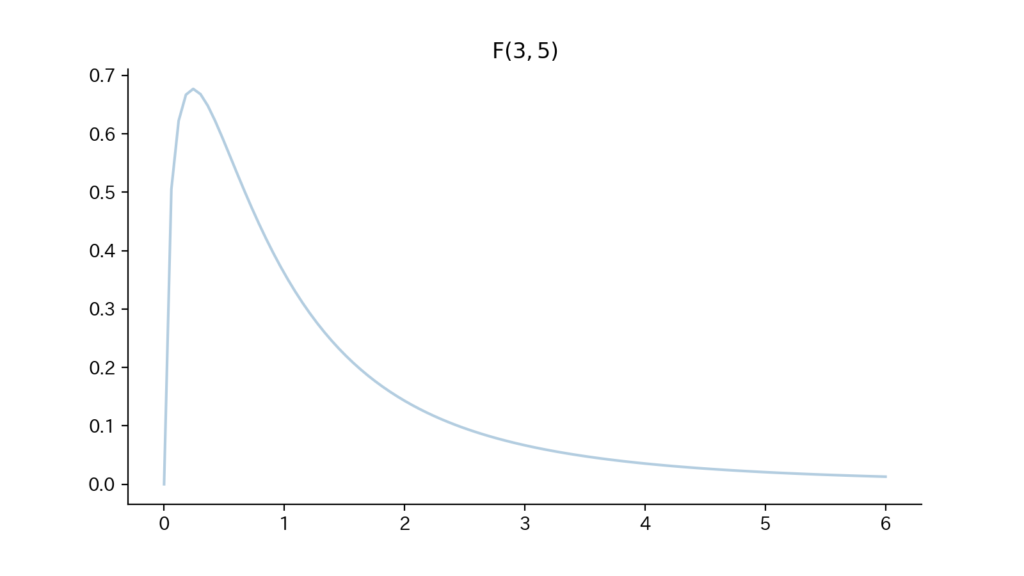
- (重要)$X_1 (\sim \chi^2(n_1)), X_2 (\sim \chi^2(n_2))$が互いに独立である時、$X = \dfrac{\frac{X_2}{n_2}}{\frac{X_1}{n_1}}$が従う分布が$\F(n_1, n_2)$となります。
(証明)
(確率変数の変数変換、周辺化の知識を用います。参照:<確率変数の変数変換>)
$X_1, X_2$の同時確率密度関数$f_{X_1,X_2}(x_1,x_2)$は$X_1, X_2$の独立性から互いの確率密度関数の積で表され、
$$\begin{aligned} f_{X_1,X_2}(x_1,x_2) &= \left\{ \dfrac{1}{\Gamma(\frac{n_1}{2}) 2^{\frac{n_1}{2}}} x_1^{\frac{n_1}{2} – 1} e^{- \frac{x_1}{2}} \right\} \cdot \left\{ \dfrac{1}{\Gamma(\frac{n_2}{2}) 2^{\frac{n_2}{2}}} x_2^{\frac{n_2}{2} – 1} e^{- \frac{x_2}{2}} \right\} \\ &= \underbrace{\dfrac{1}{\Gamma(\frac{n_1}{2}) \Gamma(\frac{n_2}{2}) 2^{\frac{n_1+n_2}{2}}}}_{\text{Cとおく}} \cdot x_1^{\frac{n_1}{2} -1} \cdot x_2^{\frac{n_2}{2} -1} \cdot e^{- \frac{x_1+x_2}{2}} \end{aligned}$$となる。
$\vec P = \begin{pmatrix} X_1 \\ X_2 \end{pmatrix}, \vec Q = \begin{pmatrix} Z \\ W \end{pmatrix}$として、
$$\begin{aligned} Z &= \dfrac{X_1}{X_2} \\ W &= X_2 \end{aligned}$$なる$1:1$の変数変換を考えると、ヤコビアン$\det J(\dfrac{\partial \vec Q}{\partial \vec P})$は、
$$\begin{aligned} \det J(\dfrac{\partial \vec Q}{\partial \vec P}) &= \det \begin{pmatrix} \dfrac{\partial z}{\partial x_1} & \dfrac{\partial z}{\partial x_2} \\[5px] \dfrac{\partial w}{\partial x_1} & \dfrac{\partial w}{\partial x_2} \end{pmatrix} \\ &= \det \begin{pmatrix} \dfrac{1}{x_2} & – \dfrac{x_1}{x_2^2} \\[5px] 0 & 1 \end{pmatrix} \\ &= \dfrac{1}{x_2} \end{aligned}$$となる。
よって$Z, W$の同時確率密度関数$f_{Z,W}(z,w)$は、
$$\begin{aligned} f_{Z,W}(z,w) &= f_{X_1, X_2}(x_1, x_2) \cdot |\det J(\dfrac{\partial \vec P}{\partial \vec Q})| \\ &{\scriptsize (<確率変数の変数変換>:5. おまけ. ヤコビアンの便利な性質)} \\[10px] &= f_{X_1, X_2}(x_1, x_2) \cdot \dfrac{1}{|\det J(\dfrac{\partial \vec Q}{\partial \vec P})|} \\[10px] &= C x_1^{\frac{n_1}{2} -1} \cdot x_2^{\frac{n_2}{2} -1} \cdot e^{- \frac{x_1+x_2}{2}} \cdot \dfrac{1}{(\dfrac{1}{x_2})} \\[10px] &= C(zw)^{\frac{n_1}{2} -1} \cdot w^{\frac{n_2}{2}} \cdot e^{-\frac{zw + w}{2}} \\[10px] &= C z^{\frac{n_1}{2} -1} \cdot w^{\frac{n_1+n_2}{2} – 1} \cdot e^{- \frac{w}{2}(z+1)} \end{aligned}$$となる。
以上より、
$$\begin{aligned} {\small (Zの周辺分布)} &= \int_0^{\infty} f_{Z,W}(z, w) dw \\[10px] &= \int_0^{\infty} C z^{\frac{n_1}{2} -1} \cdot w^{\frac{n_1+n_2}{2} – 1} \cdot e^{- \frac{w}{2}(z+1)} dw \\[10px] &= C z^{\frac{n_1}{2} -1} \cdot \int_0^{\infty} w^{\frac{n_1+n_2}{2} – 1} \cdot e^{- \frac{w}{2}(z+1)} dw \\[10px] &= C z^{\frac{n_1}{2} -1} \cdot \int_0^{\infty} (\frac{2s}{1 + z})^{\frac{n_1+n_2}{2} – 1} \cdot e^{-s} \cdot \frac{2}{1+z} ds \\ &{\scriptsize (\frac{w}{2}(z+1) = sとおいた)} \\[10px] &= C z^{\frac{n_1}{2} -1} \cdot (\frac{2}{1 + z})^{\frac{n_1+n_2}{2}} \cdot \int_0^{\infty} s^{\frac{n_1+n_2}{2} – 1} \cdot e^{-s} ds \\[10px] &= \dfrac{1}{\Gamma(\frac{n_1}{2}) \Gamma(\frac{n_2}{2}) 2^{\frac{n_1+n_2}{2}}} \cdot z^{\frac{n_1}{2} -1} \cdot (\frac{2}{1 + z})^{\frac{n_1+n_2}{2}} \cdot \Gamma(\tfrac{n_1+n_2}{2}) \\ &{\scriptsize (Cを戻し、ガンマ関数の定義を用いた)} \\[10px] &= \dfrac{\Gamma(\frac{n_1+n_2}{2})}{\Gamma(\frac{n_1}{2}) \Gamma(\frac{n_2}{2})} \cdot \dfrac{z^{\frac{n_1}{2} – 1}}{(1 + z)^{\frac{n_1 + n_2}{2}}} \end{aligned}$$となる。
最後に$Z = \dfrac{n_1}{n_2} X$と変数変換すると、
$$\begin{aligned} {\small (Xの確率密度関数)} &= {\small (Zの周辺分布)} \cdot |\dfrac{\partial z}{\partial x}| \\[10px] &= \dfrac{\Gamma(\frac{n_1+n_2}{2})}{\Gamma(\frac{n_1}{2}) \Gamma(\frac{n_2}{2})} \cdot \dfrac{(\frac{n_1}{n_2} x)^{\frac{n_1}{2} – 1}}{(1 + \frac{n_1}{n_2} x)^{\frac{n_1 + n_2}{2}}} \cdot \dfrac{n_1}{n_2} \\[10px] &= \dfrac{\Gamma(\frac{n_1+n_2}{2})}{\Gamma(\frac{n_1}{2}) \Gamma(\frac{n_2}{2})} \cdot \dfrac{(\frac{n_1}{n_2})^{\frac{n_1}{2}} \cdot x^{\frac{n_1}{2}-1}}{(1 + \frac{n_1}{n_2} x)^{\frac{n_1+n_2}{2}}} \end{aligned}$$となり、題意は示された。
10. 指数分布
「確率変数$X$が分布パラメータ$\lambda {\small (\gt 0)}$の指数分布に従うこと」を
「$X \sim \Exp(\lambda)$」と表します。(ただし、$X$は$X \gt 0$の値をとります)
10-1. 確率密度関数
$$\begin{aligned} f(x) = \lambda e^{- \lambda x} ~~ (x \gt 0) \end{aligned}$$
10-2. 特性値
$$\begin{aligned} &{\small ①平均:}E[X] = \dfrac{1}{\lambda} \\ &{\small ②分散:}V[X] = \dfrac{1}{\lambda^2} \\ &{\small ③積率母関数:}M^X(\theta) = \dfrac{\lambda}{\lambda – \theta} ~~ {\small (ただし\lambda – \theta \gt 0)} \end{aligned}$$
(①〜③の証明はこちら:<補足. 連続分布_指数分布>)
10-3. Fig
Fig10.

- 『あるイベントが1度発生してから次に発生するまでの時間』(「生起時間」)は指数分布に従うとモデリングされることがよくあります。つまり、生起時間$T$の確率密度関数$f(t)$を
$$\begin{aligned} f(t) = \lambda e^{-\lambda t} ~~ (t \gt 0) \end{aligned}$$とおきます。
この時、以下の通りになります。
$$\begin{aligned} F(t) &= \int_0^t f(s) ds \\[5px] &= \left[ -e^{-\lambda s} \right]_0^{t} \\[5px] &= 1 – e^{- \lambda t} \end{aligned}$$ $$\begin{aligned} {\small (T=tまでイベントが発生しない確率)} &= Pr\{ T \geqq t \} \\[5px] &= 1 – F(t) \\[5px] &= e^{-\lambda t} \end{aligned}$$ - (指数分布の)無記憶性:
$X \sim \Exp(\lambda)$である時、
$$\begin{aligned} Pr\{ T \geqq t + t^{\prime} | T \geqq t \} = Pr\{ T \geqq t^{\prime} \} \end{aligned}$$が成立し、これを「(指数分布の)無記憶性」と言います。
(証明)
$$\begin{aligned} Pr\{ T \geqq t + t^{\prime} | T \geqq t \} &= \dfrac{Pr\{ T \geqq t + t^{\prime} , T \geqq t \}}{Pr\{ T \geqq t \}} \\[10px] &= \dfrac{Pr\{ T \geqq t + t^{\prime} \}}{Pr\{ T \geqq t \}} \\[10px] &= \dfrac{e^{-\lambda (t + t^{\prime})}}{e^{-\lambda t}} \\[10px] &= e^{- \lambda t^{\prime}} \\[10px] &= Pr\{ T \geqq t^{\prime} \} \end{aligned}$$
無記憶性が成立するのは、連続分布においては指数分布であることを覚えておきましょう。
一方で、離散分布においては幾何分布でしたね。
11. ガンマ分布
「確率変数$X$が分布パラメータ$(a,b) ~{\small (a \gt 0, b \gt 0)}$のガンマ分布に従うこと」を「$X \sim \Ga(a, b)$」と表します。(ただし、$X$は$X \gt 0$の値をとります)
11-1. 確率密度関数
$$\begin{aligned} f(x) = \dfrac{1}{\Gamma(a) b^a} x^{a-1} e^{-\frac{x}{b}} ~~ (x \gt 0) \end{aligned}$$
(注意:$\Ga(a,b)$の”$a$”を「形状母数」と呼ばれるもので、分布の形状を決定づけます。一方の”$b$”は「尺度母数」と呼ばれるもので、分布の形状は変化させることなくスケーリングします。)
11-2. 特性値
$$\begin{aligned} &{\small ①平均:}E[X] = ab \\ &{\small ②分散:}V[X] = ab^2 \\ &{\small ③積率母関数:}M^X(\theta) = (1 – b\theta)^{-a} ~~ {\small (ただし1-b\theta \gt 0)} \end{aligned}$$
(①〜③の証明はこちら:<補足. 連続分布_ガンマ分布>)
11-3. Fig
Fig11.
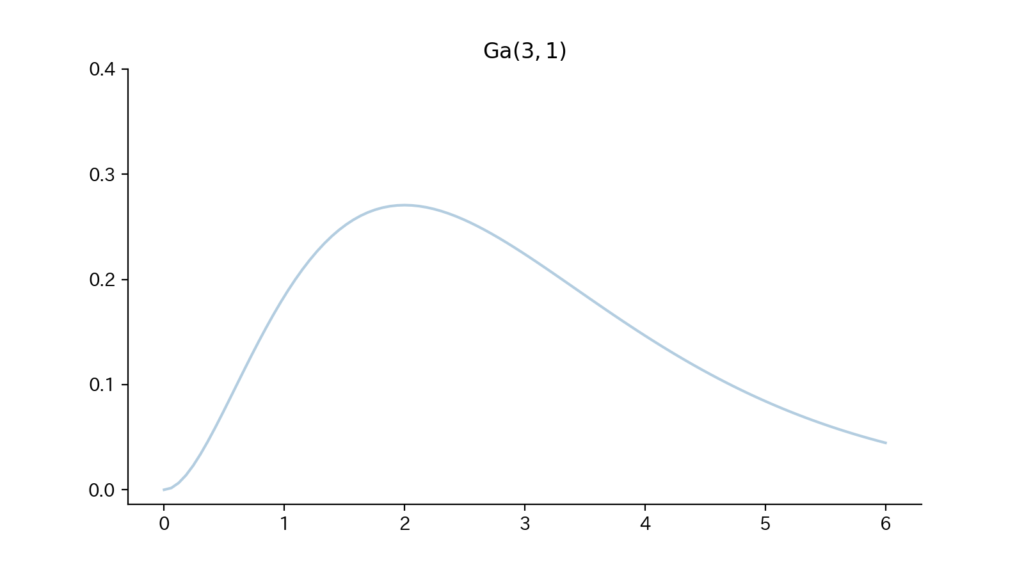
- 前述のとおり、ガンマ分布には再生性があります。即ち、確率変数$X_1, X_2$が互いに独立にガンマ分布に従う時(注意:パラメータの内、尺度母数$b$は等しい必要があります)、$(X_1 + X_2)$もガンマ分布に従います。
(証明)
$X_1 (\sim \Ga(a_1,b)), ~X_2 (\sim \Ga(a_2, b))$が互いに独立である時、それぞれの積率母関数$M^{X_1}(\theta), M^{X_2}(\theta)$について、
$$\begin{aligned} M^{X_1}(\theta) &= (1 – b\theta)^{-a_1} \\ M^{X_2}(\theta) &= (1 – b\theta)^{-a_2} \end{aligned}$$であるから、
$$\begin{aligned} M^{X_1 + X_2}(\theta) &= E[e^{\theta (X_1 + X_2)}] \\[5px] &= E[e^{\theta X_1}] \cdot E[e^{\theta X_2}] \\[5px] &= M^{X_1}(\theta) \cdot M^{X_2}(\theta) \\[5px] &= (1 – b\theta)^{-a_1} \cdot (1 – b\theta)^{-a_2} \\[5px] &= (1 – b\theta)^{-(a_1 + a_2)} \end{aligned}$$となる。
$M^{X_1 + X_2}(\theta)$は$\Ga(a_1+a_2, b)$の積率母関数に一致しているため、
$$\begin{aligned} X_1 + X_2 \sim \Ga(a_1+a_2, b) \end{aligned}$$が成立する。 - 指数分布$\Exp(\lambda)$はガンマ分布の特殊例($\Ga(1, \frac{1}{\lambda})$)とみることができます。
12. ベータ分布
「確率変数$X$が分布パラメータ$(a,b) ~{\small (a \gt 0, b \gt 0)}$のベータ分布に従うこと」を「$X \sim \Be(a, b)$」と表します。(ただし、$X$は区間$[0, 1]$の値をとります)
12-1. 確率密度関数
$$\begin{aligned} f(x) &= \dfrac{1}{B(a,b)} x^{a – 1} (1 – x)^{b – 1} ~~ (0 \lt x \lt 1) \\ &{\small (ただし、B(a,b) = \int_0^1 x^{a – 1} (1 – x)^{b – 1} dx)} \end{aligned}$$
(注意:$\Be(a,b)$の”$a$”, “$b$”を「形状母数」と呼ばれるもので、分布の形状を決定づけます。)
12-2. 特性値
$$\begin{aligned} &{\small ①平均:}E[X] = \dfrac{a}{a + b} \\ &{\small ②分散:}V[X] = \dfrac{ab}{(a + b)^2 (a + b + 1)} \\ &{\small ③積率母関数}M^X(\theta) {\small はきれいな形で書くことができないので、ここでは省きます} \end{aligned}$$
(①〜③の証明はこちら:<補足. 連続分布_ベータ分布>)
12-3. Fig
Fig12.
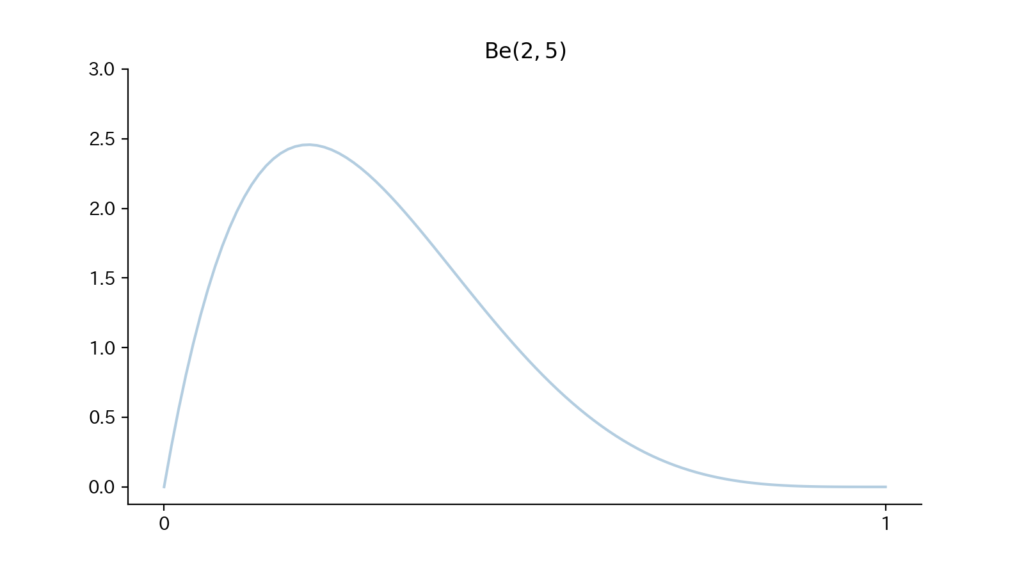
- $X_1 (\sim \Ga(a_1, b)), X_2 (\sim \Ga(a_2, b))$が互いに独立である時、$X = \dfrac{X_1}{X_1 + X_2}$が従う分布が$\Be(a_1, a_2)$となります。 (証明略)
- $\Be(1,1)$の確率密度関数は、
$$\begin{aligned} \dfrac{1}{B(1, 1)}x^{1 – 1} (1 – x)^{1 – 1} = 1 ~~ (0 \lt x \lt 1) \end{aligned}$$より、一様分布はベータ分布の特殊例($\Be(1, 1)$)とみることができます。
まとめ.
- 連続分布に属する分布間の関係性を確認し、各分布について【①確率密度関数、②特性値、③Fig】を確認した。